When I was in college, Prof. William Feller said that you should always have a concrete model with which to think about abstract math structures, and that one of the most nearly universal models was the 2-dimensional Unit Disk D1 in the complex plane C1. It is a good example of a Bounded Complex Domain, whose boundary is the unit circle S1.
When you look at the Cartesian product of two such disks, that is, the bounded complex bidisk D2 bounded complex domain in C2, you see that you have to be more careful in defining its boundary because its topological boundary is different from the most useful boundary with respect to such things as Bergman kernels, Green's functions, harmonic functions, etc. Such boundaries have been called Silov and Shilov (two different transliterations from Russian), and are also called characteristic manifolds, Bergman-Shilov boundaries, and (I think) distinguished boundaries, and perhaps other things. They are generally subsets of the topological boundaries of bounded complex domains.
The Shilov boundary of the complex bidisk is S1 x S1 , the Cartesian product of two circles. It can be described as the set (a,b) such that both a and b are on a bounding circle of one of the disks. The topological boundary of the complex bidisk is more complicated: the set (a,b) such that either a or b is on a bounding circle of one of the disks.
What the Shilov boundary is good for is that it is the minimal subset of the topological boundary over which you can integrate an analytic function to reproduce its interior values by the Poisson kernel.
Here are some references:
A good introductory paper is Conformal Theories, Curved Phase Spaces Relativistic Wavelets and the Geometry of Complex Domains, by R. Coquereaux and A. Jadczyk, Reviews in Mathematical Physics, Volume 2, No 1 (1990) 1-44, which can be downloaded from the web as a 1.98 MB pdf file.Harmonic Analysis of Functions of Several Complex Variables in the Classical Domains by Hua (Am. Math. Soc., 1979) discusses a lot of examples, but is far from introductory.
Also advanced are
Geometric Analysis on Symmetric Spaces, by Sigurdur Helgason (Am. Math. Soc., 1994), which covers Bounded Domains because they have correspondences with Symmetric Spaces;Algebraic Structures of Symmetric Domains, by Ichiro Satake (Iwanami Shoten and Princeton University Press 1980);
Analysis and Geometry on Complex Homogeneous Domains, by Jacques Faraut, Soji Kaneyuki, Adam Koranyi, Qi-keng Lu, and Guy Roos (Birkhauser 2000); and
Analysis on Symmetric Cones, by Jacques Faraut and Adam Koranyi (Clarendon Press, Oxford 1994).
Harmonic Function Theory by Axler, Bourdon, and Ramey (Springer-Verlag, 1992) is introductory, but does not do a lot of examples.
Edward Dunne has some nice WWW pages about related structures, such as Hermitian Symmetric Spaces, E8, F4, and SU(2,2).
The Shilov boundaries are used in the D4-D5-E6-E7-E8 VoDou Physics model as compact manifolds that represent spacetime, internal symmetry space, and fermion representation space.
The volumes of the manifolds are useful in calculations of particle masses and force strength constants.
Here are some of the Bounded Domains that are used in the D4-D5-E6-E7-E8 VoDou Physics model:
The manifolds RP1 x S3 and RP1 x S7 are homeomorphic to S1 x S3 and S1 x S7, which are untwisted trivial sphere bundles over S1. The corresponding twisted sphere bundles are the generalized Klein bottles Klein(1,3) Bottle and Klein(1,7) Bottle.
Note that RP1 can be described as an orbifold.
The physics of the Shilov boundaries of the Bounded Complex Domains gives us, through the D4-D5-E6-E7-E8 VoDou Physics model, Gravity and the Standard Model.
The basic useful features of compact Shilov boundaries of Bounded Complex Domains can be extended to distinguished boundaries that are non-compactly causal symmetric spaces, according to math.RT/0111033, Complex crowns of Riemannian symmetric spaces and non-compactly causal symmetric spaces, by Simon Gindikin and Bernhard Kroetz, who say:
"... we define a distinguished boundary for the complex crowns ... of non-compact Riemannian symmetric spaces G/K. The basic result is that affine symmetric spaces of G can appear as a component of this boundary if and only if they are non-compactly causal symmetric spaces. ...... The distinguished boundary is a geometrically complicated object. Usually it is a disconnected set. Nevertheless, we show that it is minimal from some analytical points of view and that it features properties expected from a Shilov boundary. ...
... it was conjectured that non-compactly causal symmetric spaces appear in the "Shilov boundary" of the complex crowns ... We establish this conjecture (in a more exact form); namely we prove:
Theorem B. If one of the components G=Hj ... in the "Shilov boundary" of the complex crown ... is a symmetric space, then it is a non-compactly causal symmetric space. Moreover, every non-compactly causal symmetric space occurs as a component of the distinguished boundary of some complex crown ...Let us say a few words about the motivation of this conjecture. On Riemannian symmetric spaces we have an elliptic analysis and on non-compactly causal symmetric spaces we have a hyperbolic analysis. It is known in mathematical physics that in many important cases elliptic and hyperbolic theories can be "connected" through complex domains (Laplacians and wave equations, Euclidean and Minkowski field theories etc). Theorem B implies a connection of Riemannian and non-compactly causal symmetric spaces through the complex crowns ... It shows that the phenomenon described above has a non-trivial generalization to symmetric spaces. ...".
Such complex crowns are further described in math.RT/0110173, also by Simon Gindikin and Bernhard Kroetz.
Since the Unit Disk D1, the Poincare Disk, is the simplest Bounded Complex Domain, to get some intuition about what happens in the Interior, look at the Interior of D1.
Another reason that D1 is a useful model is that its Shilov boundary is the circle S1, and the 4-dim and 8-dim SpaceTimes in the D4-D5-E6-E7-E8 VoDou Physics model are the Shilov boundaries of bounded compex domain, which Shilov boundaries are, respectively, RP1 x S3 and RP1 x S7, and S1 is topologically RP1, so that:
Note that S1/Z2 can be described as an orbifold.
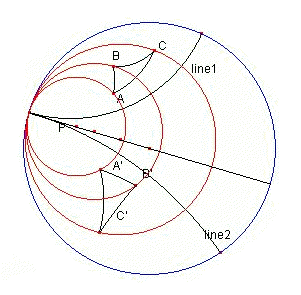
The image below, of the Poincare disk, is modified from an image on the isometries page of the Hyperbolic Geometry web pages of Tim Lister.

The outer blue circle is the boundary of the Unit Disk (for which the Shilov boundary and topological boundary coincide) and the lines of the Poincare Hyperbolic Geometry are the circle arcs within the boundary that are perpendicular to the boundary where they intersect it.
From each point on the boundary, there are a infinite number of lines such as the black lines line1, line2, and the diameter line. Since they all intersect only at the given boundary point, which is at infinity in the Poincare Hyperbolic Geometry, those lines are called the pencils of parallel lines from the given boundary point.
Note that there are some lines from different boundary points may not intersect with each other at all, not even at infinity. Such lines are called ultraparallel.
Consider the pencil of parallel lines from the given boundary point. The circles that are perpendicular to all the parallel lines in the pencil are all tangent to the given boundary point, and form an orthogonal family of circles called horocycles. Three horocycles are shown in red, and their centers, as well as the center of the Unit Disk itself, are shown as red points. They all fall on the diameter line of the pencil of parallel lines from the given boundary point.
The triangle A'B'C' is a translation of triangle ABC, with the translation being produced by two reflections by two of the parallel lines in the pencil of parallel lines from the given boundary point.
The horocycles at the given boundary point are the paths of parabolic translation isometries of the Unit Disk generated by reflections by the parallel lines in the pencil of parallel lines from the given boundary point.
4-dim Physical Shilov Boundary SpaceTime 8-dim Shilov Boundary SpaceTime
8-real-dim Complex Physical SpaceTime 16-real-dim Complex SpaceTime
1 - Merging Physical SpaceTime
with Internal Symmetry Space, to get a HyperSpace of Internal Symmetry Space.
This occurs at energies above the quark/hadron phase transition and in a 173 GeV Truth Quark - Planck Energy Vacuum excited state. This gives the Eighth Dimension of Buckaroo Banzai:
"... matter is comprised mostly of empty space; subatomic particles ...[are]... like ... bee[s] in the middle of St. Peter's Cathedral ... the 8th Dimension ... is ... to be found in the subatomic realm ... In the Kaluza-Klein theory, ... lines become cylinders with a radius much less than that of an atomic nucleus. ... each dimension of spacetime is in fact two-dimensional ... There would then be a total of eight dimensions, in which the eighth dimension is the sister dimension of everyday time, but at the subnuclear level. ... Why can't we perceive all eight dimensions like Buckaroo Banzai? Because when we move along a mini-dimension, we are moving around the perimeter of the cylinder, which instantaneously leads us back to where we started. In other words, we move through eight dimensions all the time, but we just don't know we've made the trip because it was so short! Therefore, we don't have time to perceive it. ... The key to the door of matter ... lies in the poorly understood mechanism of "spontaneous symmetry breaking," ... the beam produces a small region of high energy density ...[a Plank Energy Vacuum excited state with 8-dimensional Spacetime]... It had been B. Banzai's contention ... that consciousness was a particle-wave akin to light ... broadcast ... in the manner of a radio transmitter ... most humans are aware of receiving fuzzy signals of alien consciousness from other worlds, other dimensions, but for reasons of psychological resistance or biological limitation cannot interpret them clearly ... In effect, our so-called sophisticated brains are obsolescent radio sets with ...[poor]... tuners. ... If consciousness ...[could be tuned accurately]... the entire bandwidth of consciousness would become clear. ...".
2 - Going from the Shilov Boundary Physical SpaceTime
into the Interior of its Bounded Complex Domain, to get a HyperSpace of Complex SpaceTime.
since a pencil of parallel lines connects any given boundary point to every other boundary point, if you use the Interior of the Bounded Domain,
In that view, Complex SpaceTime HyperSpace corresponds to the MacroSpace of Many-Worlds of Bohm-Many-Worlds Quantum Theory. What would be required for physical travel through that HyperSpace?
Note that all horocycles at a given boundary point are isomorphic (by flow along the parallel lines in the pencil at the point) to the entire boundary, which in the D1 case is also the Shilov boundary. Maybe you would only need a minimal amount of energy to just get off the Shilov boundary and into the Interior, after which travel would be easy. (Compare the stargate of the disk in the ring of a Kerr-Newman Black Hole.)
What would be required for communication through that HyperSpace?
Consider a configuration, such as a Quantum Consciousness pattern of thought, at a given point in SpaceTime (Point in space and time in Time).Could another configuration, at another point in SpaceTime (Point in space and time in Time), have a resonant connection with the given configuration?
If so:
Could you have a resonant connection with yourself at another time of your life?Could you have a resonant connection with another like-minded being of another time or place?
Could such resonant connections help you in dealing with Fate?
The Poisson Kernel determines any analyic function in a Bounded Domain in terms of an integral over its values on the Shilov boundary of the Bounded Domain.
The Bergman Kernel determines any analyic function in a Bounded Domain in terms of an integral over its values on the Bounded Domain itself.
From the Bergman Kernel, you can define a Riemannian metric and a Laplace-Beltrami operator. The Lapacian can also be derived, for spin manifolds, from the Dirac operator.
From the Laplace-Beltrami operator you can get Harmonic functions and Green's functions.
In the particular example of the Unit Disk D1, the Riemannian measure and the differential operators associated with the Laplace-Beltrami operator are invariant under the isometries of D1, which isometries are complex conjugation plus (denoting complex conjugation by *) the maps
which maps form the group
so that, since SO(2) fixes the origin o of D1, D1 can be identified with SU(1,1) / SO(2).
Note that D1, the simple basic example of a Bounded Complex Domain, has structure of the Lie group SU(1,1), which is the noncompact version of the compact Lie group SU(2) = Spin(3) = Sp(1) = S3, which is in some sense the basic building block of the other compact nonabelian semi-simple Lie groups.

The (4,8) hyperbolic tesselation, in which 4-sided squares meet 8 at a vertx, shown above is from the other tessellations page of the Hyperbolic Tesselations part of a website of David E. Joyce.
A hyperbolic tesselation in which 3 triangles and 3 squares are at a vertex is the basis of M. C. Escher's Circle Limit III, shown as scanned from The World of M. C. Escher, New Concise NAL Edition, Abrams 1971:

Compare the Spherical Geometry of the cuboctahedron,
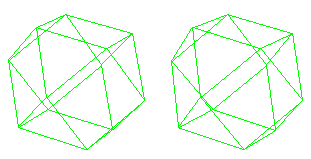
in which 2 triangles and 2 squares are at each vertex.
The book The Eightfold Way: The Beauty of Klein's Quartic Curve, edited by Silvio Levy (MSRI Publications -- Volume 35, Cambridge University Press, Cambridge, 1999) describes the roots of the
which has the symmetry group PSL(2,7). To represent the roots, Felix Klein constructed the Klein Configuration:

The Klein Configuration is related to:
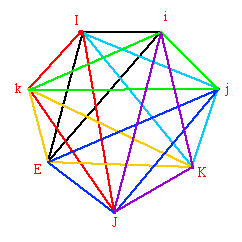
Felix Klein was primarily interested in group theory and projective geometry, and did not realize when he wrote his Order-Seven paper in 1878-1879 that his Klein Configuration could be extended to fill up the Lobachevskii plane. Therefore, it was Poincare who realized how to extend the Klein Configuration to fill up the Lobachevkii plane by making a Poincare disk. It was not until 1882 that Klein, during a sleepless night, really understood what Poincare had done. Only then was Klein able to formulate his stuff on automorphic functions etc.
The Klein Configuration represents the group SL(2,7) with 336 elements, each element represented by a triangle. The Klein Configuration has a central 14-gon, and so 14 slices. Each slice has 24 triangles.
SL(2,7) is not a simple group. It is the double cover of the Klein Quartic symmetry group PSL(2,7). PSL(2,7) is simple and has 168 elements, which are represented by the colored triangles of the Klein Configuration. Each of the14 slices of the Klein Configuration has 12 colored triangles. The colored triangles can be grouped in groups of 7, each group forming one of 24 heptagons:
The 24-heptagon Klein Configuration corresponds to a genus-3 Riemann Surface that looks somewhat like a fat tetrahedron covered by 24 tiles.
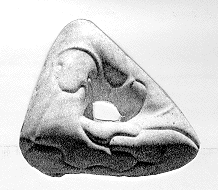
It looks somewhat like the 4th-order Roman surface of Steiner whose equation is
except that the Klein Configuration has 3 holes with nothing at its center, while the Roman surface of Steiner has a central point, like a heptahedron / onarhedron.
PSL(2,7) acting on Complex Projective 2-space CP2 has structure:
Subgroup Order Orbit Order
1 168
2 84
3 56
4 42
6 28
7 24
8 21
12 no fixed point
21 no fixed point
24 no fixed point
168 no fixed point
The 168-element group PSL(2,7) of the Klein Configuration is isomorphic to the symmetry group SL(3,2) of the Fano plane that describes Octonion multiplication.
The automorphism group of the octonions is 14-dimensional G2.
Therefore:
Here are some more interesting things:
The Poincare Disk can be identified with SU(1,1) / SO(2).
SU(1,1) = SL(2,R) contains SL(2,Z)
As John Conway says in The Sensual Quadratic Form (MAA 1997):
"... GL(2,Z) consists of all the symmetries,
while SL(2,Z) consists only of the "rotational" ones ...
... PGL(2,Z) is the full symmetry group of a packing
of the hyperbolic plane by ... horocycles ...
There is one horocycle for each rational number p/q and
it touches the boundary (... the real axis ...) at p/q. ...".
SL(2,7) is a discrete subgroup of SL(2,Z) based on prime 7 (like Z7).
SL(2,7) is the Klein 336 that double-covers the PSL(2,7) Klein 168
and they give the Klein 14-gon.
Therefore,
the Klein 14-gon corresponds to a discrete subgroup of SU(1,1),
and so corresponds
to the 14 Lobachevskii triangles of the Klein configuration.
According to the book Singularities of Differentiable Maps, Volume I, by V. I. Arnold, S. M. Gusein-Zade, A. N. Varchenko (Birkhauser 1985):
Such singularities may be useful in describing Branching of the Worlds of the Many-Worlds, related to 26-dimensional Bosonic String Theory and a 27-dimensional M-Theory.
Here are some more details based on
Arnold's paper Uspekhi. Mat. Nauk 30:5 (1975) 3-65,
or Russian Math. Surveys 30:5 (1975) 1-75,
but expanded by some of my speculations:
Consider the following table:
Unimodal Exceptional Dolgachev Numbers Gabrielov Numbers
1-Parameter Families
Q10 2 3 9 3 3 4
Q11 2 4 7 3 3 5
Q12 3 3 6 3 3 6
S11 2 5 6 3 4 4
S12 3 4 5 3 4 5
U12 4 4 4 4 4 4
Z11 2 3 8 2 4 5
Z12 2 4 6 2 4 6
Z13 3 3 5 2 4 7
W12 2 5 5 2 5 5
W13 3 4 4 2 5 6
E12 2 3 7 2 3 7
E13 2 4 5 2 3 8
E14 3 3 4 2 3 9
Note that the following 6 of the 14 have Dolgachev = Gabrielov,
and they are the ones with subscript 12:
Unimodal Exceptional Dolgachev Numbers Gabrielov Numbers 1-Parameter Families Q12 3 3 6 3 3 6 S12 3 4 5 3 4 5 U12 4 4 4 4 4 4 Z12 2 4 6 2 4 6 W12 2 5 5 2 5 5 E12 2 3 7 2 3 7
Note that the following 4 pairs of the 14
have Dolgachev (of one) = Gabrielov (of the other):
Unimodal Exceptional Dolgachev Numbers Gabrielov Numbers
1-Parameter Families
Q10 2 3 9 3 3 4
E14 3 3 4 2 3 9
Q11 2 4 7 3 3 5
Z13 3 3 5 2 4 7
S11 2 5 6 3 4 4
W13 3 4 4 2 5 6
Z11 2 3 8 2 4 5
E13 2 4 5 2 3 8
This 6+8 split of the 14 corresponds to the fibration of the Lie Group G2:
G2 / SU(3) = S6 (the 6-sphere)
To see how G2 decomposes under that fibration,
look at the G2 root vector diagram
from the point of view of a 24-cell
with the perspective having a central 14-vertex rhombic docedahedron:
with central 14-vertex rhombic dodecahedron
The 6 blue vertices correspond to the S6 of the fibration of G2,
and
the 8 red vertices correspond to the SU(3) of the fibration of G2,
with the 2 red vertices connected by the black line corresponding
to the 2-dimensional Cartan subalgebra of G2.
From the point of view of the cuboctahedral perspective of the 24-cell,
the 12 vertices of the central cuboctahedron correspond
to the 12 vertices of the G2 root vector diagram
(not including the origin / Cartan subalgebra):
The 6 blue vertices correspond to the S6 of the fibration of G2,
and
the 6 red vertices (not at the origin / Cartan subalgebra)
correspond to the 6 root vectors of the SU(3) of the fibration of G2.
When the 3-dimensional figure is projected into 2-dimensional space,
you get
the root vector diagram of G2.
The 8 of the 4 pairs Q10-E14, Q11-Z13, S11-W13, and Z11-E13
correspond to the 8 generators of the SU(3) subgroup of G2:
Q10-E14 corresponds to the 2-dim Cartan subalgebra,
and
Q11-Z13, S11-W13, and Z11-E13 correspond to the opposite-pairs
of the Mogen David root vector diagram of SU(3) in the diagram below:
/\
____/__\____
\ / \ /
\/ \/
/\ /\
/__\____/__\
\ /
\/
While the Dolgachev Numbers are based on discrete subgroups of SU(1,1)
(compare the MacKay correspondence based on discrete subgroups of SU(2))
the Gabrielov Numbers are based on quadratic forms of singularities.
Arnold, mentioning a remark by D. B. Fuks, says
"... the sum of all six Gabrielov and Dolgachev numbers
of each of the fourteen singularities is equal to 24. ..."
and Arnold goes on to say
"... the singularities that are dual to each other are precisely those
for which the Coxeter numbers ... coincide. ...
... At the present stage
the theory of singularities is an experimental science. ...".
24, the sum of Gabrielov and Dolgachev numbers,
is an interesting number, being:
the dimension of the Leech lattice,
the number of vertices of a 24-cell, and
the number of heptagons in the Klein Configuration.
Further,
the sum of all Gabrielov and Dolgachev numbers for all 14 is
14 x 24 = 336, the dimension of SL(2,7) which is
the double-cover of PSL(2,7) with 168 elements.
The fact that the sum of Gabrielov and Dolgachev numbers is 24 may be related to their duality within the 24-dimenisonal lattice denoted K24 by Wolfgang Ebeling in alg-geom/9612010,
in which he says:
"... the even unimodular lattice
K24 = (-E8) + (-E8) + U + U + U + U
of rank 24 ...
can be considered as the full homology lattice of a K3 surface,
K24 = H0(S,Z) + H2(S,Z) + H4(S,Z)
where the inner product on H0(S,Z) + H4(S,Z) is defined in such a way
that this lattice corresponds to a unimodular hyperbolic plane U. ...
The lattice K24 has the same rank as the Leech lattice,
but contrary to the Leech lattice
it is indefinite and has signature (4,20) ...".
Note that in the D4-D5-E6-E7-E8 VoDou Physics model,
the sum of the dimensions of spacetime
and fermion particle representation space
and fermion antiparticle representation space is:
prior to spacetime dimensional reduction, 8+8+8 = 24;
after spacetime dimensional reduction, 4+8+8 = 20.
K3 surfaces are related to attempts to find something
that has a complex structure that looks like S4,
which does not have a complex structure.
I understand such a complex structure to be roughly
a globally consistent set of coordinates that have complex structure.
S2, the Riemann sphere, has such a set of coordinates,
but no other even-dimensional sphere does,
although S6 has "almost complex" structure
related to a 6-dim subspace of 8-dimensional octonions,
and
the product of spheres S1 x Sk for k = 2n - 1 has complex structure.
S4 has real homology
1
0
0
0
1
K3 has complex homology
1
0 0
1 20 1
0 0
1
that is, non-zero homology in the 0=(0,0)-homology
and 4=(2,2)-homology, just like S4,
and
has zero homology in the 1=((1,0)+(0,1))-homology
and 3=((2,1)+(1,2))-homology, also just like S4,
but
has non-zero homology in the 2=((2,0)+(1,1)+(0,2))-homology, unlike S4.
Since the 2-homology measures things like 2-spheres,
K3 has a lot (22 in fact) of different "S2-type structures"
and
S4 does not have any such "S2-type structures".
Such erroneous terminology still exists on my web site, with respect to, for example, Spin(7) / G2.
The book Einstein Manifolds by Besse (Springer 1987) lists (on page 203) SO(7) / G2 as a compact non-symmetric strongly isotropy irreducible space, and on pages 179-180 it is stated that Spin(7) / G2 and S7 are related by Spin(7) acting transitively on S7 with isotropy subgroup K and a 0-dimensional "space of G-invariant Riemannian metrics up to homotheties (i.e., isometries and multiplication by a positive constant)."and that "... G2 [subgroup of] SO(7) ... G2 ...[is]... NOT the full group of isometries of any Riemannian metric on the corresponding sphere [S7]. We recall that any SO(n)-invariant metric on S(n-1) is (proportional to) the canonical one, so the full group of isometries is O(n). Thus even SO(n) is not the full group of isometries of any Riemannian metric on S(n-1). ...".
Joseph A. Wolf, in his book Spaces of Constant Curvature (5th ed) (Publish or Perish 1984), says (at page 302): "... Added in proof. A completes structure theory and classification [
] has now been worked out for the isotropy irreducible riemannian manifolds. Unfortunately it is too long and technical to summarize here. ...".
The book Clifford Algebras and the Classical Groups by Ian Porteous (Cambridge 1995) describes the structure G2 -> Spin(7) -> S7 in terms of exact sequences and coset spaces.
Hua Type I(p,q) domain to Type AIII rank=min(p,q) space SU(p+q) / S(U(p)xU(q)) It is of tube type for p = q .
Its Shilov boundary is determined by the condition U U*' = I (where * denotes conjugate and ' denotes transpose and I is the pxp identity matrix).Hua Type II(n) (EDM Type III(n)) domain to Type CI rank=n space Sp(n) / U(n) It is of tube type.
It has real dimension p ( 2q - p ).
Its Shilov boundary is determined by the condition U U* = I, so it is the symmetric unitary matrices of order n.
It has real dimension n ( n + 1 ) / 2.
Hua Type III(n) (EDM Type II(n)) domain to Type DIII rank=[n/2] space Spin(2n) / U(n) It is of tube type for even n.
Its Shilov boundary is, for even n, the skew-symmetric unitary matrices of order n
(for odd n, the definition is a bit more complicated).
According to page 7 of Hua it has real dimension n ( n - 1 ) / 2 + ( 1 + (-1)^n ) ( n - 1 ) / 2
but
I think that is a typographical error and
the real dimension should be n ( n - 1 ) / 2 + ( 1 - (-1)^n ) ( n - 1 ) / 2
Here is why:
Spin(2,6) / Spin(2)xSpin(6) has real dimension 28 - 1 - 15 = 12 and complex dimension 12/2 = 6
and its Shilov boundary has real dimension 12/2 = 6.
Spin*(8) / U(4) has real dimension 28 - 16 = 12 and complex dimension 12/2 = 6
and its Shilov boundary has real dimension with the corrected formula 4x3/2 + (1-1)x3/2 = 6
which is consistent with the isomorphisms:
Spin(2,6 ) = Spin*(8) and Spin(2)xSpin(6) = U(4).
Hua
Type
IV(n) (p=2) domain to Type BDI rank=2 space Spin(n+2)
/
Spin(n)xU(1) It is of tube type.
The Type IV(n) domain, related to Graded Lie Algebras I6 and I15, is used in the D4-D5-E6-E7-E8 VoDou Physics model. It is the Lie sphere that consists of all n-dimensional complex vectors z such
that | z z' |^2 + 1 - 2 z z' > 0 and | z z' | < 1 (where z' denotes the tranpose of z),
and
its Shilov boundary consists of vectors of the formexp( i theta ) x ( where 0 < theta < pi and x is a real n-dim vector such that x x' = 1 ). That is, the Shilov boundary of Spin(n+2) / Spin(n)xU(1) is RP1 x S(n-1) (where S(n-1) is the (n-1)-sphere in n-dim space). It has real dimension n.
In Analysis and Geometry on Complex Homogeneous Domains, by Jacques Faraut, Soji Kaneyuki, Adam Koranyi, Qi-keng Lu, and Guy Roos (Birkhauser 2000), Soji Kaneyuki says (at pages 105-106, 127, 130-131): "... By a symmetric R-space we mean a compact irreducible Hermitian symmetric space or a real form (i.e., the set of fixed points by an involutive anti-holomorphic isometry) of it. The class of symmetric R-spaces contains the Shilov boundaries of bounded symmetric domains of tube type. ... For an irreducible symmetric domain of tube type with dimension greater than 1, we show the coincidence of the causal automorphism group of the Shilov boundary and the full holomorphic automorphism group of the domain. ... The Shilov boundary of an irreducible bounded symmetric domain is a flag manifold of the 1st kind or of the 2nd kind, according as the domain is of tube type or not. ... Symmetric R-spaces [include] ... Shilov type (the Shilov boundaries of irreducible bounded symmetric domains of the tube type); ...
- Q_2,q+1(R) = S1 x Sq ... ".
In Algebraic Structures of Symmetric Domains, by Ichiro Satake (Iwanami Shoten and Princeton University Press 1980), Ichiro Satake says (at pages 128, 116-118): "... given data ( U, V, W, H ), where U is a vector space over R of dimension m (>0) and V is a vector space over C of dimension n ... W is a (non-degenerate) open convex cone in U (with vertex at the origin) and H is a hermitian map VxV -> Uc (C-linear in the second variable and C-antilinear in the first). ... assume that H is W-positive ... H(v,v) in W - {0} for all v in V, v=/= 0. Then by definition the Siegel domain S = S(U,V,W,H) is given by
S = { (u,v) in Uc x V | Im(u) - H(v,v) in W } ... When V = {0}, we obtain a "tube domain"
S = U + iW = { u in Uc | Im(u) in W }, which is also called a Siegel domain of the first kind. In general, any Siegel domain (of the second kind) S(U,V,W,H) contains a tube domain U + iW as the zero section { v = 0 }. ... Any Siegel domain is holomorphically equivalent to a bounded domain. ...
... in the following list ... dimensions of G, V, U are to be understood as the real one, while dim D is always the complex one. The symbol ~ stands for an isogeny. ...
IV(p) G = SO(p,2) (P>3). r = 2, dim G = (1/2)(p+1)(p+2), dim D = p ...
For b = 2 ... Gk(1) = {1}, Gk(2) = R* x SO(p-1,1) ...dim V = 0, dim U = p. ...".
For n = 4, Spin(6) / Spin(4) x U(1),
the Shilov boundary is RP1 x S3, which corresponds in the D4-D5-E6-E7-E8 VoDou Physics model to Physical SpaceTime after Dimensional Reduction. The 3 dimensions of the S3 correspond to the 3 imaginary quaternions.
For n = 8, Spin(10) / Spin(8) x U(1),
the Shilov boundary is RP1 x S7, which corresponds in the D4-D5-E6-E7-E8 VoDou Physics model to SpaceTime prior to Dimensional Reduction. The 7 dimensions of the S7 correspond to the 7 imaginary octonions.
Type IV(4) domains have been used to understand physics by Coquereaux and Jadczyk. An example of their line of thinking is given by the following quote from the paper by R. Coquereaux entitled Lie Balls and Relativistic Quantum Fields, Nuc. Phys. B. 18B (1990) 48-52:
"... In the present paper, we are mainly interested in the four dimensional (complex) Lie ball that we shall denote by D. This smooth manifold can be written as SOo(4,2) / SO(4)xSO(2) or as SU(2,2) / S(U(2)xU(2)). ... D is a bounded non compact symmetric domain of type I and IV. ... The metric of D is euclidean and blows up near the boundary (as in the usual geometry of Lobachevski) but ... induces a conformal Lorentz structure on the boundary. The domain D is a Lie ball ... the Shilov boundary (compactified Minkowski Space-Time) can be defined as the Lie sphere ... The domain D also admits an unbounded realization: the future tube. ... This last unbounded realization of the Lie ball admits a simple physical interpretation. ... the imaginary part y of z = x + iy can be interpreted as the inverse of a momentum ... Points of the domain D describe therefore both the position (in space and time) and the momentum (with p^2 > 0) associated with a physical event. The domain itself becomes therefore a curved relativistic phase-space. Interpretation of Im(z) as an inverse momentum is an obvious four-dimensional generalization of what is done in usual wavelet analyisis (where the variable v in z = t + i/v is interpreted as a frequency). ...".
Two other papers with similar approach are:
and
BORN'S RECIPROCITY IN THE CONFORMAL DOMAIN, by ARKADIUSZ JADCZYK, in Z. Oziewicz et al. (eds.) Spinors, Twistors, Clifford Algebras and Quantum Deformations, 129-140. (Kluwer Academic Publishers 1993)
Type V exceptional domain to Type EIII rank=2 space E6 / Spin(10)xU(1)
The Type V domain,related to Graded Lie Algebras I9, I10, I17, e7, e8, and e26; and g(ev) types e7, e8, and e26; is of the Type EIII space is used in the D4-D5-E6-E7-E8 VoDou Physics model in describing the representation space of the 8 first generation fermion particles and their 8 antiparticles. It has 78-45-1 = 32 real dimensions, and corresponds to the full spinor representation of Spin(10).
It has 16-complex dimensions, and is the complexified octonion projective plane (CxO)P2.
In Exceptional Lie Algebras and the Structure of Hermitian Symmetric Spaces, by Daniel Drucker (AMS 1978), Daniel Drucker gives "... a description of the noncompact dual of E7 / E6xSO(2) as a bounded domain in the vector space J3(CxO) ...[the complexification of the 27-dimensional exceptional Jordan algebra J3(O)] ... despite its lower dimension, the 16[complex]-dimensional [exceptional domain] is more complicated [than the 27[complex]-dimensional exceptional domain] ...this stems from the fact that the 16[complex]-dimensional domain [of the noncompact dual of E6 / SO(10)xSO(2)] (unlike the 27-dimensional domain) is not of tube type. ... The [16-complex-dimensional] noncompact dual of E6 / SO(10)xSO(2) is described as a bounded domain in a subspace of J3(CxO) ... M. Ise obtained a realization of the form ...[of elements of]... a in CxO + CxO ... The element a in CxO + CxO determines a transformation of J3(CxO) ... whose matrix ... [can be written as] ...
0 z1 0
A = 0 0 z2
0 0 0... The bounded realizatioins of the noncompact dual of E6 / SO(10)xSO(2) obtained by ... Ise ... [is] ... the same as the realization obtained from the Tits construction [as a bounded domain in the vector space J3(CxO)] ...".
In Analysis and Geometry on Complex Homogeneous Domains, by Jacques Faraut, Soji Kaneyuki, Adam Koranyi, Qi-keng Lu, and Guy Roos (Birkhauser 2000), Soji Kaneyuki says (at pages 113, 127, 124, 160, 174-176): "... a semisimple GLA [Graded Lie Algebra] has the form
g = SUM(-v < k < +v) g(k) with g(-v) =/= 0. Such a GLA is called a GLA of the v-th kind. ... the pair (Z,t) is the associated pair, where Z is the characteristic element and t is a grade-reversing Cartan involution. ... Let g ... be a real simple GLA of the v-th kind, and (Z,t) be the associated pair. Let Go be the group of grade-preserving automorphisms of G. ... Let U = Go exp(g(1) + ... + g(v)), which is a parabolic subgroup of G. The real flag manifold M = G/U is called a flag manifold of the v-th kind. ... The Shilov boundary of an irreducible bounded symmetric domain is a flag manifold of the 1st kind or of the 2nd kind, according as the domain is of tube type or not. ... EXCEPTIONAL SIMPLE GLA'S OF THE SECOND KIND [include] ...
(e7) g = E6(-14), II = BC2, II1 = {gamma2},
- g(0) = so(1,7) + R + iR, [gauge bosons in VoDou Physics]
- dim g(-1) = 16, [fermion particles + antiparticles in VoDou Physics]
- dim g(-2) = 8, [spacetime + internal symmetry space in VoDou Physics]
... The element I lies in g(0), and ad(I) gives a complex structure on g(-1). Thus g(-1) is C-linearly isomorphic to g~+(-1) ...[where ~ denotes a complex GLA of the 2nd kind, sort of a complexification of g, whose characteristic element is Z0]... consider the two graded subalgebras of Cg:
g_ev = g(-2) + g(0) + g(2) , g' = g(-2) + g'(0) + g(2) ,
where g'(0) = [ g(-2) , g(2) ] . Let n = { X in g(0) : [ X , g(-2) ] = 0 } ...
g(0) = g'(0) + n (direct sum) ... ... g_ev for ... simple GLA of the 2nd kind ...[include]...
(e7) ( E6(-14), so(2,8) + iR ) ... Let M = G/Go be the simple reducible pseudo-Hermitian symmetric space associated with a complex simple GLA ... the root system delta(g,c) is either of type BCr or Cr, where r is the split rank of M. ... the minimal dimensional G-orbit Mr is flag manifold of the 2nd kind ... [if] ... delta(g,c) is of type BCr ... Let Er be the isotropy subgroup of G ... Let er = LieEr ...
er = g~((-2) + g~(-1) + g(0) , if delta(g,c) is of type BCr ... Er = C(Z,Z0) exp(g~(-2) + g~(-1)) , if delta(g,c) is of type BCr ...
where C(Z,Z0) is the centralizer of the two elements Z and Z0 in G. ... G = C(Z,Z0) Ad(g) ... a ... simple reducible pseudo-Hermitian symmetric space of type BCr and the corresponding minimal dimensional boundary orbits Mr ...[is]...
M = EC6 / Spin(10,C) C* , Mr = E6 / Spin(8) T2 , r = 3.
[where T2 = S1 x S1 = U(1) x U(1)] ...".
The structure of M3 = E6 / Spin(8) T2 is an important mathematical structure in VoDou Physics. In particular, the non-tube-type Type V exceptional domain has a Shilov boundary that is a flag manifold of the 2nd kind, corresponding to its 2-graded GLA, in which:
- grade 0 corresponds to gauge bosons in VoDou Physics.
- grades +/- 1 correspond to fermion particles + antiparticles in VoDou Physics.
- grades +/- 2 correspond to spacetime + internal symmetry space in VoDou Physics.
In math.CV/9905183, Wilhelm Kaup and Dmitri Zaitsev say (about E6 / SO(10)xU(1): "... the exceptional bounded symmetric domain of [ complex ] dimension 16... non-compact type E III ... has rank 2 and the Shilov boundary S: = S2 has CR-dimension 8 and CR-codimension 8. On S the group Spin(10) acts transitively and the reduction ... of S is the symmetric Hermitian manifold SO(10) / (SO(2) x SO(8)), the complex nonsingular quadric of dimension 8. The group AutCR(S) is a non-compact simple exceptional real Lie group of type E6 and has dimension 78. ...". They say that the EIII domain is NOT a tube-type domain, and that "... the Shilov boundary of a bounded symmetric domain of tube type is totally real ...".
In Algebraic Structures of Symmetric Domains, by Ichiro Satake (Iwanami Shoten and Princeton University Press 1980), Ichiro Satake says (at pages 128, 116-118): "... given data ( U, V, W, H ), where U is a vector space over R of dimension m (>0) and V is a vector space over C of dimension n ... W is a (non-degenerate) open convex cone in U (with vertex at the origin) and H is a hermitian map VxV -> Uc (C-linear in the second variable and C-antilinear in the first). ... assume that H is W-positive ... H(v,v) in W - {0} for all v in V, v=/= 0. Then by definition the Siegel domain S = S(U,V,W,H) is given by
S = { (u,v) in Uc x V | Im(u) - H(v,v) in W } ... When V = {0}, we obtain a "tube domain"
S = U + iW = { u in Uc | Im(u) in W }, which is also called a Siegel domain of the first kind. In general, any Siegel domain (of the second kind) S(U,V,W,H) contains a tube domain U + iW as the zero section { v = 0 }. ... Any Siegel domain is holomorphically equivalent to a bounded domain. ...
... in the following list ... dimensions of G, V, U are to be understood as the real one, while dim D is always the complex one. The symbol ~ stands for an isogeny. ...
(V) G = (2E6,2) (K ~ Spin(10) x SO(2)), r = 2, dim G = 78, dim D = 16 ...
For b = 2 ... Gk(1) = C(1), V(1) = C, rho(1) = id,Gk(2) ~ R* x Spin(7,1), V(2) = C8, rho(2) = spin,dim V = 16 (C-type), dim U = 8. ...".
In Analysis and Geometry on Complex Homogeneous Domains, by Jacques Faraut, Soji Kaneyuki, Adam Koranyi, Qi-keng Lu, and Guy Roos (Birkhauser 2000), Adam Koranyi says (at page 218): "... S_T = ... = K_T / L_T is a (real) Riemannian symmetric space. In the tube type case this is the whole Bergman-Shilov boundary. In the general case S is a fiber space over K / K_T with fiber S_T. ...".
Adam Koranyi and Joseph A.Wolf, in Ann. Math. 81 (1965) 265-288, say (at pages 275-277): "... 4.9 Theorem. Let S be the Bergman-Shilov boundary of M = [ G0 / K ] = G0(x) [ embedded as the lower hemisphere ] in M*; let L and L1 be the isotropy subgroups of K and K1 at c(x). Then:
- 1. S = K(c(x) = K / L and dim S = dim p2 + (1/2) dim p1 > (1/2) dim M.
- 2. K(c2(x)) is a totally geodesic complex submaifold of M*, and is thus a compact hermitian symmetric space; the isotropy subgroup of K at c2(x) is the analytic subgroup K' with Lie algebra k', so K(c2(x)) = K / K'.
- 3. The map k(c(x)) -> k(c2(x)) is a fibering of S over K(c2(x)); the fibre over k(c2(x)) is k(K1(c(x))), which is totally geodesic in M*, riemanian symmetric and isometric to K1 / L.
- 4. The following statements are equivalent:
- (i) Z is in a three-dimensional simple subalgebra.
- (ii) the Cayley transform c has order 4, i.e., g = g1.
- (iii) S is a totally geodesic submanifold of M*, so S is riemannian symmetric and the largest connected group of isometries consists of the motions induced by K.
- (iv) The dimension of S is half of the real dimension of M.
- (v) K(c2(x)) is a single point. ...
... 4.10 Example. Let M be the open unit ball in complex euclidean space Cn. Then [ its compact dual space ] M* is the complex projective space CPn ... S [ the Shilov boundary ] is the full topological boundary S(2n-1) of M [ embedded as the lower hemisphere ] in M*, K(c2(x)) is the polar hyperplane CP(n-1) to x in M*, and the fibering S -> K(c2(x)) is the usual circle bundle S(2n-1) -> CP(n-1). ...".
Joseph A. Wolf, in his article Fine Structure of Hermitian Symmetric Spaces, in the book Symmetric Spaces (ed. by Boothby and Weiss, Marcel Dekker 1972), says (at page 292): "... Classification of Boundary Components. ... of an irreducible Hermitian symmetric space of noncompact type and rank r. For each integer m, 0 < m < r, there is just one G0-equivalence class { Xm,0 } of boundary component of symmetric space rank m ... X0,0 is a single point, and the Xm,0 are given by ... X0 = Xr,0 ...
X0 = E6 / SO(10)xSO(2); here r = 2 and X1,0 is the open unit ball in C5. ...".
If, for this non-tube case of Type V,
the base space of the fibration is regarded as the full topological boundary S9 of the open unit ball in C5, which S9 has the circle fibration S1 -> S9 -> CP4, and
the real fiber is regarded as S1xS7
then the Shilov boundary for EIII may be regarded as being a bundle made up of S1xS7, S1, and CP4.
Here I regard the Shilov boundary for EIII as a bundle with fibre S1xS7 and base space S9 with its own fibration S1 -> S9 -> CP4.
The Shilov boundary fibre S1xS7 is real Riemannian symmetric space.
The structure of CP4 is related to the structure of Twistors, and that CP4 has a totally geodesic embedding of CP4 in the quadric Q8 in CP9 in C10.
CP4 = CP0 u CP1 u CP2 u CP3 u C4 , and the unit sphere in C4 is the 7-sphere S7, so that the Shilov boundary base space bundle S1 -> S9 -> CP4 contains an S1xS7 that is isomorphic to the fibre S1xS7 and has complex structure related to the CP4. The complex structure of E6 can be seen by considering the 78-45-1 = 32-real-dimensional complexified Octonion projective plane (CxO)P2 = E6 / (Spin(0,10) x U(1)).
Since S1 = RP1, each S1xS7 is isomorphic to the Shilov boundary for SO(10) / SO(8)xU(1), which is the Lie sphere RP1 x S7.
In the D4-D5-E6-E7-E8 VoDou Physics model:
- the representation space for the 8 first-generation fermion particles would correspond to the Shilov boundary real fibre Lie sphere RP1 x S7;
- the representation space for the 8 first-generation fermion anti-particles would correspond to the Shilov boundary base manifold S1xS7 = RP1xS7, with the base manifold S7 being embedded in the CP4 of the Shilov boundary base space bundle S1 -> S9 -> CP4.
Type VI exceptional domain to Type EVII rank=3 space E7 / E6xU(1) It is of tube type.
The Type VI domain,related to Graded Lie Algebras I11, I12, and I18, is used in the D4-D5-E6-E7-E8 VoDou Physics model in describing the MacroSpace of the Many-Worlds. It has 133-78-1 = 54 real dimensions. The 54 = 2x27 dimensions correspond to a complexification of a 27-dimensional bosonic string M-theory that could represent Timelike Brane Universes.
In math.RA/0001083, C.H. Barton and A. Sudbery say: "... most exceptional Lie algebras are related to the exceptional Jordan algebra of 3 x 3 hermitian matrices with entries from the octonions, O. ... this relation yields descriptions of certain real forms of the complex Lie algebras
- F4 ... which can be interpreted as octonionic versions of ... the Lie algebra of antihermitian 3 x 3 matrices ...
- E6 ... which can be interpreted as octonionic versions of ... the Lie algebra of .... special linear 3 x 3 matrices and ...
- E7 which can be interpreted as octonionic versions of ... the Lie algebra of ... symplectic 6 x 6 matrices. ...".
In Exceptional Lie Algebras and the Structure of Hermitian Symmetric Spaces, by Daniel Drucker (AMS 1978), Daniel Drucker gives "... a description of the noncompact dual of E7 / E6xSO(2) as a bounded domain in the vector space J3(CxO) ...[the complexification of the exceptional Jordan algebra J3(O)] ...".
From another point of view, the Symmetric Space E7 / E6xU(1) can be represented as the 2x27 = 54-real dimensional Complexification of the Jordan algebra J4(Q)o = J3(O).
In math.CV/9905183, Wilhelm Kaup and Dmitri Zaitsev say that E7 / E6xU(1) and SO(n+2) / SO(n)xU(1) give tube-type domains, and that "... the Shilov boundary of a bounded symmetric domain of tube type is totally real ...".
In Algebraic Structures of Symmetric Domains, by Ichiro Satake (Iwanami Shoten and Princeton University Press 1980), Ichiro Satake says (at pages 128, 116-118): "... given data ( U, V, W, H ), where U is a vector space over R of dimension m (>0) and V is a vector space over C of dimension n ... W is a (non-degenerate) open convex cone in U (with vertex at the origin) and H is a hermitian map VxV -> Uc (C-linear in the second variable and C-antilinear in the first). ... assume that H is W-positive ... H(v,v) in W - {0} for all v in V, v=/= 0. Then by definition the Siegel domain S = S(U,V,W,H) is given by
S = { (u,v) in Uc x V | Im(u) - H(v,v) in W } ... When V = {0}, we obtain a "tube domain"
S = U + iW = { u in Uc | Im(u) in W }, which is also called a Siegel domain of the first kind. In general, any Siegel domain (of the second kind) S(U,V,W,H) contains a tube domain U + iW as the zero section { v = 0 }. ... Any Siegel domain is holomorphically equivalent to a bounded domain. ...
... in the following list ... dimensions of G, V, U are to be understood as the real one, while dim D is always the complex one. The symbol ~ stands for an isogeny. ...
(VI) G = (E7,3) (K ~ (E6) x SO(2)), r = 3, dim G = 133, dim D = 27 ...
For b = 3 ... Gk(1) = {1}, Gk(2) ~ R* x (E6,2),dim V = 0, dim U = 27 ( U = H3(O) ). ...".
In Analysis and Geometry on Complex Homogeneous Domains, by Jacques Faraut, Soji Kaneyuki, Adam Koranyi, Qi-keng Lu, and Guy Roos (Birkhauser 2000), Soji Kaneyuki says (at pages 105-106, 127, 130-131): "... By a symmetric R-space we mean a compact irreducible Hermitian symmetric space or a real form (i.e., the set of fixed points by an involutive anti-holomorphic isometry) of it. The class of symmetric R-spaces contains the Shilov boundaries of bounded symmetric domains of tube type. ... For an irreducible symmetric domain of tube type with dimension greater than 1, we show the coincidence of the causal automorphism group of the Shilov boundary and the full holomorphic automorphism group of the domain. ... The Shilov boundary of an irreducible bounded symmetric domain is a flag manifold of the 1st kind or of the 2nd kind, according as the domain is of tube type or not. ... Symmetric R-spaces [include] ... Shilov type (the Shilov boundaries of irreducible bounded symmetric domains of the tube type); ...
- Q_2,q+1(R) = S1 x Sq ,
- T . E6 / F4 ... ".
Note that S1 x Sq is the Lie sphere RP1 x S(n-1) Shilov boundary for SO(n+2) / SO(n)xU(1).
Since the 1-torus T is the 1-sphere S1, and since E6 / F4 is the traceless 26-dimensional Jordan subalgebra J3(O)o, you can write the Shilov boundary of the Type VI domain of the type EVII space E7 / E6xU(1) as
S1 x J3(O)o . In the D4-D5-E6-E7-E8 VoDou Physics model, the Shilov boundary (1+26)=27-dimensional S1 x J3(O)o may represent a 27-dimensional bosonic M-theory of the MacroSpace of the Many-Worlds.
The S1 x J3(O)o Shilov boundary can be considered to be an imaginary quaternification of the Shilov boundary for SO(10) / SO(8)xU(1), or in other words an imaginary quaternification of the Lie sphere RP1 x S7, with real dimension 8+8+8 = 24, plus an SU(2) (imaginary quaternions) that can be represented by the 3-sphere S3, for a total of 24 + 3 = 27 real dimensions.
This structure is consistent with the quaternionic structure of E7 as can be seen by considering the quaternionified Octonion projective plane, which is the 133-66-3 = 64-real-dimensional space (QxO)P2 = E7 / (Spin(0,12) x SU(2)).
Since each of the imaginary quaternions has the same signature (unlike the real 1 and imaginary i of the complex numbers), the 27-real-dimensional Shilov boundary could be a totally real part of the boundary of the 27-complex-dimensional domain of Type EVII corresponding to E7 / E6xU(1).
In the image, the 3-sphere S3 is represented by 3 of the 4 Clifford-Hopf circles of the 24-cell. ( I apologize that my illustration above can be seen on close inspection to be technically inaccurate since its interlocking red, blue, and green circles have the linking of Borromean Rings instead of Clifford-Hopf circles. ) The 27-dimensionality of the Shilov boundary corresponds to the 27-dimensionality of the exceptional Jordan algebra J3(O).
Could it represent structure in the MacroSpace of the Many-Worlds that is related to the Type EIX rank=4 space E8 / E7xSU(2) ?
Amassa Fauntleroy has written a paper, math.AG/0104112, Projective Ranks of Compact Hermitian Symmetric Spaces, whose abstract states:
"Let M be a compact irreducible Hermitian symmetric space and write M=G/K, with G the group of holomorphic isometries of M and K the stability group of the point of 0 in M.We determine the maximal dimension of a complex projective space embedded in M as a totally geodesic submanifold."
Type AI rank=(n-1) space SU(n) / Spin(n)Type AII rank=(n-1) space SU(2n) / Sp(n)
Type BDI rank=min(p,q) space Spin(p+q) / Spin(q)xSpin(q) for (p,q =/= 2)
Type CII rank=min(p,q) space Sp(p+q) / Sp(q)xSp(q)
Type EI rank=6 space E6 / Sp(4)
Type EII rank=4 space E6 / SU(6)xSU(2)
This 78-52 = 26 dimensional symmetric space is the set of OP2 in (CxO)P2, and corresponds to the traceless 26-dimensional Jordan subalgebra J3(O)o of the 27-dimensional exceptional Jordan algebra J3(O), and to the 26-dimensional representation of F4.The 26 dimensions correspond to a 26-dimensional bosonic String Theory that could represent the Bohm Potential of the Many-Worlds Quantum Theory.
In Analysis and Geometry on Complex Homogeneous Domains, by Jacques Faraut, Soji Kaneyuki, Adam Koranyi, Qi-keng Lu, and Guy Roos (Birkhauser 2000), Soji Kaneyuki says (at pages 139-141) [Here I use J(3)(O) etc instead of the notations H(3)(O) etc used in the quoted work.]: "... open orbits ... and their coset space expressions ...[that]... are what Koecher calls omega-domains ...[include]...
(I11) { X in J3(O') : N(X) > 0 }, { X in J3(O') : N(X) < 0 },
where N denotes the reduced norm of J3(O'). Both are expressed as R+ x E6(6) / F4(4) ...(I12) J(3-i,i)(O), i - 0,1,2,3.
- J(3,0)(O) and J(0,3)(O) are expressed as R+ x E6(-26) / F4
- J(2,1)(O) and J(1,2)(O) are expressed as R+ x E6(-26) / F4(-20) ...
(I18) { X in J3(O)^C : N(X) =/= 0 } = C* x E6^C / F4^C ,
where N denotes the reduced norm of the Jordan algebra J3(O)^C ...".
In math.RA/0001083, C.H. Barton and A. Sudbery say: "... most exceptional Lie algebras are related to the exceptional Jordan algebra of 3 x 3 hermitian matrices with entries from the octonions, O. ... this relation yields descriptions of certain real forms of the complex Lie algebras
- F4 ... which can be interpreted as octonionic versions of ... the Lie algebra of antihermitian 3 x 3 matrices ...
- E6 ... which can be interpreted as octonionic versions of ... the Lie algebra of .... special linear 3 x 3 matrices and ...
- E7 which can be interpreted as octonionic versions of ... the Lie algebra of ... symplectic 6 x 6 matrices. ...".
E6 can be considered to be made up of two representations of F4:
- the 52-dimensional adjoint representation, which corresponds to
plus
- the minimal non-trivial 26-dimensional representation, which corresponds to the non-Shilov Boundary Complex Parts of
- 8-complex-dimensional D5/D4xU(1); and
- 16=8+8-complex-dimensional E6/D5xU(1),
so that
E6 / F4 corresponds to the Complex Part of E6 in the D4-D5-E6-E7-E8 VoDou Physics model, and
F4 corresponds to the D4+Shilov Boundaries Part.
The D4+Shilov Boundaries Part of E6 represents gauge bosons, spacetime plus internal symmetry space, and fermions;
The Complex Part of E6 represents the possibilities of the Many-Worlds, through its role in the Shilov Boundary for E7 / E6xU(1), that describes the MacroSpace of the Many-Worlds.
Type EV rank=7 space E7 / SU(8)
Type EVI rank=4 space E7 / Spin(12)xSU(2)
This 133-66-3 = 64 dimensional symmetric space is the quateroctonionic projective plane (QxO)P2, and corresponds to the full spinor representation of Spin(12).Type EVIII rank=8 space E8 / Spin(16)
This 248-120 = 128 dimensional symmetric space is the octooctonionic projective plane (OxO)P2, and corresponds to a half-spinor representation of Spin(16).Type EIX rank=4 space E8 / E7xSU(2)
This 248-133-3 = 112 dimensional symmetric space,related to Graded Lie Algebras e16, e18, and e30; and g(ev) types e16, e18, and e30; is used in the D4-D5-E6-E7-E8 VoDou Physics model in describing the Algebraic and Geometric Structure of the MacroSpace of the Many-Worlds, with the 112 = 4x28 dimensions corresponding to a quaternification of a 28-dimensional bosonic string F-theory that could represent Spacelike Brane Universes.
The image shows the 112 dimensions as a total quaternification of the Shilov boundary for E7 / E6xU(1), that is, 4 of those 27-dimensional Shilov boundaries, plus for 3 of the 4 a 3-sphere S3 represented by the 3 + 1 fundamental tori of its Hopf Fibration. ( I apologize that my illustration above can be seen on close inspection to be technically inaccurate since its interlocking red, blue, and green circles have the linking of Borromean Rings instead of Clifford-Hopf circles. )
Each of the four 27-dimensional components corresponds to the 27-dimensionality of the exceptional Jordan algebra J3(O), and each combined with its corresponding Clifford-Hopf circle represents a copy of the 28-dimensional Jordan algebra J4(Q).
Type FI rank=4 space F4 / Sp(3)xSU(2)
Type FII rank=1 space F4 / Spin(9)
This 52-36 = 16 dimensional symmetric space is the octonionic projective plane OP2, and corresponds to the spinor representation of Spin(9).Type G rank=2 space G2 / Spin(4)
Here is another list, with some descriptions of further properties.
References: See Encyclopedic Dictionary of Mathematics, second edition, MIT Press 1993; Hua, Harmonic Analysis of Functions of Several Complex Variables in the Classical Domainsm Am. Math. Soc. 1979; Helgason, Differential Geometry, Lie Groups, and Symmetric Spaces, Academic 1978; Helgason, Groups and Geometric Analysis, Academic 1984; Besse, Einstein Manifolds, Springer-Verlag 1987; Rosenfeld, Geometry of Lie Groups, Kluwer 1997; Gilmore, Lie Groups, Lie Algebras, and Some of Their Applications, John Wiley 1974; Edward Dunne's web site; Coquereaux and Jadczyk, Conformal Theories, Curved Phase Spaces Relativistic Wavelets and the Geometry of Complex Domains, Reviews in Mathematical Physics, Volume 2, No 1 (1990) 1-44, which can be downloaded from the web as a 1.98 MB pdf file.
...
...