Deriving the Standard Model plus Gravitation
from Simple Operations on Finite Sets
by Tony Smith
Table of Contents:
Chapter 1 - Introduction.
Chapter 2 - From Sets to Clifford Algebras.
Chapter 3 - Octonions and E8 lattices.
Chapter 4 - E8 spacetime and particles.
Column Spinors and Fermions.
Row Spinors and Vector Spacetime.
Dimensional Reduction
Spinors and Papapetrou Equations.
Bivector Gauge Bosons and Higgs Scalar.
Conformal Moebius Clifford Transformations
Clifford Algebras
Division Algebras
Weyl Groups and Root Vectors
gluon confinement
Casimir operators and questions of signature.
Complex Domains and Shilov Boundaries.
Other Multivectors.
Subtle Triality Supersymmetry.
Ultraviolet Finiteness and Renormalization.
Chapter 5 - HyperDiamond Lattices.
Chapter 6 - Spacetime and Internal Symmetry Space.
Chapter 7 - Feynman Checkerboards.
Chapter 8 - Charge = Amplitude to Emit Gauge Boson.
Chapter 9 - Mass = Amplitude to Change Direction.
Chapter 10 - Protons, Pions, and Physical Gravitons.
Appendix A - Errata for Earlier Papers.
References.
The 256-dimensional Clifford algebra DCl(0,8) has graded structure grade 0 1 2 3 4 5 6 7 8 dimension 1 8 28 56 70 56 28 8 1 *-grade 8 7 6 5 4 3 2 1 0 The Hodge star * map takes the 70-dimensional 4-vector space into itself. Therefore, the 70-dimensional 4-vector space splits into two 35-dimensional parts that are interchanged by the Hodge star * map. The grade-0 scalar of DCl(0,8) is 1-dimensional, representing the Higgs scalar field. The grade-1 vectors of DCl(0,8) are 8-dimensional, representing spacetime prior to dimensional reduction. The grade-2 bivectors of DCl(0,8) are 28-dimensional, representing a Spin(0,8) gauge group prior to dimensional reduction.
Spinor Fermion Particles and Antiparticles: 256-dimensional Cl(8) can be represented by a 16x16 real matrix algebra. The numbers refer to the grade in Cl(8) of the matrix entry. 0 2 2 2 2 2 2 2 7 5 5 5 5 5 5 5 4 4 2 2 2 2 2 2 5 7 5 5 5 5 5 5 4 4 4 2 2 2 2 2 5 5 7 5 5 5 5 5 4 4 4 4 2 2 2 2 5 5 5 7 5 5 5 5 4 4 4 4 4 2 2 2 5 5 5 5 7 5 5 5 4 4 4 4 4 4 2 2 5 5 5 5 5 7 5 5 4 4 4 4 4 4 4 2 5 5 5 5 5 5 7 5 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 7 * 1 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 3 1 3 3 3 3 3 3 6 4 4 4 4 4 4 4 3 3 1 3 3 3 3 3 6 6 4 4 4 4 4 4 3 3 3 1 3 3 3 3 6 6 6 4 4 4 4 4 3 3 3 3 1 3 3 3 6 6 6 6 4 4 4 4 3 3 3 3 3 1 3 3 6 6 6 6 6 4 4 4 3 3 3 3 3 3 1 3 6 6 6 6 6 6 4 4 3 3 3 3 3 3 3 1 6 6 6 6 6 6 6 8 Important Notation Notes: The two blocks of the form 0 2 2 2 2 2 2 2 4 4 2 2 2 2 2 2 4 4 4 2 2 2 2 2 4 4 4 4 2 2 2 2 4 4 4 4 4 2 2 2 4 4 4 4 4 4 2 2 4 4 4 4 4 4 4 2 4 4 4 4 4 4 4 4 are more symbolic than literal. They mean that: the 28 entries labelled 2 correspond to the antisymmetric part of an 8x8 matrix; the 35 entries labelled 4 correspond to the traceless symmetric part of an 8x8 matrix; and the 1 entry labelled 0 corresponds to the trace of an 8x8 matrix. A more literal, but more complicated, representation of the graded structure of those two blocks is: 0 2,4 2,4 2,4 2,4 2,4 2,4 2,4 2,4 4 2,4 2,4 2,4 2,4 2,4 2,4 2,4 2,4 4 2,4 2,4 2,4 2,4 2,4 2,4 2,4 2,4 4 2,4 2,4 2,4 2,4 2,4 2,4 2,4 2,4 4 2,4 2,4 2,4 2,4 2,4 2,4 2,4 2,4 4 2,4 2,4 2,4 2,4 2,4 2,4 2,4 2,4 4 2,4 2,4 2,4 2,4 2,4 2,4 2,4 2,4 4 However, in the more literal representation, the entries are not all independent. The more symbolic representation is a more accurate reflection of the number of independent entries of each grade. The two blocks of the form 1 3 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 3 1 can be taken more literally, as they mean that: the 8 entries labelled 1 correspond to the diagonal part of an 8x8 matrix; and the 56 entries labelled 3 correspond to the off-diagonal part of an 8x8 matrix. The conventions of the above Notation Notes are used from time to time in my papers and web pages. The even subalgebra of Cl(8) is 128-dimensional: 0 2 2 2 2 2 2 2 4 4 2 2 2 2 2 2 4 4 4 2 2 2 2 2 4 4 4 4 2 2 2 2 4 4 4 4 4 2 2 2 4 4 4 4 4 4 2 2 4 4 4 4 4 4 4 2 4 4 4 4 4 4 4 4 * 4 4 4 4 4 4 4 4 6 4 4 4 4 4 4 4 6 6 4 4 4 4 4 4 6 6 6 4 4 4 4 4 6 6 6 6 4 4 4 4 6 6 6 6 6 4 4 4 6 6 6 6 6 6 4 4 6 6 6 6 6 6 6 8 The entire 256-dimensional DCl(0,8) can be represented by 16x16 matrices. Each column or row of DCl(0,8) is a 16-dimensional minimal left or right ideal of DCl(0,8), and can be represented by two integral octonions. Each of the two integral octonions in a column minimal left ideal is a half-spinor, one +half-spinor and the other a mirror image -half-spinor. The basis elements for the column left-deal +half-spinor integral octonions correspond to first-generation fermion particles. Octonion Fermion Grade Structure Basis Element Particle of Column Vector 1 e-neutrino 0 2,4 2,4 2,4 2,4 2,4 2,4 2,4 i red up quark 2,4 4 2,4 2,4 2,4 2,4 2,4 2,4 j green up quark 2,4 2,4 4 2,4 2,4 2,4 2,4 2,4 k blue up quark 2,4 2,4 2,4 4 2,4 2,4 2,4 2,4 I red down quark 2,4 2,4 2,4 2,4 4 2,4 2,4 2,4 J green down quark 2,4 2,4 2,4 2,4 2,4 4 2,4 2,4 K blue down quark 2,4 2,4 2,4 2,4 2,4 2,4 4 2,4 E electron 2,4 2,4 2,4 2,4 2,4 2,4 2,4 4 Octonion Fermion Basis Element Particle 1 e-neutrino i red up quark j green up quark k blue up quark I red down quark J green down quark K blue down quark E electron The basis elements for the column left-deal -half-spinor integral octonions correspond to first-generation fermion antiparticles.
This is consistent with Sidharth's picture of Quark Fractional Charges based on T11, T22, and T33 components of the Stress-Energy Tensor Tij. The correspondence is more easily seen by representing the Octonion Basis Elements in terms of Triples of SU(2) = Spin(3) spinors, denoted by 1 and 0.
Octonion Triple of
Basis Element SU(2)=Spin(3) Spinors
1 0 x 0 x 0
i 1 x 1 x 0
j 1 x 0 x 1
k 0 x 1 x 1
I 0 x 0 x 1
J 0 x 1 x 0
K 1 x 0 x 0
E 1 x 1 x 1
The correspondence is related to the fact that the Spin(3) Clifford Algebra, Cl(3), can be deformed into the Octonion algebra.
Dimensional Reduction of Physical Spacetime produces 3 Generations of spinor fermion particles and antiparticles. The row minimal right ideal half-spinors correspond to the Clifford algebra gammas of spacetime transformations.
The entire 256-dimensional DCl(0,8) can be represented by 16x16 matrices. Each column or row of DCl(0,8) is a 16-dimensional minimal left or right ideal of DCl(0,8), and can be represented by two integral octonions. Each of the two integral octonions in a row minimal right ideal is a half-spinor, one +half-spinor and the other a mirror image -half-spinor. The 8 row minimal right ideal +half-spinors correspond to the 8-dim spacetime position. The 8 row minimal right ideal -half-spinors correspond to the momenta dual to 8-dim spacetime postion. The 8 basis elements for the +half-spinor integral octonions and for the -half-spinor integral octonions each correspond, by triality, to the 8 basis elements of the Cl(8) vector space, and therefore to the 8-dimensional spacetime gamma matrices: Octonion Gamma Grade Structure Basis Element Matrix of Row Vector 1 Gamma1 0 2,4 2,4 2,4 2,4 2,4 2,4 2,4 i Gamma2 2,4 4 2,4 2,4 2,4 2,4 2,4 2,4 j Gamma3 2,4 2,4 4 2,4 2,4 2,4 2,4 2,4 k Gamma4 2,4 2,4 2,4 4 2,4 2,4 2,4 2,4 I Gamma5 2,4 2,4 2,4 2,4 4 2,4 2,4 2,4 J Gamma6 2,4 2,4 2,4 2,4 2,4 4 2,4 2,4 K Gamma7 2,4 2,4 2,4 2,4 2,4 2,4 4 2,4 E Gamma8 2,4 2,4 2,4 2,4 2,4 2,4 2,4 4
After Dimensional Reduction to 4-dimensional spacetime,
the 8 Gammas of the 8-dimensional vector space of Cl(8)
are replaced by 4 Gammas of the 4-dimensional spacetime,
with the 1 4 6 4 1 graded structure
0 2 3 3
2 2 3 3
1 1 2 2
1 1 2 4
with the even subalgebra graded structure being
0 2
2 2
2 2
2 4
so that the 4-dimensional physical spacetime Gammas
have Quaternion structure and graded structure
Quaternion Gamma Grade Structure
Basis Element Matrix of Row Vector
1 Gamma1 0 2
i Gamma2 2 2
j Gamma3 2 2
k Gamma4 2 4
Therefore, physical 4-dimensional spinors are represented
as bivectors (or bivector plus scalar or pseudoscalar).
Since bivectors generate rotations (or boosts),
physical spinors transform under transformations of spacetime
like spinning (rotating) spheres.
Since gravity can be represented in 4-dimensional spacetime
by geometric transformations of spacetime,
the interaction between spinors and gravity can
be represented by curvature in a Clifford Manifold,
as done by William Pezzaglia in gr-qc/9710027 in his
derivation of the Papapetrou Equations.
Pezzaglia's picture may be consistent with
the picture of G. Sardanashvily and of the D4-D5-E6-E7 model
with respect to Gravity and the Higgs Mechanism.
For a more conventional derivation of the Papapetrou Equations,
see, for example, Geometric Quantization, by N. Woodhouse,
second edition Clarendon Press 1992, pages 127-129.
To me, the Clifford method of William Pezzaglia semms
clearer than the more conventional derivation,
particularly with respect to fundamental fermions
and massless (at tree level) neutrinos.
The Papapetrou Equations are important because
they show that gravity acts on spinor particles,
even if they are massless.
Torsion comes from spin, and both are related to physics models using Conformal Weyl curvature.
Click Here to see more about Torsion Physics.
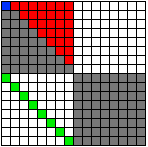
You can use Clifford Algebras to see how Dimensional Reduction affects the bivector Gauge Bosons and the Higgs scalar. The process in the (1,7) signature of the D4-D5-E6-E7-E8 VoDou Physics model is described HERE. From a Euclidean point of view, consider DCl(0,8):
Here: the 1-dimensional scalar 0-grade subspace is blue, and the 28-dimensional bivector 2-grade subspace is red. The 8-dimensional vector 1-grade subspace, shown in green, breaks down into 4-dimensional Physical Spacetime plus 4-dimensional Internal Symmetry Space. To see how a Euclidean path works, first go from DCl(0,8) to its even subalgebra DCle(0,8) which is the Clifford algebra DCl(0,7):
+
then go to its even subalgebra DCle(0,7) which is the Clifford algebra DCl(0,6):
then go to its even subalgebra DCle(0,6):
which is the Clifford algebra DCl(0,5):
+
The two components of DCl(0,5) can be regarded
as Real and Imaginary parts.
The 4x4 = 16 components of the Real part of DCl(0,5) are:
1-dimensional U(1) propagator phase (light blue); and
15-dimensional Conformal group that gauges to produce Gravity
from the MacDowell-Mansouri mechanism and 10 Poincare group
generators (red), with gravitons that see their Symmetry Space
of Spacetime according to their group symmetry,
and 5 Conformal degrees of freedom (brown) that,
when gauge-fixed, combine with the scalar to
produce the Higgs mechanism;
The 1 + 12 + 3 components of the Imaginary part of DCl(0,5) are:
1-dimensional Higgs scalar, that combines with the gauge-fixed
Conformal degrees of freedom to
produce the Higgs mechanism;
12 Standard Model gauge bosons, 3 for weak SU(2) (red),
9 for 8 SU(3) gluons, and 1 U(1) photon (yellow),
that see Internal Symmetry Space according
to their group symmetry;
and
3 components that are 4-vectors (gray), not bivectors,
and do not contribute to
the physics of gauge bosons and the scalar.
The Standard Model U(1)xSU(2)xSU(3) Lie algebra structure acts on the 8-dimensional generalized half-Spinor space of Cl(6) through:
If each of U(1), SU(2), and SU(3) are considered to act respectively on C, Q, and O, then the Standard Model Lie algebra U(1)xSU(2)xSU(3) can be considered as acting on the 2x4x8=64-dimensional tensor product space T = C x Q x O (which is a non-alternative algebra).
Using T = C x Q x O to describe the Standard Model is the idea of Geoffrey Dixon. To see how his approach works, let the basis for the Complex numbers be {1,i}, the basis for the Quaternions be {1,i,j,k}, and the basis for the Octonions be {1,i,j,k,E,I,J,K}, and denote by q an imaginary unit quaternion, and then decompose the Identity of T by using
to form 4 orthogonal associative primitive idempotent projection operators
whose symmetries are
SUq(2) is an SU(2) symmetry due to the variability of the imaginary unit Quaternion q over the entire S3 = SU(2) of imaginary unit Quaternions. If q were fixed (with respect to i) then the 2 SU(2) symmetries would be synchronized, and the resulting symmetries would be
Ui(1), Uq(1), and UE(1) are U(1) symmetries due to the variability of each imaginary unit Quaternions over the S1 spanned by it in the parallelizable S3, and to the variability of the imaginary unit Octonion over the S1 spanned by it in the parallelizable S7. If the imaginary unit Quaternions and Octonion were fixed, then the 4 U(1) symmetries would be synchronized, and the resulting symmetries would be
which is the Standard Model Lie algebra U(1)xSU(2)xSU(3).
In his book, Geoffrey Dixon noted that his approach, like mine, produced the Lie algebra
prior to synchronization of the U(1)'s and the SU(2)'s.
Note - My terms, generalized Spinor and generalized half-Spinor space of Cl(6), are not standard mathematical terms but are used here because they seem to me to be useful.
The Gauge Boson dimensional reduction process of the D4-D5-E6-E7 physics model can also be described from a geometric Weyl Group - Root Vector Space point of view,
In the above discussion I have indicated that I think that Spin(2,4) (sometimes I have written Spin(4,2), but sign conventions vary and I think that --++++ is the correct signature) is the proper global structure for the conformal group of -+++ (1,3)-dim physical spacetime. I often leave out considerations of signature in discussing the breakdown of Spin(8), because:
From the Clifford algebra point of view:
The number and order of the Casimir invariant operators do not depend on the signature, so here are some of them:
The Casimirs are invariant under the Weyl group which is the reflection group related to the root vectors that I use in the decomposition 28 = 15 + 1 + 8 + 3 + 1. I have not worked out details, but it seems likely that the Weyl group breakdown will tell you how the Casimirs are related and to be interpreted. The order of the Weyl group is the product of the orders of the Casimirs.
According to Group Structure of Gauge Theories by O'Raifeartaigh (Cambridge 1986), the Casimir of order 2 is related to the Cartan metric g^ab by
and, if F is the fundamental representation of G, then C2(F) = dim(G) / dim(F). The index of a representation j is given by
The index is important in renormalization of non-abelian gauge theories.
As Heinrich Saller has indicated, mass/energy and spin are candidates for physical interpretations of Casimirs, and I think that other candidates are isospin - related to SU(2) gauge bosons carrying electric charge and color charge. How to study the Casimirs?
Start with Spin(4,4). It is rank 4, and has 4 Casimirs.
Now combine Spin(2,4) = SU(2,2) with U(1) to get U(2,2).
Now look at the symmetric space (maybe I am getting mixed up about some signatures here, but I will go on anyway) Spin(4,4)/U(2,2), or Spin(0,8)/U(2,2). It is a rank-2 12-dimensional symmetric space of type D III. As a rank-2 space, it has 2 Casimirs, which should be related to 4-dim internal symmetry space and the 12-dim Standard Model.
That leaves 2 other Casimirs from Spin(4,4), or Spin(0,8), to be used with respect to the 4-dim physical spacetime.
In calculations, it is sometimes convenient to use the volumes of compact manifolds that represent spacetime, internal symmetry space, and fermion representation space. The compact manifold that represents 8-dim spacetime is RP1 x S7, the Shilov boundary of the bounded complex homogeneous domain that corresponds to Spin(10) / (Spin(8)xU(1)). It represents the invariant measure on the noncompact space Spin(1,9) / (Spin(8)xU(1)).
Note that S1/Z2 can be described as an orbifold.
The compact manifold that represents 4-dim spacetime is RP1 x S3, the Shilov boundary of the bounded complex homogeneous domain that corresponds to Spin(6) / (Spin(4)xU(1)). It represents the invariant measure on the noncompact space Spin(2,4) / (Spin(1,3)xU(1)). The compact manifold that represents 4-dim internal symmetry space is RP1 x S3, the Shilov boundary of the bounded complex homogeneous domain that corresponds to Spin(6) / (Spin(4)xU(1)). It represents the invariant measure on the noncompact space Spin(2,4) / (Spin(1,3)xU(1)). The compact manifold that represents the 8-dim fermion representation space is RP1 x S7, the Shilov boundary of the bounded complex homogeneous domain that corresponds to Spin(10) / (Spin(8)xU(1)). It represents the invariant measure on the noncompact space Spin(1,9) / (Spin(8)xU(1)). The manifolds RP1 x S3 and RP1 x S7 are homeomorphic to S1 x S3 and S1 x S7, which are untwisted trivial sphere bundles over S1. The corresponding twisted sphere bundles are the generalized Klein bottles Klein(1,3) Bottle and Klein(1,7) Bottle.
As to the remaining Multivectors of DCl(0,8):
35 of the 70 4-vectors in the 4-grade subspace are represented in gray. They are the symmetric parts of the upper left 8x8 diagonal subspace, remaining after taking out the 1-dimensional scalar 0-vector Higgs scalar. The 1-dimensional scalar 0-vector representing the Higgs scalar can be thought of as the trace of the full symmetric 1+35=36-dimensional space of symmetric 8x8 real matrices. The 35 4-vectors are the traceless symmetric 8x8 matrices. They are related to the coassociative 4-form that is fixed in the dimensional reduction process to determine the internal symmetry space. At our low energy levels, below the Planck-scale at which dimensional reduction occurs in the D4-D5-E6-E7 model, the 35 4-vectors do not play a dynamical role that we can test experimentally here and now. The 56-dimensional trivector 3-grade subspace is represented in white. In the full 8-dimensional theory, the 56 trivectors are related to the structure of 3+1=4-dimensional subspaces of 1+7=8-dimensional spacetime that are connected with the E8 HyperDiamond lattice links that are (normalized) sums of 4 of the basis octonions. To reduce the dimension of spacetime to 1+3=4 dimensions, an associative 3-form is used. This effectively fixes a particular trivector, so the 56 trivectors do not play a dynamical role in the 4-dimensional phase of the D4-D5-E6 model. The other 35 56 28 8 1 are (by Hodge * duality) located symmetrically on the opposite side of the 16x16 matrix. By Hodge duality, they can be viewed as the structures of the D4-D5-E6-E7 model that act on the antiparticle half-spinor fermions, while the 1 8 28 56 35 can be viewed as acting on the particle half-spinor fermions.
Here is the Dynkin diagram for Spin(8). Each vertex represents a representation of Spin(8), with the center vertex (Spin(8)) corresponding to the 28-dimensional adjoint representation that I identified with gauge bosons.
The three representations for spacetime (blue dot), fermion particles (red dot), and fermion antiparticles (green dot) are EACH 8-dimensional with Octonionic structure. They are ALL isomorphic by the Spin(8) Triality Automorphism, which can be represented by rotating or interchanging the 3 arms of the Dynkin diagram of Spin(8). The Triality isomorphism between spacetime and fermion particles and fermion antiparticles constitutes a SUBTLE SUPERSYMMETRY between fermions and spacetime.
may be seen by considering, prior to dimensional reduction, the generalized supersymmetry relationship between the 28 gauge bosons and the 8 (first-generation) fermion particles and antiparticles. In the 8-dimensional spacetime, the dimension of each of the 28 gauge bosons in the Lagrangian is 1, and the dimension of each of the 8 fermion particles is 7/2, so that the total dimension 28x1 = 28 of the gauge bosons is equal to the total dimension 8x(7/2) = 28 of the fermion particles. After dimensional reduction of spacetime to 4 dimensions, the 8 fermions get a 3-generation structure and the 28 gauge bosons are decomposed to produce the Standard Model of U(1) electromagnetism, SU(2) weak force, and SU(3) color force, plus a Spin(5) = Sp(2) gauge field that can produce gravity by the MacDowell-Mansouri mechanism.
Note that both Gravity and the Standard Model forces are required for the cancellations that produce the ultraviolet finiteness that is useful in the Sakharov Zero Point Fluctuation model of gravity.
The Conformal Structure of the D4-D5-E6-E7-E8 VoDou Physics model includes the symmetry of Conformal Group Dilations, which transform the scale of length/energy/mass, which gives the scale transformation properties needed for Renormalization.
From Sets to Quarks: Table of Contents: Chapter 1 - Introduction. Chapter 2 - From Sets to Clifford Algebras. Chapter 3 - Octonions and E8 lattices. Chapter 4 - E8 spacetime and particles. Chapter 5 - HyperDiamond Lattices. Chapter 6 - Spacetime and Internal Symmetry Space. Chapter 7 - Feynman Checkerboards. Chapter 8 - Charge = Amplitude to Emit Gauge Boson. Chapter 9 - Mass = Amplitude to Change Direction. Chapter 10 - Protons, Pions, and Physical Gravitons. Appendix A - Errata for Earlier Papers. References.
......