The D4-D5-E6-E7 model coset spaces E7 / (E6 x U(1)) and E6 / (D5 x U(1)) and D5 / (D4 x U(1)) are Conformal Spaces. You can continue the chain to D4 / (D3 x U(1)) where D3 is the 15-dimensional Conformal Group whose compact version is Spin(6), and to D3 / (D2 x U(1)) where D2 is the 6-dimensional Lorentz Group whose compact version is Spin(4).
Note that D3 inherits a non-linear version of triality from the full triality of D4.
Electromagnetism, Gravity, and the ZPF all have in common the symmetry of the 15-dimensional D3 Conformal Group whose compact version is Spin(6), as can be seen by the following structures with D3 Conformal Group symmetry:
Further, the 12-dimensional Standard Model Lie Algebra U(1)xSU(2)xSU(3) may be related to the D3 Conformal Group Lie Algebra in the same way that the 12-dimensional Schrodinger Lie Algebra is related to the D3 Conformal Group Lie Algebra.
The physical 4-dimensional SpaceTime of the D4-D5-E6-E7-E8 VoDou Physics model is a 4-dimensional HyperDiamond lattice SpaceTime that is continuously approximated globally by RP1 x S3 and locally by Minkowski SpaceTime, with Gravity coming from the 15-dimensional Conformal Group Spin(2,4) by the MacDowell-Mansouri mechanism. The curved SpaceTime of General Relativity is not considered fundamental, but is produced by by starting with a linear spin-2 field theory in flat spacetime, and then adding higher-order terms to get Einstein-Hilbert gravity. The observed curved SpaceTime is therefore based on an unobservable flat Minkowski SpaceTime. (See Feynman, Lectures on Gravitation, Caltech 1971 and Addison-Wesley 1995, and see Deser, Gen. Rel. Grav. 1 (1970) 9-18 as described in Misner, Thorne, and Wheeler, Gravitation, Freeman 1973, pp. 424-425.)
If you were to start, not with locally Minkowski SpaceTime, but with the curved SpaceTime of General Relativity, then you would see that the Conformal transformations of Minkowski SpaceTime by the 15-dimensional Conformal Group Spin(2,4) corresponds to the Conformal transfomations of the curved SpaceTime by the infinite-dimensional Conformal subgroup of the group Diff(M4) of General Relativistic coordinate transformations of the 4-dimensional SpaceTime M4 of General Relativity, which Conformal subgroup is defined as those General Relativistic coordinate transformations that preserve conformal structure and which infinite-dimensional Conformal subgroup can be called the Weyl Conformal Group. (See Ward and Wells, Twistor Geometry and Field Theory, Cambridge 1991, p. 261.)
The Presentations of the 15 Infinitesimal Causal Symmetries of Segal's Conformal SpaceTime are given in the following Table 1. from Proc. Nat. Acad. Sci. USA 78 (1981) 5261-5265, by I. E. Segal, H. F. Jakobsen, B. Oersted, S. M. Paneitz, and B. Speh:

In his book Mathematical Cosmology and Extragalactic Astronomy (Academic Press 1976) (pages 72-75, 88-91), Segal says:
"... The suitably scaled 15 linearly independent generators Lij of symmetries of unispace [Segal's term for the Conformal RP1 x S3 SpaceTime used in the D4-D5-E6-E7 model - from here on on this page I will call it Conformal SpaceTime] ... differ from the 11 generators of the group of global conformal transformations in Minkowski space
[as R becomes infinite, where R is the radius of curvature of Conformal SpaceTime] ...
... The angular momenta Lij ... [ i,j = 1,2; 2,3; 3,1 ] ... have ... the same expression both in Minkowski space and in [Conformal SpaceTime] ... The same is true of the boosts ... -iL0,j ... ( j = 1,2,3 ) ... and the infinitesimal scale transformation [ L-1,4 ] ...
... The scale generator - L-1,4 ... determines a ... scalar field. This ... is most naturally interpreted from a gravitational standpoint ...
... two ordered sets, each containing four of the Lij, converge on the same ... fields in Minkowski space ... in particular, R^(-1) L-1,j and R^(-1) Lj,4 [ for j = 0,1,2,3 ] both ... agree ... [as R becomes infinite] with the [corresponding Minkowski] conventional energy-momentum component. ... The differences
thus are ... representable by a ... vector field, which physically would appear most naturally as potentially related to gravitational phenomena ... ".
First,
Then,
GraviPhotons look like:
Virtual Covariant Conventional U(1) Photons, in that they have 4 Components, including Longitudina/Scalar Components; andVector Gravitons that can interact with the Imaginary Part of Complex Spacetime.
In the D4-D5-E6-E7 physics model, 4-dimensional Physical Spacetime is the Shilov Boundary of an 8-real-dimensional Bounded Complex Homogeneous Domain corresponding to the Hermitian Symmetric Space Spin(2,4) / Spin(4) x Spin(2) = SU(2,2) / S(U(2)xU(2)), which symmetric space is a 15-6-1 = 8-real-dimensional space with Complex structure, or a 4-Complex-dimensional space.
The 4-real dimensional Shilov Boundary is RP1 x S3, which is topologically equivalent to S1 x S3, where S1 is time and S3 is space. If you suppress one space dimension, Spacetime looks like this

where the gold is the interior 2-disk of the blue 1-sphere S of Time and the red is the interior 4-ball of the green 3-sphere S3 of Space.
If the S1 x S3 Physical Spacetime is regarded as the 4-dimensional Real Part of 8-real-dimensional Complex Spacetime, then the Imaginary Part of 8-real-dimensional Complex Spacetime is found in the Interior. The 4 real dimensions of the Imaginary Part are generated by:
Of the 15 Conformal gravitons,
the 1 scale generator, or dilation, does not change the geometric relationship between the Shilov Boundary Real Part and the Interior Imaginary Part;
but
the 4 GraviPhotons can go from the Shilov Boundary Real Part into the Interior Imaginary Part.
By the Harmonic structure of the D4-D5-E6-E7 physics model:
any Continuous Function on the Shilov Boundary S1 x S3 Real Part can be extended to a Harmonic Function throughout the entire 8-real-dimensional Complex Spacetime;the Harmonic Functions form a basis in terms of which you can express any Analytic Function in the entire 8-real-dimensional Complex Spacetime; and
if you know an Analytic Function in any neighborhood, no matter how small, you can use Analytic Continuation to know that Analytic Function everywhere in the entire 8-real-dimensional Complex Spacetime.
A couple of notes: you can probably get the same results by looking at the 8-real-dimensional SpaceTime as a 2-Quaternionic-dimensional space (with Fueter's Quaternioinic analyticity and Quaternionic Cauchy-Riemann equations as described, for example, in On the Role of Division, Jordan and Related Algebras in Particle Physics, by Feza Gursey and Chia-Hsiung Tze (World 1996)) or by looking at the 8-real-dimensional SpaceTime as a 1-Octonionic-dimensional space; and, according to YGGDRASIL (journal of paraphysics whose name is "... the "world tree" in Norse mythology. It is also known as the "tree of knowledge," the "tree of the universe" and the "the tree of fate." ..."), the idea of looking at the imaginary part of an 8-real-dimensional SpaceTime was used by Elizabeth Rauscher in 1977 and Puthoff, Targ and Edwin May in 1979.
As Vector Gravitons they can (considered as gauge bosons) be attractive or repulsive and can (considered as contributors to the general relativistic shape of SpaceTime) transform SpaceTime in their neighborhood.
The Dilation sets the scale of the Higgs VeV at 250 GeV so that general deformations of SpaceTime can take place only above that energy level, while GraviPhotonSpecial Conformal (Hopf flow) transformations are useful in Conformal deformations of SpaceTime.
Incompressibility of the Aether below 250 GeV is only with respect to the 6-dim vector space of the Conformal Group Spin(2,4), so that below 250 GeV you can see Conformal phenomena that appear to show compressibility from the point of view of 3-dim space or 4-dim Minkowski spacetime. Such conformal phenomena include the Fock superluminal solutions of Maxwell's equations that are described by R. M. Kiehn.
The 4 GraviPhoton Special Conformal transformations are like the Moebius linear fractional transformations, that do deform Minkowski spacetime but take hyperboloids into hyperboloids and are the symmetries of superluminal solutions of the Maxwell equations. They are incompressible/linear from the point of view of a 6-dimensional SpaceTime, with 4 spatial dimensions and 2 time dimensions, because the conformal group over Minkowski spacetime is just SU(2,2) = Spin(2,4), the covering group of SO(2,4), and therefore the Lie algebra generators look like those of rotations in a 6-dim vector space of signature (2,4). This is the 4-dim space with 2-dim time suggested by Robert Neil Boyd, in which things look linear (even though from our conventional 3-dim spatial or 4-dim Minkowski point of view they might appear, due to our limited conventional perspective, to be nonlinear). If you regard Physical SpaceTime as the 6-dimensional vector space of Spin(2,4), and Internal Symmetry Space as 4-dimensional CP2, then the total space is 6+4=10-dimensional. With respect to tthe D4-D5-E6-E7 model, that 10-dim space corresponds:
to the 10-dim vector space of the D5 Lie Algebra Spin(2,8); andto the 10-dim element of the decomposition of the 27-dim representation of the E6 Lie Algebra into 10 + 16 + 1 under its D5 subalgebra (see, for example, Lie Algebras in Particle Physics, 2nd edition, by Howard Georgi, Perseus Books (1999), page 308).
The corresponding Complex Linear Fractional Moebius Transformations can be used to visualize the usefulness of GraviPhoton SpaceTime Shape-Changing. For example,the Elliptic Complex Linear Fractional Moebius Transformations can be used to make a Complex version of a type of Alcubierre Warp Drive that moves through space by the Alcubierre mechanism (Classic and Quantum Gravity 11 (1994) L73) in which you "... create a local distortion of spacetime that will produce an expansion behind the spaceship, and an opposite contraction ahead of it. In this way, the spaceship will be pushed away from the earth and pulled towards a distant star by spacetime itself. ...". Since the spacetime around the spaceship is not distorted, the spaceship and its contents feel no G-forces from acceleration.
(Note: My reference to Alcubierre's warp drive is intended to refer only to the general idea of contracting spacetime ahead of a ship and expanding spacetime behind a ship. I do NOT say that what I propose uses the same physics mechanism by which Alcubierre actually proposes to accomplish this. In fact, my proposal is NOT equivalent to the mechanism used by Alcubierre. Among the differences, I do not have to build a bubble around the spaceship, while Alcubierre does have to do that.)
In the Elliptic Conformal Moebius Map shown above, a Ship around the two focal points on the Spatial Line would contract SpaceTime above it and pull it through the Ship/Points, while pushing away expanding SpaceTime to the bottom.
Consider the 2-dimensional Ship as being built around the two focal points.
Then consider the 2-dimensional Ship as being a 2-dimensional cross section of a 2-dim Torus in 4-dimensions (torus image from 3D-Filmstrip by Richard S. Palais):
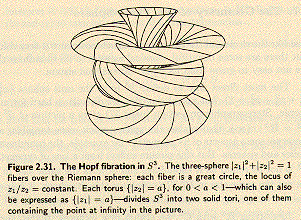
Then consider the 2-dim Torus as part of a Hopf Fibration of a 3-sphere S3 in 4-dimensions.
The Hopf Fibration is described by William Thurston in his book Three-Dimensional Geometry and Topology, volume 1, Princeton University Press 1997, pages 103-108, where he says:
"... Identifying R4 with C2 ... If the coordinates in C2 are z1 and z2, the equation of a unit sphere becomes | z1^2 + z2^2 | = 1. Each complex line ... in C2 intersects S3 in a great circle called a Hopf circle. Since exactly ond Hopf circle psses through each point of S3, the family of Hopf circles fills up S3, and the circles are in one-to-one correspondence with the complex lines of C2, that is, with the Riemann sphere CP1 ... Informally, the three-sphere is a two-sphere's worth of circles. Formally, we get a fiber bundle p : S3 -> S2, with fiber S1. ... We call this structure the Hopf fibration ... Figure 2.31 shows what the Hopf fibration looks like under stereographic projection. ... the vertical axis is the intersection of S3 with the complex line z1 = 0, and the horizontal circle is the intersectioin with z2 = 0. The locus { | z2 | < a }, for any 0 < a < 1, is a solid torus neighborhood of the z2 = 0 circle. Its boundary { | z2 | = a }, a torus of revolution, is filled up by Hopf circles, each winding once around the z1-circle and once around the z2-circle. ... any torus of revolution has cirves winding around in both directions that are geometric circles ... [called] ... Villarceau circles. ...... the maps gt : S3 -> S3 given by multiplication by exp( i t ), for t in R, are isometries and ... leave the Hopf fibration invartiant. Thus S3 has isometries that do't have an axis: the motion near any point is like the motion near any other point. This is one way in which S3 seems rounder than S2. The one-parameter family { gt } is called the Hopf flow. ...
... The descriptions of S3 via quaternions and via complex numbers can be combined. If we look at [the quaternions] as a complex vector space, multiplication on the left by the quaternion i is the same as multiplication by the complex number i, so the vector field Xi(p) = i p , for p in S3, induces the Hopf flow on S3. ... because i plays no special role among the quaternions ... any pure quaternion of unit norm can be used in lieu of i ... Thus there are many Hopf flows and many Hopf foliations on S3. In particular, we can take three mutually orthogonal vector fields Xi, Xj, and Xk to get three mutually orthogonal families of Hopf circles. ...
... If g in S3 is not +/- 1, the transformation x -> g x fits into the unique Hopf flow generated by the Hopf field x -> p x , where p is the unit quaternion in the direction of the g purely imaginary component of g . Similarly when h in S3 is not +/- 1 , the transformation x -> x h fits into a unique Hopf flow, generated by a vector field x -> x p . The two kinds of Hopf flows are distinguished as left-handed or right-handed: the circles near a given circle wind around it in a left-handed sense or in a right-handed sense ... any right-handed Hopf flow commutes with any left-handed Hopf flow. ...". In a given Hopf Fibration, any two Hopf circles are linked.
In terms of the Space S3, the GraviPhoton Moebius Alcubierre Warp Drive looks like a vortex in which the Destination Space is pulled along the Hopf Flow Circles in toward the ship and, after the ship passes through it, is expelled behind the ship.
Physically, the 4 covariant polarizations (t,x,y,z) of a GraviPhoton moving in the z-direction correspond to:
The structure is that of a Penrose Twistor, as described in the book Spinors and Spacetime, volume 2, by Penrose and Rindler (Cambridge 1986), pages 61-62: "... These curves are ... circles ... They twist around one another (hence the term twistor!) in such a way that every pair of circles is linked ...
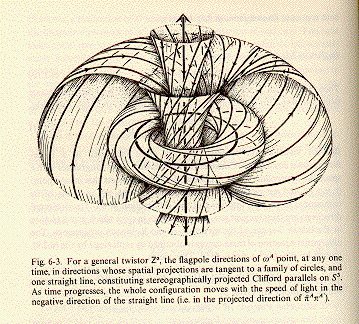
... They lie on the set of coaxial tori ... [that] ... are the rotations about the z-axis of a system of coaxial circles in the (x,z)-plane. From the point of view of the compactified space-time ... we should regard the hyperplane t = tau as being compactified (conformally) by a point at infinity. It then becomes topologically a three-dimensional sphere S3 (of which the hyperplane t = tau may be regarded as the stereographic projection). The vector field on S3 is everywhere nonsingular and nowhere vanishing. The circles constitute what is known as a Hopf fibring of S3. With a suitable scaling they become Clifford parallels on S3. ... all the circles in the hyperplane thread through the particular (smallest) circle ... the radius of this smallest circle ... is given, generally, ... by the spin divided by the energy ...".
A sequence of Hopf tori, each made up of Hopf-Clifford circles, is shown in a .mpg movie on a UBC web page. Here are three of the Hopf tori from that movie:



Why Electrons? Because an Electron is a spin 1/2 particle, so that it is not only a localized particle, but that it is Entangled with and Connected to the Global Universe in which it is located. Spin 1/2 particles orientation-entangled with their environment are Fermions and their intrinsic orientation-entanglement can be mathematically described by saying that Fermions are Quaternionic.
To see how orientation-entanglement works, look at this picture from Gravitation, by Misner, Thorne, and Wheeler (Freeman 1972):

The orientation of the ball is related to the surrounding sphere by the tangle of the strings connecting them. As Louis H. Kauffman says in his book Knots and Physics (World Scientific Publishing Co. 1991), a spin 1/2 particle is like a ball attached to its surroundings by string.
Is such a GraviPhoton connection between locat particles and the Global Universe a reasonable thing to see in our physical world?Another example is the graviton-based Mach's Principle connection between local things and the Global Universe, illustrated in Introduction to Cosmology, by J. V. Narlikar (2nd ed Cambridge 1993) by the curvature of the surface of water in a bucket that is spinning with respcct to the Global Universe:
In their book Gravitation (Freeman 1973), Misner, Thorne, and Wheeler say: "... Einstein's theory ... identifies gravitation as the mechanism by which matter there influences inertia here ...".

Then consider the 2-dimensional Ship as being a 2-dimensional cross section of a 2-dim Torus in 4-dimensions (torus image from 3D-Filmstrip by Richard S. Palais):

Then consider the 2-dim Torus as part of a Hopf Fibration of a 3-sphere S3 in 4-dimensions.
Then consider Electons, all in the same coherent Entanglement Connection phase, flowing coherently along Clifford-Hopf Circles (Clifford-Hopf torus (angle) images from 3D-Filmstrip by Richard S. Palais)
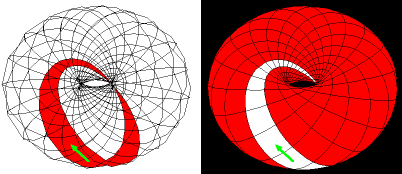
as shown by the green arrow on the red or white Clifford-Hopf Circle and thus coherently dragging the Rest of the Global Universe from above, into the central hole of the 2-Torus, and then out the bottom in a higher-dimensional version of the Elliptical Complex Conformal 2-dimensional flow.
By symmetry, every Clifford-Hopf Circle Flow (red or white) has a corresponding Opposite Flow (blue) (Clifford-Hopf torus (overhead) images from 3D-Filmstrip by Richard S. Palais)
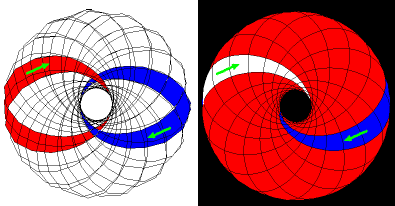
and, like all Clifford-Hopf Circles, they are linked with each other.
Effectively, the Electrons produce GraviPhotons that produce the 4-dimensional Conformal Flow. In terms of the Penrose and Rindler image,
Such Star-Gate Ring Ships might be regarded as a type of worm-hole, whose stability might be interpretable in terms of ghosts. and whose engineering might involve Rodin Coil ring structures.
How could a 2-Torus Ring Ship be engineered? Perhaps by using a fermionic version a Bose-Einstein Condensate. This could be related to a suggestion of Ivanenko and Vladimirov: Paul Hill (in Unconventional Flying Objects, Hampton Roads 1995) quotes D. D. Ivanenko and Yu. S. Vladimirov (in Matter and Physical Fields - Part One of The Earth in the Universe, translated 1968 in U.S. Department of Commerce Clearinghouse) as saying "... it may be possible for electron-positron pairs to be transformed not only into photons, but also into gravitons".
Instead of Frame-Dragging by Einstein Gravity, you have Entanglement Connection Dragging by flow of Spin 1/2 Electron Spinors, which is effectively Dragging by Torsion in Einstein-Cartan Gravity.
The GraviPhoton force strength factor is different from the gravitational G of the gravitational force equation F = G mM / r^2,
and is also different from force strength factor of the electric force equation between two unit electric charges F = e^2 / r^2 , where e is the electric charge, or amplitude for a single electron to emit or absorb a photon, and e^2 is the electromagnetic fine structure constant 1 / 137.03608.
In the Far Field region of gravity, the modifications for the GraviPhoton force are as follows:
Unlike gravitation, and like electromagnetism, the GraviPhoton force will cancel itself out in matter that is randomly oriented. The rotating astrophysical bodies that give evidence (described by Wesson) for the GraviPhoton force are rotating in a coordinated way such that the cancellation does not occur.
In the Near Field Induction/Static Region of Strong Gravity, the GraviPhoton force has the same strength as the other components of Gravity, which is the maximal value 1.
From the point of view of a neutral Kerr-Newman Black Hole, with coincident outer and inner event horizons, with irreducible mass M, angular momentum J, and charge Q:
Q^2 + (J/M)^2 = M^2
Dividing through by M^2, you get J^2/M^4 = (J/M^2)^2 = 1 - (Q/M)^2 Setting Q/M = x you get
(assuming that p_astro(Wesson) = (G/C) (1/alpha), with natural units G = c = 1 so that p_astro(Wesson) = 1 / alpha )
J = sqrt(1 - x^2) M^2 = p_astro(Wesson) M^2 = 137 M^2 so that 1 - x^2 = 137^2 and
Q/M = x = sqrt(-137^2) = 137 i = 137 exp(pi/2)
and sqrt(x) = 11.7 exp(pi/4). Since amplitudes are inherently complex, there is no problem with them being imaginary as well as negative or positive. Since x = Q/M, and sqrt(x) = sqrt( Q/M ), you get the magnitude
|sqrt(M)/sqrt(q)| = |sqrt( M/Q )| = 1/11.7 = 0.0855
Richard Feynman says in his book QED (Princeton 1988):
"... e - the amplitude for a real electron to emit or absorb a real photon.
It is a simple number that has been experimentally determined
to be close to -0.0854...
the inverse of its square: about 137.03... has been a mystery ...
all good theoretical physicists put this number up on their wall ...".
To see the physical meaning of the ratios Q/M and sqrt(M)/sqrt(q),
consider:
M^2 corresponds to area and
to number of classical q-bits of mass information,
represented by real numbers.
M, irreducible mass of black hole,
corresponds to length (square root of area) and
to number of quantum q-bits of mass information,
represented by complex numbers with complex phase.
sqrt(M) corresponds to spinor (square root of 4-vector) and
carries orientation/entanglement with 4-dim spacetime
represented by quaternions.
Q^2 corresponds to number of classical q-bits of charge information,
represented by real numbers.
Q, charge of black hole,
corresponds to number of quantum q-bits of charge information,
represented by complex numbers with complex phase.
sqrt(Q) corresponds to square root of charge,
which might be called a charge-spinor,
represented by quaternions.
The ratio sqrt(M) / sqrt(Q) = 0.0855
corresponds to the amplitude for a charge-spinor
to emit or absorb
a GraviPhoton whose quaternionic property
of orientation/entanglement with 4-dim spacetime
can alter 4-dim spacetime and its electromagnetic fields.
In randomly oriented situations, the GraviPhoton effects cancel out
and are not ordinarily observed.
In coherent situations (such as macroscopic rotating bodies)
the GraviPhoton alterations
of 4-dim spacetime and its electromagnetic fields
might be observed.
The ratio Q / M = 137 corresponds to
the fact that the charge Q of a Kerr-Newman black hole
carries more quantum information than its irreducible mass M
by a factor of about 137.
Tony Smith's Home Page ......