
M. Botta Cantcheff, in gr-qc/0010080, says: "... MacDowell and Mansouri proposed a gauge theory of gravity based on the group SO(3,2) ... we focus our attention on the equations of motion ... of a Y-M's [Yang-Mills's] theory ... the real difference between GR [General Relativity with cosmological constant] and an YM-theory ... is ... a single [YM] constraint which has an extremely simple interpretation: the torsion-free condition. ... Torsion appears in a natural way in modern formulations of the gravitational theories [ I. L. Shapiro, "Physical Aspects of the Space-Time Torsion", hep-th/0103093 ] ... by relaxing the constraint, we are naturally led to a particularly elegant theory of gravity with torsion, whihc remarkably enough turns out to be an ordinary ...[ SO(2,3) or SO(4,1) Yang-Mills ]... we observe that the cosmological constant must be non-vanishing. ...".
The D4-D5-E6 model coset spaces E6 / (D5 x U(1)) and D5 / (D4 x U(1)) are Conformal Spaces. You can continue the chain to D4 / (D3 x U(1)) where D3 is the 15-dimensional Conformal Group whose compact version is Spin(6), and to D3 / (D2 x U(1)) where D2 is the 6-dimensional Lorentz Group whose compact version is Spin(4). Electromagnetism, Gravity, and the ZPF all have in common the symmetry of the 15-dimensional D3 Conformal Group whose compact version is Spin(6), as can be seen by the following structures with D3 Conformal Group symmetry:
Further, the 12-dimensional Standard Model Lie Algebra U(1)xSU(2)xSU(3) may be related to the D3 Conformal Group Lie Algebra in the same way that the 12-dimensional Schrodinger Lie Algebra is related to the D3 Conformal Group Lie Algebra.
Gravity in the D4-D5-E6 model begins with the Clifford algebra Cl(0,6) = R(8) with spin group Spin(0,6) = SU(4) = compact conformal group of 4-dimensional spacetime. The non-compact conformal group Spin(4,2) = SU(2,2) has the same Clifford algebra R(8) = Cl(4,2), but, to simplify the discussion, the compact group Spin(0,6) will be used in this page.
The conformal group Spin(0,6) = SU(4) is 15-dimensional, with a 10-dimensional subgroup Spin(0,5) = Sp(2) that is the de Sitter group.
The 10 de Sitter infinitesimal generators correspond to gravitons.
The 15 infinitesimal generators of the conformal group are the 10 Poincare group generators of the de Sitter group plus one scale generator and 4 conformal generators.
Mohapatra (in section 14.6 of Unification and Supersymmetry, 2nd edition, Springer-Verlag 1992) shows that if the scale and conformal gauge degrees of freedom are fixed, then a Lagrangian with the conformal group as gauge group gives the usual Hilbert action for gravity:

After the scale and conformal gauges have been fixed, the conformal Lagrangian becomes a de Sitter Lagrangian. Einstein-Hilbert gravity can be derived from the de Sitter Lagrangian, as was first shown by MacDowell and Mansouri (Phys. Rev. Lett. 38 (1977) 739). (Note that Frank Wilczek, in hep-th/9801184, says that the MacDowell-Mansouri "... approach to casting gravity as a gauge theory was initiated by MacDowell and Mansouri ... S. MacDowell and F. Mansouri, Phys. Rev. Lett. 38 739 (1977) ... , and independently Chamseddine and West ... A. Chamseddine and P. West Nucl. Phys. B 129, 39 (1977); also quite relevant is A. Chamseddine, Ann. Phys. 113, 219 (1978). ...".
Above the 309 MeV energy level, and below the Higgs Vacuum Expectation Value at v = 252 GeV, Gravity looks similar to the Color Force.
Above the Higgs Vacuum Expectation Value at v = 252 GeV: the Higgs mechanism has not taken effect; SU(2) weak bosons and Dirac fundamental fermions are massless; SU(2) gauge symmetry is unbroken; and the strength of Gravity is not so well defined in conventional terms.
For further discussion of the MacDowell-Mansouri mechanism, see Freund (chapter 21 of Introduction to Supersymmetry, Cambridge 1986), or Ne'eman and Regge (Riv. Nuovo Cim. v. 1, n. 5 (1978) 1, at pages 25-28), or Nieto, Obregon, and Socorro, who have shown that the MacDowell-Mansouri Spin(0,5) = Sp(2) de Sitter Lagrangian for gravity used in the D4-D5-E6 model plus
a Pontrjagin topological term
the Lagrangian for gravity in terms of the Ashtekar variables
a cosmological constant term - which may vary during Expansion of the Instanton Universe,
Aldrovandi and Pereira, in gr-qc/9809061, show that de Sitter groups of the MacDowell-Mansouri Gravity mechanism can describe Special Relativity in SpaceTimes with varying Cosmological Constant. They use Inonu-Wigner contractions of de Sitter groups and spaces to show that in a weak cosmological constant limit the de Sitter groups are contracted to the Poincare group, and the de Sitter spaces are reduced to the Minkowski space, while in the strong cosmological-constant limit the de Sitter groups are contracted to another group which has the same abstract Lie algebra of the Poincare group, and the de Sitter spaces are reduced to a 4-dimensional cone-space of infinite scalar curvature, but vanishing Riemann and Ricci curvature tensors, in which the special conformal transformations act transitively and the equivalence between inertial frames is that of special relativity. If the fundamental spacetime symmetry of the laws of Physics is that given by the de Sitter instead of the Poincare group, the P-symmetry of the weak cosmological constant limit and the Q-symmetry of the strong cosmological constant limit can be considered as limiting cases of the fundamental symmetry. Minkowski and the cone-space can be considered as dual to each other, in the sense that their geometries are determined respectively by vanishing and infinite cosmological constants. The same can be said of their kinematical group of motions.
an Euler topological term - which counts the number of handles of a maniforld and for 4-dim spacetime is a 4-form that is proportional to the square root of the determinant of the 4x4 matrix representing the curvature 2-form (see sec. 11.4 of Nakahara, Geometry, Topology, and Physics, Adam Hilger 1990).
If you look at the chain of the 6-dim Lorentz Group Spin(4) included in the 10-dim de Sitter Spin(5) included in the 15-dim Conformal Spin(6), you see that:
the 5 dimensions of Spin(6) outside Spin(5) are gauge-fixed Conformal transformations and fixed Scale transformation; and
the 4 dimensions of Spin(5) outside Spin(4) (de Sitter/Poincare translations) combine to form the Metric of Einstein Gravity.
What about the 6 Lorentz Spin(4) dimensions? As Freund (chapter 21 of Introduction to Supersymmetry, Cambridge 1986) says, they "... do not propagate, they are composite fields. ...".
They are the 3 spatial rotations and 3 Lorentz boosts of the 4 vierbein basis vectors of 4-dim Spacetime, which basis vectors can be represented as the 4 future links of a 4-dimensional HyperDiamond Lattice.
Each of the 4 past links is the time-reversal negative of one of the 4 future links.
It is interesting to note that if you look at the permutation group of the 4 future links, S4 with 4! = 24 elements, you see that it is the Weyl Group of the A3 = D3 Lie Algebra of the compact Conformal Group SU(4) = Spin(0,6), with noncompact form SL(4) = Spin(2,4), which is where we started in constructing the D4-D5-E6 model theory of Gravity. It is also interesting that the 24 elements of S4 are in 1-1 correspondence with the 24 root vectors of the D4 Lie Algebra of Spin(0,8) used in constructing the entire D4-D5-E6 model.
In the D4-D5-E6-E7-E8 VoDou Physics model, Gravity and the Cosmological Constant come from the MacDowell-Mansouri Mechanism and the 15-dimensional Spin(2,4) = SU(2,2) Conformal Group, which is made up of:
According to gr-qc/9809061 by R. Aldrovandi and J. G. Peireira:
"... By the process of Inonu&endash;Wigner group contraction with R -> oo ...[where R ]... the de Sitter pseudo-radius ... , both de Sitter groups ... with metric ... (-1,+1,+1,+1,-1) ...[or]... (-1,+1,+1,+1,+1) ... are reduced to the Poincare group P, and both de Sitter spacetimes are reduced to the Minkowski space M. As the de Sitter scalar curvature goes to zero in this limit, we can say that M is a spacetime gravitationally related to a vanishing cosmological constant.On the other hand, in a similar fashion but taking the limit R -> 0, both de Sitter groups are contracted to the group Q, formed by a semi&endash;direct product between Lorentz and special conformal transformation groups, and both de Sitter spaces are reduced to the cone&endash;space N, which is a space with vanishing Riemann and Ricci curvature tensors. As the scalar curvature of the de Sitter space goes to infinity in this limit, we can say that N is a spacetime gravitationally related to an infinite cosmological constant.
If the fundamental spacetime symmetry of the laws of Physics is that given by the de Sitter instead of the Poincare group, the P-symmetry of the weak cosmological&endash;constant limit and the Q-symmetry of the strong cosmological&endash;constant limit can be considered as limiting cases of the fundamental symmetry.
Minkowski and the cone&endash;space can be considered as dual to each other, in the sense that their geometries are determined respectively by a vanishing and an infinite cosmological constants. The same can be said of their kinematical group of motions: P is associated to a vanishing cosmological constant and Q to an infinite cosmological constant.
The dual transformation connecting these two geometries is the spacetime inversion x^u -> x^u / sigma^2 . Under such a transformation, the Poincare group P is transformed into the group Q, and the Minkowski space M becomes the cone&endash;space N. The points at infinity of M are concentrated in the vertex of the cone&endash;space N, and those on the light&endash;cone of M becomes the infinity of N. It is interesting to notice that, despite presenting an infinite scalar curvature, the concepts of space isotropy and equivalence between inertial frames in the cone&endash;space N are those of special relativity. The difference lies in the concept of uniformity as it is the special conformal transformations, and not ordinary translations, which act transitively on N. ...
... in the light of the recent supernovae results ... favoring possibly quite large values for the cosmological constant, the above results may acquire a further relevance to Cosmology ...".
Since the Cosmological Constant comes from the 10 Rotation, Boost, and Special Conformal generators of the Conformal Group Spin(2,4) = SU(2,2), the fractional part of our Universe of the Cosmological Constant should be about 10 / 15 = 67%.
Since Black Holes, including Dark Matter Primordial Black Holes, are curvature singularities in our 4-dimensional physical spacetime, and since Einstein-Hilbert curvature comes from the 4 Translations of the 15-dimensional Conformal Group Spin(2,4) = SU(2,2) through the MacDowell-Mansouri Mechanism (in which the generators corresponding to the 3 Rotations and 3 Boosts do not propagate), the fractional part of our Universe of Dark Matter Primordial Black Holes should be about 4 / 15 = 27%.
Since Ordinary Matter gets mass from the Higgs mechanism which is related to the 1 Scale Dilatation of the 15-dimensional Conformal Group Spin(2,4) = SU(2,2), the fractional part of our universe of Ordinary Matter should be about 1 / 15 = 6%.
Therefore, our Flat Expanding Universe should, according to the cosmology of the D4-D5-E6-E7-E8 VoDou Physics model, have, roughly:
In my opinion,
WMAP observation of the Cosmic Background Radiation indicates that live in a Flat Expanding Universe with three types of stuff:
cold dark matter (such as black holes,ranging in size from the stable Planck mass to Jupiter mass, and possibly some gravitational interactions from other Worlds of the Many-Worlds) - 23% ; and
a Cosmological Constant L(t) - 73% .
The ratio of the Cosmological Constant to Dark Matter plus Ordinary Matter is the ratio of the number of the 10 Spin(2,3) = Sp(2) generators
that involve time ( and therefore evolution/expansion of the universe and therefore the Cosmological Constant ), which is 3 boosts plus 4 translations ( purely spacelike translations being a set of measure zero, as most translations have some time component ), or 7
to the number of them
that are fixed in time, which is 3 rotations.
Therefore, our Flat Expanding Universe should have:
Dark Matter plus Ordinary Matter - 30%.
Since Ordinary Matter gets mass from the Higgs mechanism which is related to the 1 Scale Dilatation of the 15-dimensional Conformal Group Spin(2,4) = SU(2,2), while Dark Matter Primordial Black Holes are related to its 4 Special Conformal Transformations, the ratio of Ordinary Matter to Dark Matter Primordial Black Holes should be 1 to 4, so that our Flat Expanding Universe should, according to the cosmology of the D4-D5-E6-E7-E8 VoDou Physics model, have:
In my opinion,
Garcia-Compean, Obregon, and Ramirez have shown that the Pontrjagin term is a THETA term, so that they can construct a dual theory associated with the MacDowell-Mansouri theory.
The self-dual MacDowell-Mansouri theory corresponds to the Ashetekar self-dual spin connection formalism and the approach of Nieto, Obregon, and Socorro.
When the anti-self-dual part (and the THETA term) are also taken into account, it appears that it is possible that Gravitational Monopoles and/or Gravitational Solitons can be constructed.
Garcia-Compean, Obregon, and Ramirez use the group SO(3,2) in their paper. They note that, following the 1978 work of MacDowell and Mansouri, Heinz Pagels (Phys. Rev. D 29 (1984) 1690) used the group O(5) to get a Euclidean formulation similar to the MacDowell-Mansouri theory.
A Pontrjagin topological term for 4-dim spacetime is proportional to the trace of the square of the 4x4 matrix representing the curvature 2-form (see sec. 11.4 of Nakahara, Geometry, Topology, and Physics, Adam Hilger 1990). It may correspond to creation and expansion of an Instanton Universe.
Medina and Nieto have shown that the Pontrjagin term may be related to Chern-Simons theory for gauge group Spin(2,3), which in turn may be related to conformal field theory in 1+1 dimensions. Smolin has surveyed the Crane ladder of dimensions going from 3+1 dimensions to 2+1 (Chern-Simons topological theory with massive gravitons) to 1+1 (WZW conformal field theory). Smolin says that the ladder is related to the holographic hypothesis of 't Hooft and Susskind that a quantum field theory on the interior of a black hole is best described by a quantum field theory on its boundary.
What is the physical reason for fixing the scale and conformal degrees of freedom?
In the D4-D5-E6 model, the answer to that question comes from the answer to another question:
Since all rest mass comes from the Higgs mechanism, and since rest mass interacts through gravity, what is the relationship between gravity and the Higgs mechanism?
As remarked by Sardanashvily, Heisenberg and Ivanenko in the 1960s made the first atttempt to connect gravity with a symmetry breaking mechanism by proposing that the graviton might be a Goldstone boson resulting from breaking Lorentz symmetry in going from flat Minkowski spacetime to curved spacetime.
Sardanashvily (see also gr-qc/9405013, gr-qc/9407032, and gr-qc/9411013)
proposes that gravity be represented by a gauge theory with group GL(4), that GL(4) symmetry can be broken to either Lorentz SO(3,1) symmetry or SO(4) symmetry, and that the resulting Higgs fields can be interpreted as either the gravitational field (for breaking to SO(3,1) or the Riemannian metric (for breaking to SO(4). The identification of a pseudo-Riemannian metric with a Higgs field was made by Trautman (Czechoslovac Journal of Physics, B29 (1979) 107), by Sardanashvily (Phys. Lett. 75A (1980) 257), and by Ivanenko and Sardanashvily (Phys. Rep. 94 (1983) 1). In gr-qc/9711043, Sardanashvily has constructed a composite spinor bundle such that any Dirac spin structure is its subbundle and such that the composite spinor bundle admits general covariant transformations. Sardanashvily's Clifford algebra structure should allow treatment of the interaction between spinors and gravity to be represented by curvature in a Clifford Manifold as done by William Pezzaglia in gr-qc/9710027 in his derivation of the Papapetrou Equations.
In the D4-D5-E6 model (using here the compact version) the conformal group Spin(0,6) = SU(4) is broken to the de Sitter group Spin(0,5) = Sp(2) by fixing the 1 scale and 4 conformal gauge degrees of freedom.
The resulting Higgs field is interpreted in the D4-D5-E6 model as the same Higgs field that gives mass to the SU(2) weak bosons and to the Dirac fermions by the Higgs mechanism.
The Higgs mechanism requires "spontaneous symmetry breaking" of a scalar field potential whose minima are not zero, but which form a 3-sphere SU(2). In particular, one real component of the complex Higgs scalar doublet is set to v / sqrt(2), where v is the modulus of the 3-sphere of minima, usually called the vacuum expectation value.
If the 3-sphere is taken to be the unit quaternions, then the "spontaneous symmetry breaking" requires choosing a (positive) real axis for the quaternion space.
In the standard model, it is assumed that a random vacuum fluctuation breaks the SU(2) symmetry and in effect chooses a real axis at random.
In the D4-D5-E6 model, the symmetry breaking from conformal Spin(0,6) to de Sitter Spin(0,5) by fixing the 1 scale and 4 conformal gauge degrees of freedom is a symmetry breaking mechanism that does not require perturbation by a random vacuum fluctuation.
Gauge-fixing the 1 scale degree of freedom fixes a length scale. It can be chosen to be the magnitude of the vacuum expectation value, or radius of the SU(2) 3-sphere.
Gauge-fixing the 4 conformal degrees of freedom fixes the (positive) real axis of the SU(2) 3-sphere consistently throughout 4-dimensional spacetime.
Therefore, the D4-D5-E6 model Higgs field comes from the breaking of Spin(0,6) conformal symmetry to Spin(0,5) de Sitter gauge symmetry, from which Einstein-Hilbert gravity (with Torsion) can be constructed by the MacDowell-Mansouri mechanism.
"... The Einstein-Cartan theory of gravitation and the classical theory of defects in an elastic medium are presented and compared. The former is an extension of general relativity and refers to four-dimensional space-time, while we introduce the latter as a description of the equilibrium state of a three-dimensional continuum. Despite these important differences, an analogy is built on their common geometrical foundations, and it is shown that a space-time with curvature and torsion can be considered as a state of a four-dimensional continuum containing defects. ... torsion refers to the non-symmetric part of the affine connection in a manifold, and in general relativity the torsion is assumed to be zero. ... From a physical point of view, torsion in ECT is generated by the spin. Hence, in ECT, both mass and spin, which are intrinsic and fundamental properties of matter, influence the structure of space-time. ...... we want to introduce the concept of torsion by illustrating its use in the theory of defects, where curvature and torsion are used to describe the geometric properties of a material continuum. ... the Einstein-Cartan theory of gravitation and the theory of defects have similar fundamental equations, and we shall stress the analogies and differences in their underlying geometric structure. ...
... Trautman ... introduced a characteristic length to estimate the effects of torsion, the "Cartan" radius. To achieve the condition ...[that] spin effects ... be of the same order as mass effects ... or, alternatively, when the matter density is [about] 10^47 g cm^(-3) for electron-like matter and 10^54 g cm^(-3) for nucleon-like matter, ... we can imagine that a nucleon of mass m should be squeezed so that its radius coincides with the Cartan radius r_Cart ... For a nucleon we obtain r_Cart = 10^(-26) cm, which is very small when compared with macroscopical scales, but it is larger than the Planck length. Hence, torsion must be taken into account to achieve a quantum theory of gravity. ...
... formally, the Einstein-Cartan field equations describe the defect state of a three-dimensional continuum, at least when the defects are small so that we can use a linear approximation. The analogy is completed by the conservation equations, which, stated as geometric identities, give the correct conservation laws for dislocations and disclinations. ... Now we ask if we start from this three-dimensional correspondence in the linearized theory, is it possible to say something about the 3 + 1 space-time situation? ... When passing from 3 to 4 dimensions, there is an important difference in the geometric description of the medium. In three dimensions we can say that the effect of disclinations is to produce curvature. We used the Einstein tensor Gij to write the incompatibility equation, but we did not say explicitly that the curvature tensor and the Einstein tensor are equivalent. It is well known that in three dimensions they have the same number of independent components, which means that when the curvature tensor is zero, the Einstein tensor also is zero and vice versa. The presence of defects produces a nontrivial Einstein tensor, which also means that the curvature tensor is not zero. The same correspondence does not hold in four (or more) dimensions, because we can have curvature even if the Einstein tensoris zero. In particular, far from the sources, the curvature tensor could be nonzero. Indeed, this happens also in general relativity, because space-time is curved even far from the sources. If we extend the analogy to a four-dimensional context, we should expect that the effects of defects propagate through the manifold and are not purely local, as in three dimensions.
Kleinert ... adopted a linearized approach and showed that space-time with torsion and curvature can be generated from a flat space-time using "singular coordinate transformations," and is completely equivalent to a medium filled with dislocations and disclinations. In other words his singular coordinate transformations are the space-time equivalent of the plastic deformations which lead to incompatible states ... Hence, at least in this approximation, space-time can be thought of as a defect state, and defects are nothing but mass, mass current, and spin. The next important point is to try to go beyond the linear approximation.
We did our previous comparisons assuming small defects in order to use a linearized theory. As we have said, this assumption is fundamental for defining a density of disclinations. We must consider also that in real bodies there are physical constraints on the size of defects: additional or missing matter should not be such as to produce cracks in the structure. Hence, from a phenomenological point of view, it is often suffcient to use a linear theory, as it usually the case for the elastic theory of defects, where the linear Hooke's law is used.
However, curvature and torsion can always be introduced geometrically by the parallel transport procedure ... No approximation is contained in the equations governing curvature and torsion, so from the viewpoint of a geometric treatment no linearization is needed. ...
... four-dimensional equations which characterize the state of the medium ...[are]... a nonlinear generalization of the incompatibility equation, and ... the proportionality between torsion and the dislocation tensors. ... The correspondence between ...[them]... and ... the Einstein-Cartan field equations ... is obtained ...[for the proportionality between torsion and the dislocation tensors by]... using the definition of the Palatini tensor ...
... We can then say that Einstein-Cartan space-time can be considered as a defect state of a four-dimensional continuum, and the equations that describe the dynamical properties of this continuum correspond to the incompatibility equation and torsion source equation for space-time. This correspondence is an interesting analogy for the Einstein- Cartan theory. The meaning of the analogy becomes clear on physical grounds when we use three-dimensional equations in a linear theory of defects, where we have seen that the dislocation density is analogous to the moment stress tensor, and the total density of defects is analogous to the force stress tensor. ... In this analogy, the Poincare group, which is defined by the semidirect product P(10) = SO(1,3) x T(4), takes the place of the Euclidean group of R3. In this case we have six kinds of disclination-like deformations, and four kinds of dislocation-like deformations, which yield 10 different Riemann-Cartan spaces filled with topological defects. ... a Burgers vector B in T (4) and a Frank matrix G in SO(1,3) are defined by the parallel transport of a tetrad in the Riemann-Cartan space U4 around the line-like defect region. In this way, a space-time with curvature and torsion is thought of as a distorted medium filled with dislocations and disclinations ...".
The physical 4-dimensional SpaceTime of the D4-D5-E6-E7-E8 VoDou Physics model is a 4-dimensional HyperDiamond lattice SpaceTime that is continuously approximated globally by RP1 x S3 and locally by Minkowski SpaceTime, with Gravity coming from the 15-dimensional Conformal Group Spin(2,4) by the MacDowell-Mansouri mechanism. The curved SpaceTime of General Relativity is not considered fundamental, but is produced by by starting with a linear spin-2 field theory of massless gravitons in flat spacetime, and then adding higher-order terms to get Einstein-Hilbert gravity (without a cosmological constant - to get a cosmological constant, use massive spin-2 gravitons). The observed curved spacetime is therefore based on an unobservable flat spacetime.
Richard Feynman's book Lectures on Gravitation (1962-63 lectures at Caltech), Addison-Wesley 1995, contains a section on Quantum Gravity by Brian Hatfield, who says: "... Feynman ... felt ... that ... the fact that a massless spin-2 field can be interpreted as a metric was simply a "coincidence" ... In order to produce a static force and not just scattering, the emission or absorption of a single graviton by either particle [of a pair of particles] must leave both particles in the same internal state ... Therefore the graviton must have integer spin. ... when the exchange particle carries odd integer spin, like charges repel and opposite charges attract ... when the exchanged particle carries even integer spin, the potential is universally attractive ... If we assume that the exchanged particle is spin 0, then we lose the coupling of gravity to the spin-1 photon ... the graviton is massless because gravity is a long ranged force and it is spin 2 in order to be able to couple the energy content of matter with universal attraction ... Hence, the gravitational field is represented by a rank 2 tensor field ... the antisymmetric part behaves like a couple of spin-1 fields ... and therefore should be dumped. This leaves a symmetric tensor field ... the higher spin possibilities are neglected ...".Feynman's book also contains a Foreword by John Preskill and Kip S. Thorne in which they say: "... Feynman's investigations of quantum gravity eventually led him to a seminal discovery ... that a "ghost" field must be introduced into the covariantly quantized theory to maintain unitarity at one-loop order of perturbation theory .... it was eventually DeWitt ... and also Faddeev and Popov ... who worked out how to generalize the covariant quantization of Yang-Mills theory and gravitation to arbitrary loop order ...".
Frank Wilczek, in an article in Physics Today (August 2002, pages 10-11), says: "... There is a perfectly well-defined quantum theory of gravity that agrees accurately with all available experimental data ... A salient difference between how renormalization theory functions in the standard model and how it extends to include gravity is that, whereas in the standard model by itself we need only specify a finite number of parameters to fix all the integrals, after we include gravity we need an infinite number. But that's all right. ... The prescription is to put the coeficients of all nonminimal coupling terms to zero at some reference energy scale ... well below the Planck scale ... the consequences ... are ... far below the limits of observation ...".
Hatfield, in his Quantum Gravity section, also says: "... When a field is quantized, each mode of the field possesses a zero-point energy. Since the field is made up of an infinite number of modes, the vacuum energy of the quantum field is infinite. This infinity is quickly disposed of by normal ordering of the field operators. The justification for doing so is that we are just redefining the zero point of the energy scale which is arbitrary to begin with. However, since gravity couples to all energy, when we add gravity, we can no longer get away with this. ... such a vacuum energy density will appear in a gravity theory as a cosmological constant. ... this is a big problem. ... The hope was that some kind of hidden symmetry ... might render the pure gravity sector of theory finite. However, a computer calculation of two-loop corrections gave a divergent result dashing this hope. ... One way to get improved ultraviolet behavior is to have more symmetry built into a theory. ... One popular approach is called "supergravity" ... based on a symmetry between bosonic and fermionic fields called "supersymmetry." ... Unfortunately, when the dimension of space-time is 4 there still exist potential counterterms (starting at seven loops in the best case). ...". [Note that in the D4-D5-E6-E7-E8 Vodou Physics model, which includes both the standard model and gravity, not just gravity alone, there is a subtle supersymmetry that may give ultraviolet finiteness and solve the problem.]
Preskill and Thorne, in their Foreword, also say: "... the lectures ...[contain]... an unusual approach to the foundations of general relativity ... That appoach ... develops the theory of a massless spin-2 field (the graviton) coupled to the energy-momentum tensor of matter, and demonstrates that the effort to make the theory self-consistent leads inevitably to Einstein's general relativity. ... Feynman was not the very first to make such a claim. ... The field equation for a free massless spin-2 field was written down by Fierz and Pauli in 1939 .... Robert Kraichnan ... studied the problem of deriving general relativity as a consistent theory of a massless spin-2 field in flat space. He described his results in his unpublished 1946-47 Bachelor's thesis ... Kraichnan did not assume that gravity couples to the total energy-momentum tensor ... he derived this result as a consequence of the consistency of the field equatiions. .... Kraichnan continued to pursue this problem at the Institute for Advanced Study in 1949-50. ...he received some encouragement from Bryce DeWitt ... Einstein ... was appalled by an approach to gravitation that rejected Einstein's own hard-won geometrical insights. ... Kraichnan did not publish ... until 1955 ... in a 1954 paper ... Suraj N. Gupta ... proceeds as follows: We wish to construct a theory in which the "source" coupled to the massless spin-2 field h_uv is the energy-momentum tensor, including the energy-momentum of the spin-2 field itself. If the source is chosen to be the energy-momentum tensor 2T^uv of the free field theory (which is quadratic in h), then coupling this source to h_uv induces a cubic term in the Lagrangian. From this cubic term in the Lagrangian, a corresponding cubic term 3T^uv in the energy-momentum tensor can be inferred, which is then included in the source. This generates a quartic term 4T^uv , and so on. The iterative procedure generates an infinite series that can be summed to yield the full nonlinear Einstein equations. ... The first complete version of the argument (and an especially elegant one) was published by Deser in 1970 ...".
Stanley Deser's paper Gen. Rel. Grav. 1 (1970) 9-18 is described in Misner, Thorne, and Wheeler, Gravitation, Freeman 1973, pp. 424-425, where they say: ".... Deser summarizes the analysis at the end thus: "Consistency has therefore led us to universal coupling, which implies the equivalence principle. ... [The] initial flat "background" space is no longer observable." In other words, this approach to Einstein's field equations can be summarized as "curvature without curvature" or - equally well - as "flat spacetime without flat spacetime"! ...".
Preskill and Thorne, in their Foreword, also say: "... Weinberg showed ... From very reasonable assumptions about the analyticity properties of graviton-graviton scattering amplitudes ... that the theory of an intereacting massless spin-2 particle can be Lorentz invariant only if the particle couples to matter (including itself) with a universal strength; in other words, only if the strong principle of equivalence is satisfied. ... Once the principle of equivalence is established, one can proceed to the construction of Einstein's theory ...".
Steven Weinberg, in his book Gravitation and Cosmology (Wiley 1972), says in his Preface: "... I believe that the geometrical approach has driven a wedge between general relativity and the theory of elementary particles. ... the passage of time has taught us not to expect that the strong, weak, and electromagnetic interactions can be understood in geometrical terms, and too great an emphasis on geometry can only obscure the deep connections between gravitation and the rest of physics. In place of Riemannian geometry, I have based the discussion of general relativity on a principle derived from experiment: the Principle of Equivalence of Gravitation and Inertia. ... Riemannian geometry appears only as a mathematical tool for the exploitation of the Principle of Equivalence, and not as a fundamental basis for the theory of gravitation. ...".
If you were to start, not with locally Minkowski SpaceTime, but with the curved SpaceTime of General Relativity, then you would see that the Conformal transformations of Minkowski SpaceTime by the 15-dimensional Conformal Group Spin(2,4) corresponds to the Conformal transfomations of the curved SpaceTime by the infinite-dimensional Conformal subgroup of the group Diff(M4) of General Relativistic coordinate transformations of the 4-dimensional SpaceTime M4 of General Relativity, which Conformal subgroup is defined as those General Relativistic coordinate transformations that preserve conformal structure and which infinite-dimensional Conformal subgroup can be called the Weyl Conformal Group. (See Ward and Wells, Twistor Geometry and Field Theory, Cambridge 1991, p. 261.)
To study the curvature of 4-dimensional curved metric SpaceTime (see Misner, Thorne, and Wheeler, Gravitation, Freeman 1973), start with the 256 = 4^4 component tensor Rabcd, and then impose the symmetries required by curvature Rabcd = R[ab][cd] = R[cd][ab] and R[abcd] = 0 and Ra[bcd] = 0 to see that the Riemann curvature tensor Rabcd has 20 independent components. Then decompose Rabcd into the 10-component symmetric Ricci tensor Rab and the 10-component conformal traceless Weyl tensor Cabcd. Then the Einstein tensor Gab is given by Gab = Rab - (1/2)R, where R is the scalar curvature. The Riemann tensor Rabcd obeys the Bianchi identities, and the Einstein tensor Gab is the only contraction that obeys contracted Bianchi identities, which geometrically mean that the boundary of a boundary is zero. To see the Riemann, Ricci, and conformal Weyl tensors written in terms of spinors or twistors, see Penrose and Rindler, Spinors and Space-Time, vols. 1 and 2, Cambridge 1986. Penrose (The Emperor's New Mind, Oxford 1989) describes the Ricci tensor as measuring volume, while the Weyl tensor measures tidal distortion, so that Ricci is a source like electric charges and currents, but Weyl is like the electromagnetic field that carries waves of radiation.
If you were to formulate the Conformal Gravity and Higgs structures of Sardinashvily by starting with the curved metric SpaceTime of General Relativity, you would replace the 15-dimensional Conformal Group Spin(2,4) with the infinite-dimensional Weyl Conformal Group, and you might get something very much like the Proper Time Dynamics in General Relativity and Conformal Unified Theory of Gyngazov, Pawlowskiy, Pervushinz, and Smirichinski in gr-qc/9805083. In their model, as in the D4-D5-E6 model, the Lagrangian has two sectors that are linked by the Higgs mechanism: a Gravitational Sector that acts to curve physical SpaceTime with characteristic energy that is the energy of the Planck Mass; and a Standard Model Sector that acts on Internal Symmetry Space with characteristic energy that is the energy of the Proton Mass. As Gyngazov, Pawlowski, Pervushin, and Smirichinski say, "... Roughly speaking Planck Mass is nothing but a multiplicity of the proton mass. ...", and as the D4-D5-E6 model says, the Planck Mass / Proton Mass ratio is on the order of 10^19.
The Conformal Unified Theory of Gyngazov, Pawlowski, Pervushin, and Smirichinski contains spinor particles, such as neutrinos. SpaceTime transformations of spinors produce torsion displacement in the 4th dimension if you go around a spatial loop that ends at the beginning spatial point. Gravity with torsion comes from the Cartan point of view of varying the connection as an independent variable as well as the metric, which is varied in the Einstein point of view. From the Cartan point of view, torsion does not propagate and its coupling to spin is of the magnitude of the Gravitational Constant G (Gockeler and Schucker, Differential Geometry, Gauge Theories, and Gravity, Cambridge 1987, p. 71, and Freund, Supersymmetry, Cambridge 1986, p. 104-105). Conformal Weyl curvature is discussed in relation to torsion and spin in the book of Buchbinder, Odintsov, and Shapiro, Effective Action in Quantum Gravity (IOP 1992).
Donoghue has shown a way to formulate gravity as an effective field theory at low energies. He has also written a shorter survey article.
In their book Gravitation (W. H. Freeman 1973), Misner, Thorne, and Wheeler say (at pages 380, 378, 420-423):
"... Identify the stress-energy tensor (up to a factor of ... 8 pi G / c^4 ...) with the moment of rotation ... the conservation of moment of rotation follows from ...
(1) The moment of rotation associated with any elementary 3-cube is by definition a net value, obtained by adding the six moments of rotation associated with the six faces of that cube.
(2) When one sums these net values for all 8 3-cubes ... which are the boundary of the elementary 4-cube ...[
]... one counts the contribution of a given 2-face twice, once with one sign and once with the opposite sign. In virtue of the principle that "the boundary of a boundary is zero," the conservation of moment of rotation [ and of stress-energy ] is thus an identity. ...
"Mass-energy curves space" is the central principle of gravitation. ...
"Space" means spacelike hypersurface. ...
the scalar curvature ... of the 3-geometry intrinsic to the [ spacelike ] hypersurface ... is defined by ... measurements of distance made within the hypersurface ...
the "extrinsic curvature" of this 3-geometry relative to the 4-geometry of the enveloping spacetime ... "how curved one cuts his slice" ...
"curvature of space" must (1) be a single number ( a scalar ) that (2) depends on the inclination ... of the cut one makes through spacetime ... in constructing the hypersurface ... but (3) must be unaffected by how one curves his cut. ...
All of Einstein's geometrodynamics is contained in this statement ...
= Intrinsic Curvature Scalar + Extrinsic Curvature Scalar =
= 16 pi ( Local Density of Mass-Energy )
... [ which is ] valid for every spacelike slice through spacetime at any arbitrary point ...
The factor 16 pi is appropriate for the ... system of units ... density ... in cm^(-2) given by
multiplied by the density ... expressed in ... g / cm^3 ...".
In Lecture 11.2 of his Feynman Lectures on Gravitation (Addison-Wesley 1995), at page 154, Richard Feynman says:
"... we may give an interpretation of the theory of gravitation ... as follows: ... Consider a small three-dimensional sphere ... [ in a ] three-space perpendicular to the time axis ... Its actual radius exceeds the radius calculated by Euclidean geometry ... by an amount proportional ... [ by the factor ] G / 3 c^2 ... to the amount of matter inside the sphere ... one fermi per 4 billion metric tons ... we require the same result to hold in any coordinate system regardless of its velocity. ...".
1 that scales/dilates spacetime, whose action is like just expanding or contracting space at a single given point, and its action is suppressed because of Feynman's factor of G / 3 c^2 that is of the order of about 10^(-28); and
4 that do special conformal transformations, which have some global nonlocal effects
by which they can expand space at one point and produce a corresponding contraction of space at another point. Their effects are globally conservative in that there is no total net input or output of energy.
In astro-ph/9707165, Lasenby, Doran, Dobrowski, and Challinor say:
"... Gauge-theory gravity, expressed in the language of Geometric Algebra [Clifford Algebra],
allows very efficient numerical calculation of photon paths. ... We discuss ... applications of a gauge theory of gravity ... The theory employs [two] gauge fields in a flat Minkowski background spacetime to describe gravitational interactions. ... The first of these, h(a), is a position-dependent linear function mapping the vector argument a to vectors. The position dependence is usually left implicit. Its gauge-theoretic purpose is to ensure covariance of the equations under arbitrary local displacements of the matter fields in the background spacetime. The second gauge field, W(a), is a position-dependent linear function which maps the vector a to bivectors. Its introduction ensures covariance of the equations under local rotations of vector and tensor fields, at a point, in the background spacetime. Once this gauging has been carried out, and a suitable Lagrangian for the matter fields and gauge fields has been constructed, we find that gravity has been introduced. ... the theory is formally similar in its equations (hence local behaviour) to the Einstein-Cartan-Kibble-Sciama spin-torsion theory, but it restricts the Lagrangian type and the torsion type (... torsion that is not trivector type leads to minimally coupled Lagrangians giving non-minimally coupled equations for quantum fields with non-zero spin). ...
If we restrict attention to situations where the gravitating matter has no spin, then there are still differences between general relativity and the theory presented here. These differences arise when time reversal effects are important (e.g. horizons), when quantum effects are important, and when topological issues are addressed. ...
... within the framework of gauge-theory gravity, the Kerr singularity is composed of a ring of matter, moving at the speed of light, which surrounds a disk of pure isotropic tension. ...
... As an interesting aside, we note that self-consistent homogeneous cosmologies, based on a classical Dirac field, require that k = 0 (the universe is spatially flat). ... ".
In the paper Gravity, gauge theories and geometric algebra, downloadable from the web page of The Geometric Algebra Research Group at Cavendish Laboratory, University of Cambridge, Lasenby, Doran, and Gull say: that "...fermionic matter would be able to detect the center of the universe if k=/= 0 [if the univese were not spatially flat] ...".
In the paper Effects of Spin-Torsion in Gauge Theory Gravity, downloadable from the web page of The Geometric Algebra Research Group at Cavendish Laboratory, University of Cambridge, Doran, Lasenby, Challinor, and Gull say: that "... Within [Gauge-Theory Gravity], torsion is viewed as a physical field derived from the gravitational gauge fields. This viewpoint has some conceptual advantages over that used in differential geometry, where torsion is regarded as a property of a non-riemannian manifold. ... for a massive spinning point-particle, moving in a gravitational background with torsion ...the motion is not generally geodesic, the spin vector is not Fermi-transported, and the particle couples to the torsion. ... spinning point particles see a preferred direction in space due to the spin of the matter field. ... with spin there are extra physical fields present which have observable consequences. ...".
In gr-qc/9910099, Chris Doran says: "...
... is global and involves a time coordinate which represents the local proper time for free-falling observers on a set of simple trajectories. ... The Kerr solution ... is global, making it suitable for studying processes near the horizon. ... the time coordinate measured by a family of free-falling observers brings the Dirac equation into Hamiltonian form ... This form of the equations also permits many techniques from quantum field theory to be carried over to a gravitational backgroundwith little modification. ... ".
J. Sladkowski, in gr-qc/9906037, Strongly Gravitating Empty Spaces, says:
"... We use various results concerning isometry groups of Riemannian and pseudo-Riemannian manifolds to prove that there are spaces on which differential structure can act as a source of gravitational force (Brans conjecture). ...[If the] isometry group G of the solution acts nonproperly on R4 ... [then] G is locally isomorphic to SO(n,1) or SO(n,2 ). But the nonproper action of G on R4 means that there are points infinitely close together in R4 ... such that arbitrary large different isometries ... in G maps them into infinitely close points in R4 ... . There must exists quite strong gravity centers to force such convergence (even in empty spacetimes). ...
We see that ... Einstein gravity is quite nontrivial even in the absence of matter. ... Note that we have proven a weaker form of the Brans conjecture: there are four-manifolds (spacetimes) on which differential structures can act as a source of gravitational force just as ordinary matter does. ...".
Note that SO(n,1) and SO(n,2) correspond to Lorentz and Conformal groups, respectively, and their geometry is related to Lie Sphere Geometry and SpaceTime Correlations.
Renormalizable quantum theories are well known for the three forces of the Standard Model (electromagnetism, the weak force, and the color force), and they are part of the D4-D5-E6 model.
The standard model quantum path integral sum over histories breaks the gauge group invariance of the Lagrangian, because the path integral must not overcount paths by including more than one representative of each gauge-equivalence class of paths. The remaining quantum symmetry is the symmetry of BRST cohomology classes. Knowledge of the BRST symmetry tells you which ghosts must be used in quantum calculations, so the BRST cohomology can be taken to be the basis for the quantum theory.
A good description of BRST cohomology is in the paper of Garcia-Compean, Lopez-Romero, Rodriguez-Segura, and Socolovsky. As they state, the only force for which a renormalizable quantum theory is not well known is gravity.
They discuss two current approaches to quantum gravity:
string theory, which abandons point particles even at the classical level; and
redefinition of classical general relativity in terms of new variables, the Ashtekar variables, and trying to use the new variables to construct a quantum theory of gravity.
Nieto, Obregon, and Socorro have shown that the MacDowell-Mansouri Spin(0,5) = Sp(2) de Sitter Lagrangian for gravity used in the D4-D5-E6 model plus
a Pontrjagin topological term
is equal to
the Lagrangian for gravity in terms of the Ashtekar variables plus
a cosmological constant term - which may vary during Expansion of the Instanton Universe, plus
an Euler topological term - which counts the number of handles of a maniforld and for 4-dim spacetime is a 4-form that is proportional to the square root of the determinant of the 4x4 matrix representing the curvature 2-form (see sec. 11.4 of Nakahara, Geometry, Topology, and Physics, Adam Hilger 1990).
A Pontrjagin topological term for 4-dim spacetime is proportional to the trace of the square of the 4x4 matrix representing the curvature 2-form (see sec. 11.4 of Nakahara, Geometry, Topology, and Physics, Adam Hilger 1990). It may correspond to creation and expansion of an Instanton Universe.
Medina and Nieto have shown that the Pontrjagin term may be related to Chern-Simons theory for gauge group Spin(2,3), which in turn may be related to conformal field theory in 1+1 dimensions. Smolin has surveyed the Crane ladder of dimensions going from 3+1 dimensions to 2+1 (Chern-Simons topological theory with massive gravitons) to 1+1 (WZW conformal field theory). Smolin says that the ladder is related to the holographic hypothesis of 't Hooft and Susskind that a quantum field theory on the interior of a black hole is best described by a quantum field theory on its boundary. By using the Crane ladder, you can study black holes with the methods of topological quantum field theory, knot theory, and category theory that are described by Baez in his series This Week's Finds in Mathematical Physics as well as in his books and papers.
Therefore, although the quantum gravity methods of string theory cannot be used in the D4-D5-E6 model because the D4-D5-E6 model uses fundamental point particles at the classical level, methods based on Ashtekar variables are available. Two such approaches are:
a topological approach based on loop groups and spin networks; and
an algebraic approach based on getting BRST transformations from Maurer-Cartan horizontality conditions.
Spin Networks are defined by Baez as "...graphs embedded in a manifold S (the space of spacetime) with edges labelled by representations of a Lie group G and with vertices labelled by intertwining operators. Spin networks define gauge-invariant functions on the space A of connections of any G-bundle over S...".
The intertwining operators are related to the fermion creation and annihilation operators in the 3x3 Octonion Nilpotent Heisenberg Algebra Matrix Model.
The configuration space of gravity using the Ashtekar variables is not the space of metrics, but the space of connections on an SL(2,C) bundle (with compact real form SU(2) = Spin(3)) over S.
The constraints of canonical quantum gravity are then polynomial, and the diffeomorphism constraint is invariance under diffeomorphisms of S. Since loops are invariant under diffeomorphisms of S, and since Wilson loops can represent gauge theories, Rovelli and Smolin proposed a loop representation of quantum gravity.
John Baez, in week 55 of This Week's Finds in Mathematical Physics, discusses work of Rovelli and Smolin and of Loll in which Rovelli and Smolin have shown that the loop representation of quantum gravity is equivalent to an SU(2) Spin Network representation and
Loll has calculated that spatial volume eigenstates of the Spin Network space of states are discrete and nonzero, on the scale of the Planck length, for Spin Networks with at least 4 edges at each vertex.
(Baez says that Rovelli and Smolin made a sign error that led them, in an earlier paper, to conclude that trivalent Spin Networks could have nonzero spatial volume, and that Loll showed at a 1995 Warsaw workshop that trivalent Spin Networks had zero spatial volume, but 4-valent Spin Networks had nonzero Planck-scale spatial volume.)
This leads to the 4-dimensional HyperDiamond Feynman Checkerboard based on the 4-dimensional lattice structure of Michael Gibbs and David Finkelstein.
Gibbs views the 4-dimensional HyperDiamond Feynman Checkerboard as being a lattice in a 4-dimensional spacetime, while Finkelstein developed the Quantum Graphs used in construction of the lattice as a theory of abstract Quantum Graphs not embedded in spacetime, but from which spacetime should be derived.
The D4-D5-E6 model has the discrete structure of the Finkelstein-Gibbs HyperDiamond lattice, and has a gravity sector based on the conformal MacDowell-Mansouri mechanism, which has been shown to be closely related to to the Ashtekar variable picture by Nieto, Obregon, and Socorro.
Baez says that Spin Networks "...were invented in the early 1970s by Penrose ...", and that while the Baez-Rovelli-Smolin-Loll Spin Networks "...involve graphs embedded in a pre-existing manifold that represents space, his [Penrose's] spin networks were abstract graphs ... intended as a purely combinatorial substitute for a spacetime manifold."
Since the Finkelstein-Gibbs 4-dimensional HyperDiamond lattice has spatial structure of the 3-dimensional Diamond lattice, whose natural Spin Network has 4-valent tetrahedral structure, Loll's results support the Finkelstein-Gibbs HyperDiamond Spin Network and the D4-D5-E6 model. As Michael Gibbs says: a 3-valent Spin Network is spatially like 2-dim graphite and a 4-valent Spin Network is spatially like 3-dim diamond.
Barnett and Crane describe Relativistic Spin Networks in terms of the geometry of the 2-dimensional faces of a 4-simplex and the group Spin(4) = SU(2) x SU(2). Crane has extended that model to An Octonionic Geometric State Model also usesthe geometry of a Euclidean 4-simplex and the bivectors on its faces, but, instead of using the group Spin(4) = SU(2) x SU(2), Crane uses the group Spin(8) and its octonionic structure. Crane goes on to"... choose a triangulation of the base manifold, then choose a flat, affine lifting of each 4-simplex to the total space T of the bundle, identified with B4 x R8. This is equivalent to picking a at connection on each 4-simplex. ...". As Crane says, "... Actually, this is only a partial analog of Kaluza-Klein theory, since the variables correspond to a choice of a connection, but not of a metric on the base. ...". Crane then decomposes the 28-dimensional basis { Bij } of Spin(8) into 7 copies of a 4-dimensional Cartan subalgebra whose basis is {B12, B34, B56, B78}, and for which the Spin(8) triality automorphism can be written as
F34 = (1/2) ( - B12 + B34 - B56 - B78)
F56 = (1/2) ( - B12 - B34 + B56 - B78)
F78 = (1/2) ( - B12 - B34 - B56 + B78)
The triality action Fij is the same on each of the 7 copies of the 4-dim Cartan subalgebra; the { Fij } constitute a new basis for the Spin(8) Lie algebra with the same commutation relations as the { Bij }. In the { Fij } basis, the simple bivectors are characterized by |F12| = |F34| = |F56| = |F78|, which suggests a state sum formed by labelling "... each face and each tetrahedron with an irreducible represen tation of Uq(so(8)) whose highest weight satisfied |F12| = |F34| = |F56| = |F78|, join the representations into a 15Jq symbol [as done by Barnett and Crane for Spin(4)], multiply together the evaluations of the 15Jq symbols for all the 4-simplices in the triangulation, normalize with the product of powers of quantum dimensions ..., and sum over labellings. ...we would have to sum over a basis for the tensor operators at each trivalent vertex in our diagrams, since the representation category of so(8) does not have unique tensor operators like the representation category of so(3). ..." Crane predicts that his Octonionic Model has a nonzero cosmological constant and is not chirally symmetric. He suggests that the exceptional Jordan algebra J3(O) and the Lie algebra E6 might be useful in further work on his model.
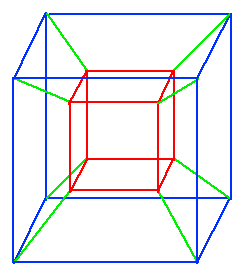
Crane's structure is similar to the structure of the 4-dimensional HyperDiamond Feynman Checkerboard used in the D4-D5-E6 model and in the models of Michael Gibbs and David Finkelstein, whose 4-link future lightcone is a 4-dimensional simplex, with the 4 future ends of the links forming a 3-dimensional tetrahedron. It is shown here, with a stereo pair showing 3 dimensions and color coding (green = present, blue = future) for the 4th dimension.
The 4-link future lightcone leading from a vertex looks a lot like the Quantum Pentacle of David Finkelstein and Ernesto Rodriguez (Int. J. Theoret. Phys. 23 (1984) 887), as well as a lot like an element of the Relativistic Spin Network of Barnett and Crane.
The future tetrahedron, not including the origin vertex, contains 4 vertices and 4 bivector triangles. Those bivectors correspond to the 4 translation bivectors of the 10-dimensional Spin(5) Lie algebra, which is based on the Cl(0,5) Clifford algebra with graded structure 1 5 10 10 5 1, so that there are: 1 empty set, 5 vector vertices, 10 bivector edges, 10 triangles, 5 tetrahedra, and 1 4-simplex. By Hodge duality, the 10 bivector edges correspond to the 10 triangles.
The future lightcone edges leading from the origin are edges on the 6 bivector triangles that include the origin vertex. Those bivectors correspond to the 6 bivectors of the Spin(4) subalgebra of the Spin(5) Lie algebra. The 6-dimensional Spin(4) subalgebra is reducible, isomorphic to SU(2) x SU(2), so that it reduces to 3 rotations and 3 Lorentz boosts. That decomposition is most clearly seen by looking at the dual to the 4-simplex illustrated above, in which its 5 vertices correspond to 5 tetrahedral 3-faces, and vice versa:
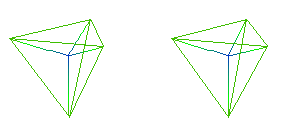
In this dual picture, the 4 vector edges leading from the origin break down into 3 green spacelike vector edges leading from the origin and 1 green-to-blue timelike vector edge leading from the origin. The 3 triangles with 2 spacelike sides correspond to the 3 rotations, and the 3 triangles with 1 spacelike side and 1 timelike side correspond to the 3 Lorentz boosts. As in the original lightcone picture, the 4 triangles that do not include the origin correspond to the 4 translations of the Spin(5) Lie algebra.
Nieto, Obregon, and Socorro have shown that Lagrangian action of the Ashtekar variables is a Chern-Simons action if the Killing metric of the de Sitter group is used instead of the Levi-Civita tensor.
Smolin and Soo have shown that the Chern-Simons invariant of the Ashtekar-Sen connection is a natural candidate for the internal time coordinate for classical and quantum cosmology, so that the D4-D5-E6-E7 model uses Chern-Simons time.
The D4-D5-E6-E7 model has
a quantum theory of the standard model forces (electromagnetism, the weak force, and the color force), and
a quantum theory of MacDowell-Mansouri-Ashtekar gravity.
The two quantum theories must be combined in order to calculate how standard model particles and fields interact in the presence of gravity.
Moritsch, Schweda, Sommer, Tataru, and Zerrouki have done this by using Maurer-Cartan horizontality conditions to get BRST transformations for Yang-Mills gauge fields in the presence of gravity.
This gives a complete quantum structure for the D4-D5-E6-E7 model.
What about the Aether in the D4-D5-E6-E7 model?
My personal opinion is that the Aether is compressible, but only at energies around the Vacuum Expectation Value of the Higgs field, around 250 GeV, which is corrresponds to the Superposition Separation of an entire single Tubulin in the Brain.Since the unit Quaternions form the Lie Group Sp(1) = SU(2) = Spin(3) = S3, Maxwell's use of Quaternions in Electromagnetism anticipated the SU(2) Weak Force and the SU(2)xU(1) ElectroWeak unification, and Maxwell's consideration of a compressible general elastic Aether medium anticipated the Higgs mechanism and Torsion Physics.
In terms of the smallest charged Elementary Particle, the First-Generation Fermion Electron Compton Radius Vortex Particle, the Higgs VEV (about 250 GeV = 5 x 10^5 Me (Electron Masses)) gives the linear compressibility of the Aether,
Therefore, the Gravitational VEV should be given by the 4-volume compressibility of the Aether, so that the Gravitational VEV is about ( 5 x 10^5 )^4 Me = 6 x 10^22 Me = 3 x 10^22 MeV = 3 x 10^19 GeV.
Since the Gravitational VEV should correspond to a pair of Planck Mass Black Holes, the Planck Mass could be derived to be about 1.5 x 10^19 GeV.
......