The volume of about 10^80 Muon or Taun Compton Radius Vortices is roughly the volume of our Universe at the time of the ElectroWeak Phase Transition.

D. Lynden-Bell, in A Magic Electromagnetic Field, astro-ph/0207064, says: "... An electromagnetic field of simple algebraic structure is simply derived. It turns out to be the G = 0 limit of the charged rotating Kerr-Newman metrics. These all have gyromagnetic ratio 2, the same as the Dirac electron. The charge and current distributions giving this high gyromagnetic ratio have charges of both signs rotating at close to the velocity of light. It is conjectured that something similar may occur in the quantum electrodynamic charge distribution surrounding the point electron. ... Classical models of the electron had a problem over the gyromagnetic ratio. Even if all the charge were confined to a ring rotating at close to the velocity of light the magnetic moment generated gives a gyromagnetic ratio of one rather than the electron's value of 2.0023193044. It is of some interest to gain an understanding as to how the Kerr-Newman metric does it. The answer is that the charge distribution is not all of one sign. In fact a circular current dipole of two rings of opposite charge rotating uniformly about their common axis gives a net magnetic moment but no net charge. The way our electromagnetic field gets its large magnetic dipole moment per unit net charge is that its much larger internal charges are of opposite signs but rotate together giving a magnetic dipole with relatively little net charge. We show elsewhere that this is a characteristic of relativistically rotating conductors! ...".
H. I. Arcos and J. G. Pereira, in Kerr-Newman solution as a Dirac particle, hep-th/0210103, say: "... For m^2 < a^2 + q^2 , with m, a, and q respectively the source mass, angular momentum per unit mass, and electric charge, the Kerr-Newman (KN) solution of Einstein's equation reduces to a naked singularity of circular shape, enclosing a disk across which the metric components fail to be smooth. ... similarly to the electron-positron system, this solution presents four inequivalent classical states. ... due to its topological structure, the extended KN spacetime does admit states with half-integral angular momentum. ... under a rotation of the space coordinates, those inequivalent states transform into themselves only after a 4 pi rotation. ... The state vector representing the whole KN solution is then constructed, and its evolution is shown to be governed by the Dirac equation. The KN solution can thus be consistently interpreted as a model for the electron-positron system, in which the concepts of mass, charge and spin become connected with the spacetime geometry. ... for symmetry reasons, the electric dipole moment of the KN solution vanishes identically, a result that is within the limits of experimental data ... a and m are thought of as parameters of the KN solution, which only asymptotically correspond respectively to angular momentum per unit mass and mass. Near the singularity, a represents the radius of the singular ring, which according to Carter is unobservable. The above "renormalization" of the KN parameters ...[is]... necessary to maintain the internal angular momentum constant. As a consequence, to a higher velocity, there might correspond a smaller radius of the singular ring. With this renormalization, it is a simple task to verify that, for the usual scattering energies, the resulting radius is below the experimental limit for the extendedness of the electron. According to these arguments, therefore, the electron extendedness will not show up in high-energy scattering experiments. This extendedness will show up only in low energy experiments, where the electrons move at low velocities. ... Charge ... is interpreted as arising from the multi-connectedness of the spatial section of the KN solution. ... spin can be consistently interpreted as an internal rotational motion of the singular ring. ... this model can provide explanations ...[of]... not well-understood phenomena of solid state physics, as for example the fractional quantum Hall effect. ...".
D. Ranganathan, in A self consistent solution to the Einstein Maxwell Dirac Equations, gr-qc/0306090, says: "... A self consistent solution to Dirac equation in a Kerr Newman space-time with M^2 > a^2 + Q^2 is presented for the case when the Dirac particle is the source of the curvature and the electromagnetic field. The solution is localised, continuous everywhere and valid only for a special choice of ... the parameters (me, Q, a) appearing in the Dirac equation. ... Such a solution corresponds to a generalisation of the free particle Dirac equation in Minkowski space to include the effects of the curvature produced by the particle. The ordinary free particle solutions of the Dirac equation are completely delocalised; the curvature however, now causes the Dirac wave functions to be localised over a region comparable in dimension to the Compton wavelength of the particle. Note that the wave function still has an enormous spread in comparison to the dimensions of the event or Cauchy horizons of the particle. As is usually the case in single particle Dirac theory we ignore the self interaction between the particle and its own electromagnetic field. Further we assume that we need only to look for solutions with zero azimuthal angular momentum about the rotation axis. ... if the fields are centered at r = 0, it is not obvious what it means to have a finite probability of finding the source at r =/= 0. I suggest that this can be explained in a manner similar to the explanation for the Klein paradox of Dirac theory. Namely, in the region of the order of the Compton wavelength within which the wave function peaks, the field strengths are so large that virtual pair creation cannot be neglected. The antiparticle thus produced can recombine with the "original" particle at r = 0 leaving us to detect the particle now at r =/= 0. ... The solution ... is normalisable and thus represents a proper Dirac spinor wave function. There is of course a second possibility due to the bifurcations at the horizon, which is to take the complex conjugate form inside the ergosphere. This however will give rise to the same Dirac currents etc., outside and is thus indistinguishable form the form presented here. Next consider the question of the only allowed energy eigenvalue, zero. In any bound state problem, we expect the energy of the state to be less than or equal to the asymptotic value of the binding potential. In this case if we consider the curvature to be producing the attractive force localising the particle close to r = 0; then the zero energy eigenvalue should evoke no surprise. ...".
Consider this statement by Bert Schroer in hep-th/9908021:
As Streater and Wightman say in PCT, Spin, Statistics, and All That (W. A. Benjamin 1964): "... From Theorem 4-15 [the Jost-Schroer theorem] we get Theorem 4-16 (Haag's Theorem) ... Haag's Theorem is very inconvenient; it means that the interaction picture exists only if there is no interaction. ...".
Schroer goes on to say: "... It is the constructive use of such nonlocal objects which is responsible for the disappearance of the ultraviolet divergency problem and together with it the short-distance aspects of the renormalization problem. ... [Polarization Free Generators] ... generalize the free field structure into a controllable nonlocal direction with interactions, i.e. they are auxiliary quantities in the construction of local theories which exist all the time in the original Hilbert space which is also the living space of the more local operator algebras which they generate. With other words, although they are nonlocal ... and in some sense contain a cut-off aspect, these properties are not ad hoc, and as a consequence no limiting process for cutoff removal is required. Their existence is crucial for the linkage of the particle physics crossing symmetry with the thermal and entropical aspects of QFT which were first noticed in the Bekenstein-Hawking-Unruh properties of Killing horizons in black hole physics. These "classical" thermal properties in CST have a quantum counterpart in which bifurcated Killing horizons are substituted by surfaces of Minkowski space localization regions e.g. the light cone surface of a double cone. In fact the geometric Killing symmetry in the quantum setting passes to the (geometrically) hidden quantum symmetry defined by the modular group corresponding to the concrete situation. In Unruh's case of a wedge region or in the analogous case of conformal matter enclosed in a double cone, the hidden quantum symmetry passes to the one described by a Killing vector associated with the Lorentz or conformal- group. ...".
Further, note that Dirac may have anticipated key aspects of the Compton Radius Vortex model in 1938, as shown in this quote from pages 194-195 of Dirac: A Scientific Biography, by Helge Kragh (Cambridge 1990): "... "... It would appear here that we have a contradiction with elementary ideas of causality. The electron seems to know about he pulse before it arrives and to get up an acceleration (as the equations of motion allow it to do), just sufficient to balance the effect of the pulse when it does arrive." Dirac seemed to accept this pre-acceleration as a matter of fact, necessitated by the equations, and did not discuss it further. However, Dirac explained that the strange behavior of electrons in this theory could be understood if the electron was thought of as an extended particle with a nonlocal interior. He suggested that the point electron, embedded in its own radiation field, be interpreted as a sphere of radius a, where a is the distance within which an incoming pulse must arrive before the electron accelerates appreciably. With this interpretation he showed that it was possible for a signal to be propagated faster than light through the interior of the electron. He wrote: "The finite size of the electron now reappears in a new sense, the interior of the electron being a region of failure, not of the field equations of electromagnetic theory, but of some of the elementary properties of space-time." In spite of the appearance of superluminal velocities, Dirac's theory was Lorentz-invariant. ...".
Gaja/Ganesha Physical Compton Vortex Elementary Particles,
GravitoEM Static Region Gaja/Ganesha Compton Vortex Phenomena, and
GravitoEM Induction Region Gaja/Ganesha Compton Vortex Phenomena.
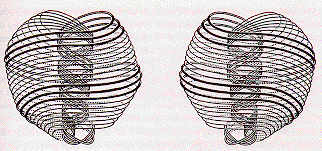
Compton Radius Vortices look like Dolphin Bubble-Structures:

there are superluminal velocities, negative energy solutions (antiparticles), and nonHermitian operators.
In the D4-D5-E6 physics model the electron is a spin 1/2 fundamental particle carrying electromagnetic charge, and the
According to B. G. Sidharth in quant-ph/9808020, quant-ph/9808031, and quant-ph/9805013,
In the usual theory of the Dirac equation the eigenvalues of the velocity operator are +/- the velocity of light while the position operator is non-Hermitian:
The position operator consists of a real part which is the usual position and a rapidly oscillating (or zitterbewegung) imaginary part. This is due to the fact that our measurements are really averaged over time intervals of the order h=mc 2 and correspondingly over the space intervals of the order of h=mc, the Compton wavelength, in which case the imaginary zitterbewegung part disappears. Hermiticity and Conventional Physics begins after the an averaging necessitated by our gross measurements.
The imaginary zitterbewegung position coordinates exist only within the Compton Radius Vortex.
From a classical point of view, within the Compton Radius Vortex v > c is allowed in Lorentz transformations, so that position coordinates within the Compton Radius Vortex become imaginary but outside the Compton Radius Vortex the position coordinates remain real.
Outside the Compton Radius Vortex we have Conventional Physics, but as we approach the Compton Radius Vortex we encounter a region where each of the space time axes becomes a complex plane.
Within the Compton Radius Vortex there are ZPF fluctuations of relativistic virtual ghost particles. Only on averaging over the Compton Radius Vortex do we see only the usual electron moving with subluminal velocities. The De Broglie-Bohm picture of a particle is that of an average over an ensemble; while the Sidharth picture is an averaging over a region that is inaccessible to measurement by Conventional Physics apparatus.
To see how this works, following section 3-7 of J. J. Sakurai's book Advanced Quantum Mechanics (Addison-Wesley 1967), consider that an Electron of mass m is represented outside the Compton Radius Vortex by an oscillatory positive-energy solution in Oscillatory Region I
while within the Compton Radius Vortex the negative-energy Electron solution in Damped Region II is exponentially damped.
The Hydrodynamical Formulation of Bohm Quantum Theory corresponds to the ZPF Fluctuations within the Vortex that effectively produce Short-(Compton Radius)-Range Salam Strong Gravity.
According to Sidharth, a Compton Radius Vortex can be described by the mathematical structure of a Kerr-Newman Black Hole with Spin and Electric Charge, but with a different physical interpretation:
The Compton Radius Vortex interpretation is curvature of SpaceTime by Electromagnetic Charge, ZPF fluctuations, and Spin so great that a region of 4-Real-dimensional SpaceTime becomes
a 4-Complex-dimensional region in which
imaginary zitterbewegung ZPF fluctuation phenomena occur.
is consistent with the Gyromagnetic Ratio of a Kerr-Newman Black Hole.
the ZPF fluctuations of relativistic virtual ghost particles within the Compton Radius Vortex. According to Sidharth, the inertial mass of an elementary particle is the energy of binding of nonlocal amplitudes in the zitterbewegung within the Compton Radius Vortex, which for the Electron has Compton Radius about 10^(-11) cm.
According to Sidharth, the physical origin of rest mass can be seen by analogy with the two-state hydrogen molecular ion. There, the amplitude for the single electron to be with one hydrogen atom or the other shows up as a binding energy.
The energy of the Electron tied up within the Compton Radius Vortex is the inertial mass energy mc^2 . The amplitude for the electron at x to be found at a neighboring point x+b can be taken to the limit in which b approaches the boundary of the Compton Radius Vortex (and not the center 0). The effective mass is then the mass itself!
Therefore, it is the force of binding of nonlocal positions within the Compton Radius Vortex, rather like the Hydrogen molecular ion binding, that manifests itself as inertial mass.
looks like a Kerr-Newman Black Hole as depicted in Black Holes - A Traveller's Guide, by Clifford Pickover (Wiley 1996)
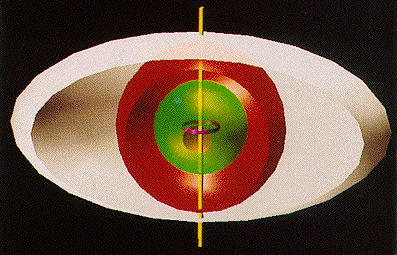
except that
The Ring Singularity (purple) is therefore exposed, and
the hydrodynamic flow of the Bohm Quantum Potential, or, equivalently,
the flow of the ZPF fluctuations of relativistic virtual ghost particles within the Compton Radius Vortex,
is a left-handed vortex flow around the Ring Singularity:
The Compton Radius Vortex illustrations are from clairvoyant viewing by Annie Besant and Charles Leadbeater in 1895, as described in their book Occult Chemistry (ISBN 1-56459-6768-8), and as reprinted in Beyond the Big Bang, by Paul A. Laviolette (Park Street Press 1995). It is very similar to Babbitt's Atom described by Edwin D. Babbitt in his book Principles of Light and Color (1878) (ISBN 0-8065-0748-9). According to a web page of J. Michael McBride "... in the 1860s Lord Kelvin had been suggesting that an atom could be understood as a "vortex" in the "ether" ... Babbitt's "spirillae" are reminiscent of the windings of electromagnetic coils, and his "torrents" look like Faraday's lines of force.... Besant and Leadbeater ...[said]... that "A fairly accurate drawing is given in Babbitt's Principles of Light and Colour, p. 102" ... but they went on to claim: "The illustrations there given of atomic combination are entirely wrong and misleading, but if the stovepipe run through the centre of the single atom be removed, the picture may be taken as correct, and will give some idea of the complexity of this fundamental unit of the physical universe." ...".
The geometry is similar to that of the (3,10) Torus Knot geometry of Stan Tenen.
The Ring Singularity connects Ordinary SpaceTime with Exotic SpaceTime:
To see how a massless (at tree level) Neutrino Compton Radius Vortex compares with a massive Electron Comton Radius Vortex, compare an Electron of mass m as described in section 3-7 of J. J. Sakurai's book Advanced Quantum Mechanics (Addison-Wesley 1967) as being represented outside the Compton Radius Vortex by an oscillatory positive-energy solution in Oscillatory Region I and within the Compton Radius Vortex by an exponentially damped negative-energy Electron solution in Damped Region II
with the m = 0 Neutrino picture
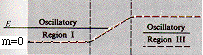
in which the Neutrino is represented outside the Compton Radius Vortex by an oscillatory positive-energy solution in Oscillatory Region I and within the Compton Radius Vortex by an oscillatory negative-energy Neutrino solution in Oscillatory Region III.
the Electron can be "... described by ... the positive energy two spinor and the negative energy two spinor ... under reflection ... [the positive energy two spinor transforms into itself and behaves like a spinor, while the negative energy two spinor transforms into its negative and] ... behaves like a pseudo-spinor; and
the Neutrino "... can be treated as an electron with vanishing mass so that the [Compton Radius Vortex] becomes arbitrarily large. ... [our physical universe is] ... in effect the region within the [Compton Radius Vortex] ... [where] the negative energy [two spinor solution] ... dominates. ... under reflection ... [the negative energy two spinor] ... behaves like a pseudo-spinor [and transforms into its negative] ... [thus giving] ... a rationale for the left handedness of the neutrino. ..."
Since the Compton Radius Vortex is arbitrarily large, Oscillatory Region I does not exist in our physical universe, and the effective picture for the Neutrino is
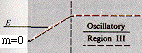
In the D4-D5-E6 physics model, Neutrinos have no Electric (or any other) Charge and have zero tree level Mass. Therefore only the Spin 1/2 of the Neutrino can give it a non-zero Kerr-Newman Radius.
For any finite non-zero Spin J, Mass M = 0 implies that a = J / M is infinite, so that:
the Outer Event Horizon at r = r+ = + sqrt( - a^2 ) is infinite and Complex;
the Inner Event Horizon at r = r- = - sqrt( - a^2 ) is also infinite and Complex;
the Ergosphere at r = + sqrt( - a^2 cos^2(T) ) is infinite and Complex, but with a hole at the poles of the z-axis.
From the point of view of a Neutrino, our entire physical universe is the interior of a Kerr-Newman Black Hole Compton Radius Vortex, so that
Since Neutrinos are Chargeless they do not interact with the Charged ZPF fluctuations of relativistic virtual ghost particles within the Compton Radius Vortex.
Since Neutrinos are tree-level Massless they do not have the non-local Dirac Operator cA.p + Bmc^2 interactions within the Compton Radius Vortex, that is to say, a Neutrino just moves at the speed of light and does not have the massive characteristic of a nonzero amplitude to be at another spatial location.
As J. J. Sakurai says in Advanced Quantum Mechanics (Benjamin/Cummings 1967) (at pages 167-170), the massless character of the Neutrino means that it is not a Dirac particle, but a Weyl particle, so that all Neutrinos are left-handed and all AntiNeutrinos are right-handed.
If a given Neutrino is regarded as a small ball linked by strings to the boundary of its Compton Radius Vortex, then its Spin 1/2 Spinor nature can be directly visualized.
Since Neutrinos see our entire universe as being within a Ring Singularity, it is interesting to speculate that they, interacting among themselves, might be able to travel in macroscopic Closed Timelike Loops.
According to David Kestenbaum's article in Science (281 11 Sep 1998 pp. 1594 - 1595), "... Super-Kamiokande's measurement pins down ... the difference in mass between [electron-type e-neutrinos and muon-type mu-neutrinos] and so indicates only that one of them must have a mass of at least 0.07 electron volts ... earlier experiments had set an upper limit, showing that the electron neutrino, for instance, must have a mass less than 1/30,000 of the electron's. ...". Since the electron mass is about 0.511 MeV = 511 keV = 511,000 eV, the upper limit of the e-neutrino mass is 511,000 / 30,000 = 17 eV.
The Super-Kamiokande results are consistent with the e-neutrino being massless and with the mu-neutrino having a mass of 0.07 eV.
Jack Sarfatti has noted that a mu-neutrino rest mass of 0.07 ev is about 10^-7 the electron mass, so
"... This gives a neutrino Compton wavelength of a micron! Again the size of a living cell! ..."
Therefore, maybe:
Sidharth has "... shown that at the [boundary surface of the Compton Radius Vortex] ... we can deduce [the following equation] ...
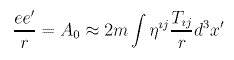 ...
"
...
"As Sidharth notes, referring to Narlikar (in Introduction to Cosmology (2nd ed, Cambridge 1993) at page 57), the Stress-Energy Tensor Tij for particles moving on light-cones (as would the virtual particles of ZPF fluctuations) at unit energy density can be diagonalized to be
1 0 0 0 0 1/3 0 0 Tij = 0 0 1/3 0 0 0 0 1/3
The contribution to electric charge of the T00 component is
1 0 0 0 0 0 0 0 T00 = 0 0 0 0 0 0 0 0
T00 corresponds to the electric charge at distances beyond the boundary of the Compton Radius Vortex, and is only representative of the Electron, which is unconfined (unlike the confined Quarks) and is electrically charged (unlike the electrically neutral Neutrino). T00 corresponds to electric charge of unit magnitude.
At the boundary surface of the Compton Radius Vortex, electric charge corresponds to the terms T11, T22, and T33. The combinations of T11, T22, and T33 are:
0 0 0 0 0 1/3 0 0 T112233 = 0 0 1/3 0 0 0 0 1/3
T112233 corresponds to the Electron whose electric charge has magnitude 1/3 + 1/3 + 1/3 = 1.
0 0 0 0 0 1/3 0 0 T1122-- = 0 0 1/3 0 0 0 0 0
T1122-- corresponds to the Red Up Quark whose electric charge has magnitude 1/3 + 1/3 = 2/3.
0 0 0 0 0 1/3 0 0 T11--33 = 0 0 0 0 0 0 0 1/3
T11--33 corresponds to the Green Up Quark whose electric charge has magnitude 1/3 + 1/3= 2/3.
0 0 0 0 0 0 0 0 T--2233 = 0 0 1/3 0 0 0 0 1/3
T--2233 corresponds to the Blue Up Quark whose electric charge has magnitude 1/3 + 1/3 = 2/3.
0 0 0 0 0 0 0 0 T----33 = 0 0 0 0 0 0 0 1/3
T----33 corresponds to the Red Down Quark whose electric charge has magnitude 1/3.
0 0 0 0 0 0 0 0 T--22-- = 0 0 1/3 0 0 0 0 0
T--22-- corresponds to the Green Down Quark whose electric charge has magnitude 1/3.
0 0 0 0 0 1/3 0 0 T11---- = 0 0 0 0 0 0 0 0
T11---- corresponds to the Blue Down Quark whose electric charge has magnitude 1/3.
0 0 0 0 0 0 0 0 T------ = 0 0 0 0 0 0 0 0
T------ corresponds to the Neutrino whose electric charge has magnitude 0.
Octonion Fermion Triple of
Basis Element Particle SU(2)=Spin(3) Spinors
1 e-neutrino 0 x 0 x 0
i red up quark 1 x 1 x 0
j green up quark 1 x 0 x 1
k blue up quark 1 x 0 x 1
I red down quark 0 x 0 x 1
J green down quark 0 x 1 x 0
K blue down quark 1 x 0 x 0
E electron 1 x 1 x 1

The effective (1+1)-dimensionality of the Pion's constituent Quark and AntiQuark is due to the fact that the Quark and AntiQuark are confined to the Pion and therefore interact at the surface boundaries of their Compton Radius Vortices, so that their Ring Singularities are effectively Naked Singularities with only 1 spatial dimension, that of the Ring Singularity at z = 0 and x^2 + y^2 = a^2.
The Quark and AntiQuark interact as a Breather solution of the (1+1)-dimensional Sine-Gordon equation to form a Pion.
As T. D. Lee says on page 132 of his book Particle Physics and Introduction to Field Theory (Harwood 1981), "... In the special case of the sine-Gordon equation ..., because of the presence of an infinite number of conservation laws, the shape and velocity of each soliton or anti-soliton remain unchanged even after ... a head-on collision. We refer to this special class as indestructible solitons. Indestructible solitons exist only in one space-dimension.
If one requires relativistic invariance, then it exists only for the sine-Gordon equation. ..."
Since the Pion Quark-AntiQuark pair can be thought of as moving on light-cones and being repeatedly annihilated and re-created, the Pion Quark-AntiQuark pair is relativistic, so that the Pion is described as a Sine-Gordon Breather Quark-AntiQuark Pair.
The mass of the Pion, about 140 MeV, is of the same order of magnitude as the characteristic energy, about 245 Mev, of the SU(3) QCD Color Force, and

The Ring Singularities of the Compton Radius Vortices are interconnected like 3 ( red, blue, and green, in the image below ) of the 4 Clifford-Hopf circles of the 24-cell:
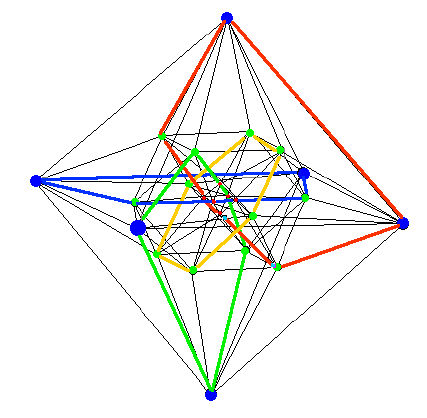
For example, a Proton might have Quark content:
The effective (1+1)-dimensionality of the Proton's constituent Quarks is due to the fact that the Quarks are confined to the Proton and therefore interact at the surface boundaries of their Compton Radius Vortices, so that their Ring Singularities are effectively Naked Singularities with only 1 spatial dimension, that of the Ring Singularity at z = 0 and x^2 + y^2 = a^2.
The 3 Quarks interact as a 3-Soliton solution of the (1+1)-dimensional O(3) model to form a Proton.
As T. D. Lee says on page 132 of his book Particle Physics and Introduction to Field Theory (Harwood 1981), "... because of the presence of an infinite number of conservation laws, the shape and velocity of each soliton or anti-soliton remain unchanged even after ... a head-on collision. We refer to this special class as indestructible solitons. Indestructible solitons exist only in one space-dimension. ..."
As R. Rajaraman says on page 58 of his book Solitons and Instantons (North-Holland 1987), "... The O(3) model is ... interesting in (1+1) dimensions. It has been shown (Pohlmeyer, Comm. Math. Phys. 46 (1976) 207; Luscher and Pohlmeyer, Nucl. Phys. B137 (1978) 46) that, like the sine-Gordon System, the O(3) model in (1+1) dimensions is also characterised by an infinite number of conserved quantities and by Backlund transformations for generating solutions. [In the quantized version of the theory, it has been shown that it is asymptotically free and that the conserved quantities exist free of anomalies (Luscher , Nucl. Phys. B135 (1978) 1; Polyakov, Phys. Lett. 72B (1977) 224).] ... , an exact factorised S-matrix has been constructed using the existence of these infinite conserved quantities (Zamolodchikov and Zamolodchikov, Ann. Phys. (N.Y.) 120 (1979) 253). ... The static solutions ... in (2+1) dimensions ... serve as instantons [in (1+1) dimensions] ... . ... "
T. D. Lee also says on page 132 of his book Particle Physics and Introduction to Field Theory (Harwood 1981), "... If one requires relativistic invariance, then it exists only for the sine-Gordon equation. ..."
Since the Proton has 3 Valence Quarks, and no Valence AntiQuarks, there is no repeated annihilation and re-creation of the Valence Quarks, which are at rest within the confining volume of the Proton because Bohm's "... the PSI-field is able to bring the [3 Valence Quarks] to rest and to transform [their] entire kinetic energy into potential energy of interaction with the PSI-field. ...".
Therefore, the Proton 3-Quark triple is NonRelativistic, so that the relativistic sine-Gordon model is not correct for the Proton, and
At pages 113, 115, and 49, Rajaraman says "... What would happen if we ... directly generalise the O(3) model to N real scalar fields ... [ PHI_n with the sum over n of PHI_n^2 = 1 ? ] ... the allowed values of the field, subject to [ the sum over n of PHI_n^2 = 1 ] ... , now fall on the surface of a hypersphere S(N-1) [in Internal Symmetry Space] ... imbedded in N dimensions. Consequently the holonomy group of localised solutions would now be PI_2(S(N-1)). ... this group is trivial except when N = 3. Consequently non-trivial instanton sectors for the ... O(N) model will exist only when N = 3. ... Consequently, the O(3) model's results cannot be generalized by going to an O(N) model with N greater than 3. (see Din and Zakrewski, Nucl. Phys. B168 (1980) 173) ... the O(3) model in (1+1) dimensions has several interesting properties, many of them similar to the Yang-Mills theory in (3+1) dimensions. Both systems yield instantons characterised by integer-valued toplogical indices. ... both models [are] scale invariant and [yield] instantons of arbitrary size. (At the quantum level, the similarities persist. ... both the O(3) and Yang-Mills theories are renormalisable and asymtotically free.) At the same time, the O(3) model is comparatively simple. It consists of only three scalar fields in its two dimensions with a simple Lagrangian [L given by
where ] ... PHI can be considered as a vector in [Internal Symmetry Space] ... [which is] distinguished from vectors in coordinate space, which are labelled by Lorentz indices, such as [ m in the above equation for L ] ... both the Lagrangian ... and the constraint [ sum over n of PHI_n^2 = 1 ] are invariant under global O(3) rotations in Internal Symmetry Space]. ..."
The mass of the Proton, about 938 MeV, is of the same order of magnitude as the characteristic energy, about 245 Mev, of the SU(3) QCD Color Force, and
Since Spin(3) = SU(2), the 3-real-dimensional Internal Symmetry Space on which O(3) acts in the O(3) Model can be transformed into a 2-complex-dimensional Internal Symmetry Space that is acted upon by SU(2). Since SU(2) acts globally on the symmetric space SU(2) / U(1) = S3 / S1 = S2 = CP1, where CP1 is Complex Projective 1-space. As Rajaraman says on page 116, "... the CP1 model is essentially the same as the O(3) model. ..."
Note about Borromean Rings:
The Borromean Rings image
is from this web page at the Center for the Popularizaton of Mathematics at the University of Wales, Bangor, which page notes "... If you try and make the Borromean Rings out of wire, you will find that you cannot make real flat circles into the figure. There must always be kinks. ... The theorem stating Borromean rings to be impossible with flat circles is proved rigorously in the article "Borromean circles are impossible," Amer. Math. Monthly, 98 (1991) 340-341, by B. Lindstrom and H.-O. Zetterstrom. ... There is another proof ... that flat Borromean circles do not exist, using hyperbolic geometry in four dimensions. ... It is however possible to produce it with ellipses [or rectangles, for which two different axes have different lengths]. ..."
A more elliptical/rectangular set of 3 Borromean Rings can be put in 3 mutually orthogonal planes in 3-dimensional space, as in this image
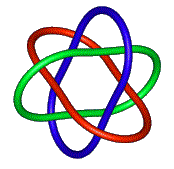
from this web page. The flatter image may not be as accurate, because for rings of finite thickness, Borromean Rings cannot be exactly circular and perfectly flat.
......