Physical interpretations are motivated by Saul-Paul Sirag's ideas about A-D-E, E7, and
as does the McKay Correspondence.
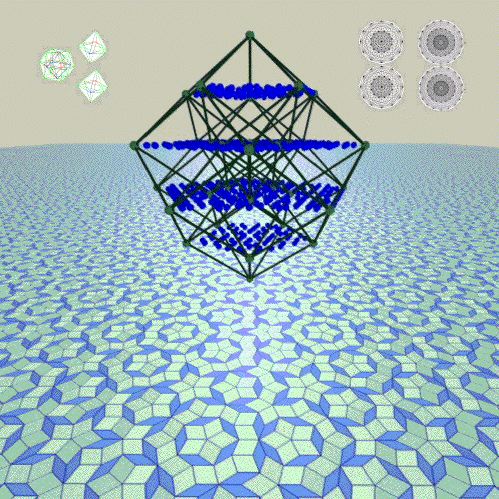
The root vector lattices of the E6-E7-E8 chain of Lie algebras are related to aperiodic Tilings in 2, 3, and 4 dimensions which can be thought of as Irrational Slices of an 8-dimensional E8 Lattice and its sublattices, such as E6. Here is one way to visualize the 240 vertices around the origin of the E8 lattice:

The 2-dimensional Penrose Tiling in the above image was generated by Quasitiler as a section of a 5-dimensional cubic lattice based on the 5-dimensional HyperCube shown in the center above the Penrose Tiling plane.
The above-plane geometric structures in the above image are, going from left to right:
with even part 1 28 70 28 1 and odd part 8 56 56 8
The 0-dimensional polytope formed by a single point with Weyl group the Identity of order 1 corresponds to the Abelian U(1) = Spin(2) With respect to the A-D-E chain of the D4-D5-E6-E7-E8 VoDou Physics model, 1-dimensional A0 = D1 = U(1) is physically the U(1) Electromagnetism Gauge Group. It is in the 12-dimensional Spin(0,8)/U(4) part of D4. Since it is Abelian, it has no Cartan matrix and no Coxeter-Dynkin diagram.
The 1-dimensional polytope formed by the root vectors of the A1 Lie algebra SU(2) = Spin(0,3) = Sp(1) is the 2-vertex line segment
*-------*
with Weyl group 2! = S2 of order 2
With respect to the A-D-E chain of the D4-D5-E6-E7-E8 VoDou Physics model,
3-dimensional A1 = B1 = C1 = SU(2) = Spin(0,3) = Sp(1)
is physically the SU(2) Weak Force Gauge Group.
It is in the 12-dimensional Spin(0,8)/U(4) part of D4.
A Cartan matrix is:
2
The Coxeter-Dynkin diagram is
*
The polytope corresponding to the A1 Lie algebra by The McKay Correspondence is a pair of line segments conecting the two vertices
___ *___*
representing the Cyclic group of order 2. The 2 vertices span 1 dimension so that the 2 vertices in 1 dimension form the Root Vector Diagram of the same A1=B1=C1 Lie algebra.
Since A1=B1=C1 it has 2 root vectors in a 1-dimensional space, its Coxeter Number, the number of root vectors divided by the rank, or dimensionality of its root vector space, is 2 / 1 = 2.
A1=B1=C1 is the basic building block of all Lie algebras, in that any Lie algebra Gn of rank n can be constructed from the root vector space of a Cartesian product of n copies of A1=B1=C1.
If N is the number of root vectors of Gn, its Coxeter number H is H = N / n.
Since 2n of the root vectors of Gn correspond to the Cartesian product of n copies of A1=B1=C1, the excess number of root vectors for each copy of A1=B1=C1 is ( N - 2n ) / n = H - 2.
The extended affine Coxeter-Dynkin diagram is
___ *___*
so that the sum of the nodes (degrees of irreducible representations of the Cyclic group of order 2) is the Coxeter number 2 and the sum of the squares of the nodes (order of the Cyclic group of order 2) is 2.
The 2-dimensional polytope formed by the root vectors of the A2 Lie algebra SU(3) is the hexagon with 6 vertices
/\ ____/__\____ \ / \ / \/ \/ /\ /\ /__\____/__\ \ / \/
with Weyl group 3! = S3 of order 6
(at this stage the permutation group S3 appears,
as we can use reflections through hyperplanes through the origin
to interchange 3 elements of the triangular faces
of the Hexagonal Mogan David);
With respect to the A-D-E chain of the D4-D5-E6-E7-E8 VoDou Physics model,
8-dimensional A2 = SU(3)
is physically the SU(3) Color Force Gauge Group.
It is in the 12-dimensional Spin(0,8)/U(4) part of D4.
A Cartan matrix is:
2 -1
-1 2
The Coxeter-Dynkin diagram is
* | *
The polytope corresponding to the A2 Lie algebra by The McKay Correspondence is a triangle
* / \ *---*
representing the Cyclic group of order 3. The 3-vertex triangle is 2-dimensional, and since there is no 3+2=5-dimensional simple compact Lie algebra, the triangle does not form a Lie algebra Root Vector Diagram.
It has N = 6 root vectors, so its Coxeter number H is H = N / n = 6 / 2 = 3.
The excess number of root vectors for each of the 2 copies of A1=B1=C1 is 3 - 2 = 1.
The extended affine Coxeter-Dynkin diagram is
1 / \ 1---1
so that the sum of the nodes (degrees of irreducible representations of the Cyclic group of order 3) is the Coxeter number 3 and the sum of the squares of the nodes (order of the Cyclic group of order 3) is 3.
The 3-dimensional polytope formed by the root vectors of the D3 Lie algebra Spin(0,6) is the 12-vertex cuboctahedron.
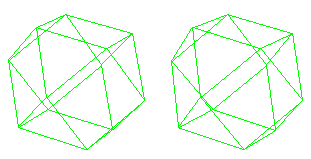
The 12-vertex cuboctahedron of D3 can be constructed from the 4-vertex square Root Vector Diagram of D2 by adding to it
a 4-vertex 2-dim hyperoctahedron cross polytope above in the 3rd dimension, and
a 4-vertex 2-dim hyperoctahedron cross polytope below in the 3rd dimension.
D3 has Weyl group (Z2^2) x 3! = (Z2^2) x S3 of order 24 (the permutation group S3 is present here, as we can use reflections through hyperplanes through the origin to interchange 3 elements of the triangular faces of the cuboctahedron); With respect to the A-D-E chain of the D4-D5-E6-E7-E8 VoDou Physics model, 15-dimensional D3 = A3 = Spin(0,6) = SU(4) has the 10-dimensional structure of Spin(0,5) = Sp(2) that gives physical Gravity from the MacDowell-Mansouri mechanism plus 5-dimensional Spin(0,6) / (Spin(0,5) that gives the conformal structure of the Higgs mechanism. It is in the 16-dimensional U(4) part of D4. The space of Lie Sphere Correlations is a 4-complex-dimensional conformal space D3 / (D2xU(1)) = Spin(0,6) / (Spin(0,4)xU(1)) that is 15-6-1 = 8-real-dimensional. The Shilov boundary related to the 4-complex-dimensional conformal space is 4-real-dimensional RP1xS3. Geometrically, Spin(0,6) / (Spin(0,4) x U(1)) is the set of real projective RP1 spaces in RP5, or, equivalently, the real 2-Grassmannian manifold of R6.
(See Einstein Manifolds, by Arthur L. Besse, Springer-Verlag 1987.)
A Cartan matrix is:
2 0 -1
0 2 -1
-1 -1 2
The Coxeter-Dynkin diagram is
* | *-*
The polytope corresponding to the A3 Lie algebra by The McKay Correspondence is a square
*---* | | *---*
representing the Cyclic group of order 4.
The 4 vertices in the square of 2 dimensions form the Root Vector Diagram of the 4+2=6-dimensional D2 Lie algebra.
The polytope corresponding to the D3 Lie algebra by The McKay Correspondence is a single point that can be thought of as being placed on the 1-dimensional equator of a 2-dimensional sphere S2
*
There are 2 ways to choose the North pole of the 2-sphere S2
and
there are 2 ways (left-handed or right-handed)
to rotate the 2-sphere S2.
Therefore the single point * on the S2 equator
represents the Binary Dihedral group {1,2,2} of order 1x4 = 4,
which can be thought of as a square
*---* | | *---*
since it is isomorphic to the Cyclic group of order 4, and is not isomorphic to the 4-element Dihedral group (2,2,2) that is the Non-Cyclic Klein 4-group.
Here, the brackets () indicate ordinary Dihedral group, and the brackets {} indicate Binary Dihedral group.
It has N = 12 root vectors, so its Coxeter number H is H = N / n = 12 / 3 = 4.
The excess number of root vectors for each of the 3 copies of A1=B1=C1 is 4 - 2 = 2.
The extended affine Coxeter-Dynkin diagram is
1---1 | | 1---1
so that the sum of the nodes (degrees of irreducible representations of the Cyclic group of order 4) is the Coxeter number 4 and the sum of the squares of the nodes (order of the Cyclic group of order 4) is 4.
D3 inherits a non-linear version of triality from the full triality of D4.
the 4-dimensional polytope formed by the root vectors of the D4 Lie algebra Spin(0,8) is the 24-vertex 24-cell.
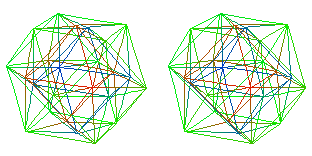
The 24-vertex 24-cell of D4 can be constructed from the 12-vertex cuboctahedron Root Vector Diagram of D3 (green in the figure) by adding to it
a 6-vertex 3-dim octahedron cross polytope (blue in the figure) above in the 4th dimension, and
a 6-vertex 3-dim octahedron cross polytope (red in the figure) below in the 4th dimension.
D4 has Weyl group (Z2^3) x 4! of order 192
Since 8-1 = 7 is the dimension of the imaginary octonions,
Spin(0,8) has octonionic structure and
in fact generates the Lie group Spin(0,8) with fibration
S7 --} Spin(0,8) --} Spin(0,7)
therefore
Spin(0,8) is made up of 4 copies of the imaginary octonions S7.
From the point of view of triality,
Spin(0,8) is made up of 3 copies of the octonions
plus a 4-dimensional root vector space.
With respect to the A-D-E chain of the D4-D5-E6-E7-E8 VoDou Physics model,
28-dimensional D4 = Spin(0,8) has the
16-dimensional structure of U(4)
plus
12-dimensional Spin(0,8) / U(4)
The 16-dimensional U(4) part of D4 = Spin(0,8) has the
1-dimensional structure of a U(1) physical propagator phase
plus the
15-dimensional structure of the A-D-E chain member A3=D3
that is the Spin(0,6) Conformal Group that gives
physical MacDowell-Mansouri Gravity plus the Higgs mechanism.
The 12-dimensional Spin(0,8)/U(4) part of D4 = Spin(0,8) has the
8-dimensional structure of the A-D-E chain member A2
that is physically the SU(3) Color Force Gauge Group
plus
3-dimensional structure of the A-D-E chain member A1=B1=C1
that is physically the SU(2) Weak Force Gauge Group
plus
1-dimensional structure of the A-D-E chain member A0=D1
that is physically the U(1) Electromagnetism Gauge Group
A Cartan matrix is:
2 0 -1 0
0 2 -1 0
-1 -1 2 -1
0 0 -1 2
The Coxeter-Dynkin diagram is
* | *-*-*
The polytope corresponding to the D4 Lie algebra by The McKay Correspondence is a set of 2 points that can be thought of as being placed on the 1-dimensional equator of a 2-dimensional sphere S2.
___ *___*
There are 2 ways to choose the North pole of the 2-sphere S2
and
there are 2 ways (left-handed or right-handed)
to rotate the 2-sphere S2.
Therefore the set of 2 points on the S2 equator
represents the Binary Dihedral group {2,2,2} of order 2x4 = 8,
which is the group of quaternions {+/-1, +/-i, +/-j, +/-k}
that form the 8 vertices of a 16-cell
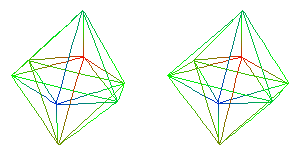
Note that the 4-element Dihedral group (2,2,2) is the Non-Cyclic Klein 4-group.
It has N = 24 root vectors, so its Coxeter number H is H = N / n = 24 / 4 = 6.
The excess number of root vectors for each of the 4 copies of A1=B1=C1 is 6 - 2 = 4.
The extended affine Coxeter-Dynkin diagram is
1 1 \ / 2 / \ 1 1
so that the sum of the nodes (degrees of irreducible representations of {2,2,2}) is the Coxeter number 6 and the sum of the squares of the nodes (order of {2,2,2}) is 8.
J. M. Landsberg has an Algebraic Geometry point of view of D4.
the 5-dimensional polytope formed by the root vectors of the D5 Lie algebra Spin(0,10) has 40 vertices.
The 40-vertex Root Vector Diagram



of D5 can be constructed from the 24-vertex 24-cell Root Vector Diagram of D4 by adding to it
an 8-vertex 4-dim hyperoctahedron cross polytope above in the 5th dimension, and
another 8-vertex 4-dim hyperoctahedron cross polytope below in the 5th dimension.
(The illustration above omits the edges connecting each cross polytope with the 24-cell.)
D5 has Weyl group (Z2^4) x 5! of order 1920 With respect to the A-D-E chain of the D4-D5-E6-E7-E8 VoDou Physics model, 45-dimensional D5 = Spin(0,10) has the 28-dimensional structure of D4 = Spin(0,8) plus U(1) and 8-complex dimensional Spin(0,10) / (Spin(0,8) x U(1)) With respect to the A-D-E chain of the D4-D5-E6-E7-E8 VoDou Physics model, the 8-real-dimensional Shilov boundary S1 x S7 related to the 8-complex dimensional Spin(0,10) / (Spin(0,8) x U(1)) is physically 8-dimensional Spacetime prior to dimensional reduction. Geometrically, Spin(0,10) / (Spin(0,8) x U(1)) is the set of real projective RP1 spaces in RP9, or, equivalently, the real 2-Grassmannian manifold of R10.
(See Einstein Manifolds, by Arthur L. Besse, Springer-Verlag 1987.)
A Cartan matrix is:
2 0 -1 0 0
0 2 -1 0 0
-1 -1 2 -1 0
0 0 -1 2 -1
0 0 0 -1 2
The Coxeter-Dynkin diagram is
* | *-*-*-*
The polytope corresponding to the D5 Lie algebra by The McKay Correspondence is a set of 3 points that can be thought of as being placed on the 1-dimensional equator of a 2-dimensional sphere S2.
* / \ *---*
There are 2 ways to choose the North pole of the 2-sphere S2
and
there are 2 ways (left-handed or right-handed)
to rotate the 2-sphere S2.
Therefore the set of 2 points on the S2 equator
represents the Binary Dihedral group {3,2,2} of order 4x3 = 12,
represented by half of the 24 vertices of a 24-cell
(for example,
take the 12 vertices of the green cuboctahedron

at the central time = zero spacelike slice of the 24-cell).
Note that the cuboctahedron is the Root Vector Diagram of the 12+3=15-dimensional D3 Lie algebra.
It has N = 40 root vectors, so its Coxeter number H is H = N / n = 40 / 5 = 8.
The excess number of root vectors for each of the 5 copies of A1=B1=C1 is 8 - 2 = 6.
The extended affine Coxeter-Dynkin diagram is
1 1 \ / 2---2 / \ 1 1
so that the sum of the nodes (degrees of irreducible representations of {3,2,2}) is the Coxeter number 8 and the sum of the squares of the nodes (order of {3,2,2}) is 12.
J. M. Landsberg has an Algebraic Geometry point of view of D5.
the 6-dimensional polytope formed by the root vectors of the Lie algebra E6 has 72 vertices. A 2-dimensional projection, by Peter McMullen, has 72 vertices in sets of 12 on 4 concentric circles, 2 of which (white centers) are double (one vertex behind another).
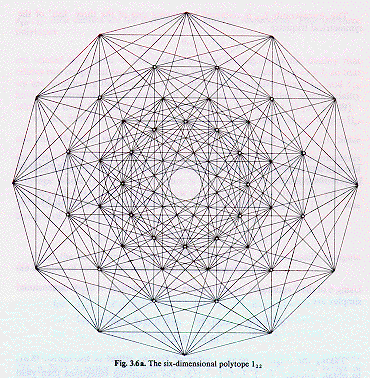
The 72-vertex Root Vector Diagram of E6 can be constructed from the 40-vertex Root Vector Diagram of D5 by, instead of adding to it hyperoctahedra cross polytopes, adding to it
a 16-vertex 5-dim hemi-hypercube (half of the 2^5 = 32 vertices of a 5-dim hypercube) above in the 6th dimension, and
a 16-vertex 5-dim hemi-hypercube (the other half of the 2^5 = 32 vertices of a 5-dim hypercube) below in the 6th dimension.
E6 has Weyl group of order 72 x 6! = 51,840 With respect to the A-D-E chain of the D4-D5-E6-E7-E8 VoDou Physics model, 78-dimensional E6 has the 28-dimensional structure of D4 = Spin(0,8) plus U(1) and 8-complex dimensional Spin(0,10) / (Spin(0,8) x U(1)) plus U(1) and 16-complex dimensional E6 / (Spin(0,10) x U(1)) With respect to the A-D-E chain of the D4-D5-E6-E7-E8 VoDou Physics model, the 16-real-dimensional Shilov boundary related to the 16-complex-dimensional E6 / (Spin(0,10) x U(1)) is physically the 8-dimensional space of Fermion Particles plus the 8-dimensional space of Fermion Antiparticles of the First Generation. Geometrically, E6 / (Spin(0,10) x U(1)) is the 78-45-1 = 32-real-dimensional complexified Octonion projective plane (CxO)P2. Note that the real Octonion projective plane is the 52-36 = 16-real-dimensional space F4/B4 = F4/Spin(9). E6 also produces the 26-real-dimensional symmetric space E6/F4 that corresponds to the complex part of the 8-dim spacetime and first-generation fermion parts of the D4-D5-E6-E7-E8 VoDou Physics model which complex part represents the Possible Worlds of the Many-Worlds.
(In CxO, x denotes tensor product. For details, see Einstein Manifolds, by Arthur L. Besse, Springer-Verlag 1987.)
A Cartan matrix is:
2 0 -1 0 0 0
0 2 0 -1 0 0
-1 0 2 -1 0 0
0 -1 -1 2 -1 0
0 0 0 -1 2 -1
0 0 0 0 -1 2
The Coxeter-Dynkin diagram is
* | *-*-*-*-*
The polytope corresponding to the E6 Lie algebra by The McKay Correspondence is not formed, as is the D6 polytope, by a set of 4 points placed on the 1-dimensional equator of a 2-dimensional sphere S2.
*--* | | *--*
representing the 16-element Binary Dihedral group {4,2,2},
but
is the 3-dimensional tetrahedron, which also has 4 vertices,
and can be formed from the square by
putting one of the 4 vertices * at a pole of the 2-sphere S2
_* _/ /| / / | *--* | \_ \ | \_\| *
The 4-vertex tetrahedron is 3-dimensional,
and
since there is no 4+3=7-dimensional simple compact Lie algebra,
the tetrahedron does not form a Lie algebra Root Vector Diagram,
but
corresponds to the order 24 Binary Tetrahedral group {3,3,2},
which is the group of quaternions
{+/-1, +/-i, +/-j, +/-k} and {(1/2)(+/-1 +/-i +/-j +/-k)}
that are the vertices of a 24-cell.

However, compare the 7-dimensional 7-sphere that is parallelizable and that expands into the 28-dimensional D4 Lie algebra that has as Root Vector Diagram the 24-cell and taha has octonionic structure.
It has N = 72 root vectors, so its Coxeter number H is H = N / n = 72 / 6 = 12.
The excess number of root vectors for each of the 6 copies of A1=B1=C1 is 12 - 2 = 10.
The extended affine Coxeter-Dynkin diagram is
1 | 2 | 1-2-3-2-1
They are the periods of products so that the sum of the nodes (degrees of irreducible representations of {3,3,2}) is the Coxeter number 12 and the sum of the squares of the nodes (order of {3,3,2}) is 24.
J. M. Landsberg has an Algebraic Geometry point of view of E6.
the 7-dimensional polytope formed by the root vectors of the Lie algebra E7 has 126 vertices.
The 126-vertex Root Vector Diagram of E7 can be constructed from the 72-vertex Root Vector Diagram of E6 by adding to it
a 27-vertex 6-dim configuration above in the 7th dimension, and
a 27-vertex 6-dim configuration below in the 7th dimension.
A 2-dimensional projection of the 6-dim 27-vertex configuration, by Peter McMullen, has 24 vertices in 2 concentric 12-gons with 3 vertices coinciding in the center. It is the real version of the Hessian complex polytope.
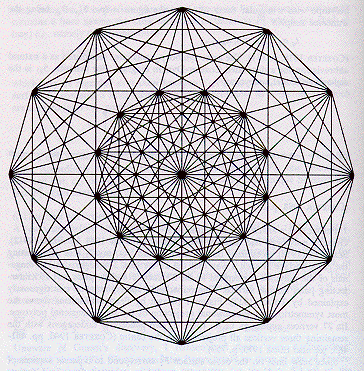
E7 has Weyl group of order 64 x 9 x 7! = 2,903,040 With respect to the A-D-E chain of the D4-D5-E6-E7-E8 VoDou Physics model, 133-dimensional E7 has the 28-dimensional structure of D4 = Spin(0,8) plus U(1) and 8-complex dimensional Spin(0,10) / (Spin(0,8) x U(1)) plus U(1) and 16-complex dimensional E6 / (Spin(0,10) x U(1)) plus U(1) and 27-complex dimensional E7 / (E6 x U(1)) With respect to the A-D-E chain of the D4-D5-E6-E7-E8 VoDou Physics model, the 27-real-dimensional Shilov boundary S1xE6/F4 related to the the 27-complex dimensional E7 / (E6 x U(1)) corresponds physically to the MacroSpace of the ManyWorlds. Geometrically, E7 / (E6 x U(1)) is the 133-78-1 = 54-real-dimensional set of complexified Octonion projective planes (CxO)P2 that are in the quaternionified Octonion projective plane (QxO)P2. Note that the quaternionified Octonion projective plane is the 133-66-3 = 64-real dimensional space E7 / (Spin(0,12)xSU(2)).
(In QxO, x denotes tensor product. For details, see Einstein Manifolds, by Arthur L. Besse, Springer-Verlag 1987.)
A Cartan matrix is:
2 0 -1 0 0 0 0
0 2 0 -1 0 0 0
-1 0 2 -1 0 0 0
0 -1 -1 2 -1 0 0
0 0 0 -1 2 -1 0
0 0 0 0 -1 2 -1
0 0 0 0 0 -1 2
The Coxeter-Dynkin diagram is
* | *-*-*-*-*-*
The polytope corresponding to the E7 Lie algebra by The McKay Correspondence is the 6-vertex octahedron, each vertex of which is the midpoint of an edge of the E6 McKay Polytope, the 6-edge tetrahedron
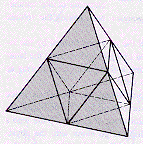
The 6-vertex octahedron is 3-dimensional,
and
since there is no 6+3=9-dimensional simple compact Lie algebra,
the octahedron does not form a Lie algebra Root Vector Diagram,
but
corresponds to the order 48 Binary Octahedral group {4,3,2}
which is the group of quaternions
{+/-1, +/-i, +/-j, +/-k} and {(1/2)(+/-1 +/-i +/-j +/-k)}
and {(1/(sqrt(2))(+/-X +/-Y)}
(where X and Y are distinct elements of {1,i,j,k})
that are the 48 vertices of a 24-cell and a dual 24-cell,
since the 24-cell is self-dual with 24 vertices, 96 edges,
96 triangular 2-dim faces, and 24 octahedral 3-dim faces.
It has N = 126 root vectors, so its Coxeter number H is H = N / n = 126 / 7 = 18.
The excess number of root vectors for each of the 7 copies of A1=B1=C1 is 18 - 2 = 16.
The extended affine Coxeter-Dynkin diagram is
2 | 1-2-3-4-3-2-1
They are the periods of products so that the sum of the nodes (degrees of irreducible representations of {4,3,2}) is the Coxeter number 18 and the sum of the squares of the nodes (order of {4,3,2}) is 48.
J. M. Landsberg has an Algebraic Geometry point of view of E7.
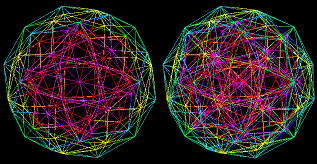
the 9-dimensional polytope formed by the root vectors of the Lie algebra E8 has 240 vertices (it is the Witting polytope). A 2-dimensional projection of the 120+120 = 240 vertices looks like this:

The 240-vertex Root Vector Diagram of E8 can be constructed from the 126-vertex Root Vector Diagram of E7 by adding to it
a 56-vertex 7-dim configuration plus 1 polar vertex above in the 8th dimension, and
a 56-vertex 7-dim configuration plus 1 polar vertex below in the 8th dimension.
A 2-dimensional projection of the 7-dim 56-vertex configuration, by Peter McMullen, has 54 vertices in 3 concentric 18-gons with 1 pair of opposite vertices coinciding in the center. It can also be represented as 56 vertices in 4 concentric 14-gons, related to its 56 vertices being the compound of 7 3-dim cubes, for 7x8 = 56 vertices.

E8 has Weyl group of order 128 x 27 x 5 x 8! = 696,729,600 With respect to the A-D-E chain of the D4-D5-E6-E7-E8 VoDou Physics model, 248-dimensional E8 has the 28-dimensional structure of D4 = Spin(0,8) plus U(1) and 8-complex dimensional Spin(0,10) / (Spin(0,8) x U(1)) plus U(1) and 16-complex dimensional E6 / (Spin(0,10) x U(1)) plus U(1) and 27-complex dimensional E7 / (E6 x U(1)) plus SU(2) and 28-quaternion dimensional E8 / (E7 x SU(2)) With respect to the A-D-E chain of the D4-D5-E6-E7-E8 VoDou Physics model, the 28-quaternion dimensional E8 / (E7 x SU(2)) might correspond physically to a Correlated MacroSpace, each point of which is a Correlated set of ManyWorlds. The Correlated MacroSpace is to MacroSpace as the space of Lie Sphere Correlations is to SpaceTime, and as Correlation Structure is to Nearest Neighbor Structure. From another (possibly equivalent) physical viewpoint, E8 / (E7 x SU(2)) might correspond to the F-theory of Spacelike Branes. From yet another (possibly equivalent) physical viewpoint, E8 might correspond to the global symmetry group of the D4-D5-E6-E7-E8 VoDou Physics model considered as being a real hyperfinite II1 von Neumann algebra factor. Geometrically, E8 / (E7 x SU(2)) is the 248-133-3 = 112-real-dimensional set of quaternionified Octonion projective planes (QxO)P2 that are in the octonionified Octonion projective plane (OxO)P2, which is the 248-120 = 128-real dimensional space E8 / Spin(0,16).
(In OxO, x denotes tensor product. For details of the geometry of (OxO)P2, see Einstein Manifolds, by Arthur L. Besse (Springer-Verlag 1987) and Geometry of Lie Groups, by Boris Rosenfeld (Kluwer 1997).)
E8 is closely related to the Clifford Algebra Cl(8).
A Cartan matrix is:
2 0 -1 0 0 0 0 0
0 2 0 -1 0 0 0 0
-1 0 2 -1 0 0 0 0
0 -1 -1 2 -1 0 0 0
0 0 0 -1 2 -1 0 0
0 0 0 0 -1 2 -1 0
0 0 0 0 0 -1 2 -1
0 0 0 0 0 0 -1 2
The Coxeter-Dynkin diagram is
* | *-*-*-*-*-*-*
The polytope corresponding to the E8 Lie algebra by The McKay Correspondence is the 12-vertex icosahedron, each vertex of which is at a Golden Ratio point of an edge of the E7 McKay Polytope, the 12-edge octahedron
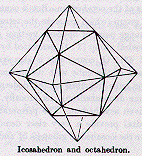
The 12-vertex octahedron is 3-dimensional,
but its 12 vertices in 3 dimensions
do not form a Lie algebra Root Vector Diagram,
but
corresponds to the order 120 Binary Icosahedral group {5,3,2},
which is the group of quaternions
that are the 120 vertices of a 600-cell,
which can be formed by
24 vertices of a 24-cell plus 96 vertices at Golden Ratio
points on the 96 edges of the 24-cell.
Note that if the 12 vertices had been put at the midpoints of the 12 edges of the octahedron, the resulting polytope would have been a cuboctahedron,
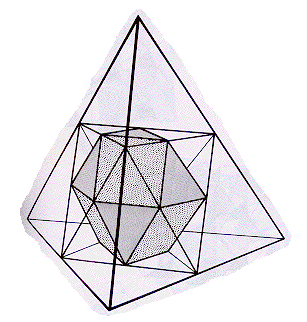
which is not a McKay Polytope, but does have 12 vertices in 3 dimensions that do form the Root Vector Diagram of the 12+3=15-dimensional D3 Lie algebra.
E8 has N = 240 root vectors, so its Coxeter number H is H = N / n = 240 / 8 = 30.
The excess number of root vectors for each of the 8 copies of A1=B1=C1 is 30 - 2 = 28,
which is consistent with picturing E8 as being made of 8 copies of the 3-sphere S3 Lie algebra plus 8 copies of the Spin(8) Lie algebra that is an expanded version of the 7-sphere S7 Malcev algebra.
The extended affine Coxeter-Dynkin diagram is
3 | 1-2-3-4-5-6-4-2
They are the periods of products so that the sum of the nodes (degrees of irreducible representations of {5,3,2}) is the Coxeter number 30 and the sum of the squares of the nodes (order of {5,3,2}) is 120.
If you form, by including reflections, the Double of the E8 McKay Group, that is, the Double of the 120-dimensional Binary Icosahedral Group, you get the 240-dimensional Double Binary Icosahedral Group, the elements of which are in 1-1 correspondence with
Note that the 48-element Double Binary Tetrahedral Group and the 96-element Double Binary Octahedral Group are not in 1-1 correspondence with the 72 root vectors of E6 and the 126 root vectors of E7.
J. M. Landsberg has an Algebraic Geometry point of view of E8.
The AN Lie algebra is SU(N+1), which is a subalgebra of U(N+1) with U(N+1) / SU(N+1) = U(1).
AN is based on the 2^(N+1)-dimensional graded extrerior (wedge) algebra of an (N+1)-dimensional vector space, each grade of degree k forming a ( (N+1) k )-dimensional representation of SU(N). The adjoint representation of U(N+1) is formed by the tensor product of the vector and pseudo-vector (degrees 1 and N) representations.
The Weyl group of SU(N) is the permutation group S_N with N! elements.
The Center of SU(N) is Z_N with N elements.
As N approaches infinity, the Center of SU(N) approaches Z,
the discrete subgroup of the Unit Circle U(1) defined by the Nth roots of unity approaches the continuous group U(1), and
a Symplectic Phase Space with signature (+,-) of Canonical Variables p and q
can be defined as described in hep-th/9901104 by Hitoshi Nishino, who says "... In ... [the large N limit] ... of an U(N) ... theory, the commutators for NxN matrices Z and W are replaced by the Poisson bracket
where p and q are commuting variables in the large N limit, which were originally non-commuting variables, satisfying [ q , p ] = 2 PI i / N. ... We first review the parametrization of U(N) NxN matrices in terms of canonical variables p and q and its effect on the commutators in the large N limit. Any NxN complex matrix Z can be expanded in terms of two unitary NxN matrices U and V , satisfying
U = e^(i p) ; V = e^(i q) ; [ q; p ] = 2 PI i / N
with so-called canonical variables p and q, as
= SUM(m,n = 0, N-1) z_mn e^(i m p) e^(i n q)
z_mn = 1 / N tr (U^m Z V^n )
... the eigenvalues of p and q can be chosen to be
In the large N limit, p and q become mutually commuting c-numbers ... . Moreover, the eigenvalues of p and q become continuous taking all the real values in - PI < p < PI , - PI < q < PI, behaving like a pair of coordinates for a phase space. In such a limit, the Z ... becomes just an ordinary Fourier expansion in terms of p and q, which we call z(p,q):
z_mn = INT(-PI, PI) dp/2PI INT(-PI, PI) dq/2PI z(p,q) e^(i m p) e^(i n q)
Accordingly, we have
[ Z , W ] approaches ( 2 PI / N ) ( (d_p Z)(d_q W) - d_q Z)(d_p W) )
... [so that] an U(N) commutator can become a Poisson bracket in the large N limit. Note that due to the symplectic feature of these two coordinates, it is natural to have the indefinite signature (+,-) in the (p,q) space, and it is convenient to use the coordinates
... "
The ( p, q ) space may be related to (1+1)-dimensional Quantum Field Theory and to the Conformal Group in 2 real dimensions, which has an infinite number of generators.
All modular invariant partition functions for the Conformal Field Theories associated to the affine A1 algebra have been classified by Cappelli, Itzykson and Zuber, who found they fall into an A-D-E pattern. Terry Gannon, in math.QA/9902064, gives a proof of their result that is an order of magnitude simpler and shorter. His further comments include:
Yang-Hui He and Jun S. Song, in hep-th/9903056, review many types of A-D-E Correspondences, saying in their abstract:
"The ubiquitous A-D-E classification has induced many proposals of often mysterious correspondences both in mathematics and physics. The mathematics side includes quiver theory and the McKay Correspondence which relates finite group representation theory to Lie algebras as well as crepant resolutions of Gorenstein singularities. On the physics side, we have the graph-theoretic classification of the modular invariants of WZW models, as well as the relation between the string theory nonlinear sigma-models and Landau-Ginzburg orbifolds. We here propose a unification scheme which naturally incorporates all these correspondences of the A-D-E type in two complex dimensions. An intricate web of inter-relations is constructed, providing a possible guideline to establish new directions of research or alternate pathways to the standing problems in higher dimensions."
The 2-dimensional Conformal Group contains some global transformations that cannot be continuously deformed to the identity, such as the modular group PSL(2,Z) = SL(2,Z) / Z_2 which is defined by transforming T into ( aT + b ) / ( cT + d ) for integers a,b,c,d and ad - bc =1.
When you take into account Constraint Equations of (1+1)-dimensional Quantum Field Theory, according you get the 26-dim Bosonic Unoriented Closed String Theory that is useful in describing the Structure of MacroSpace. The Bosonic Unoriented Closed String Theory in 26-dimensional Space has:
a first excited level with massless particles, including a Spin 2 Graviton, and
a Scalar Dilaton.
The 26-dimensional space of signature (1,25) of the Unoriented Closed Bosonic String Theory corresponds to the Lorentz Leech Lattice.
The DN Lie algebra Spin(2N) is defined by the 2^(2N)-dimensional Clifford Algebra Cl(2N), being the commutator algebra of the ( 2N ( 2N-1 ) / 2 )-dimensional bivector grade-2 part of Cl(2N). DN generates the Lie Group Spin(2N), which is the double-cover of the group of rotations in the 2N-dimensional vector grade-1 part of Cl(2N).
The Weyl group of Spin(2N) is product of (N-1) copies of Z_2 and the permutation group S_N with N! elements, with a total of 2^(N-1) N! elements.
Why is the vector space of Cl(2N) of dimension 2N, while the Weyl Goup Reflection Space has only N dimensions? Consider the N axes of the Weyl Goup Reflection Space, and take the positive and negative direction basis vector of each axis to be independent, thus getting 2N independent basis vectors to form the 2N-dimenisonal vector space of Cl(2N).
The Clifford Algebra Cl(2N) has dimensionality equal to the number of subsets of a set of 2N elements,. The Weyl group of DN has dimensionality equal to the number of permutations of a set of N elements, times the number of subsets of (N-1) elements.
Note that:
The Periodicity-8 Cycle of real Clifford Algebras ends at the Spin(8) D4 Clifford Algebra Cl(8).
What about the odd dimensions, which form the BN series of Lie algebras?
- The Spin(7) B3 Clifford Algebra Cl(7) has 128 elements which is more than the 2^3 3! = 48 elements in the Weyl group of B4. The Spin(7) 7-dimensional vectors have the same dimensionality as a natural 7-dimensional subspace of the 8-dimensional Spin(7) spinors.
- The Spin(9) B4 Clifford Algebra Cl(9) has 512 elements which is more than the 2^4 4! = 384 elements in the Weyl group of B4. The Spin(9) 9-dimensional vectors have dimensionality 9 which is LESS THAN the dimensionality of the 16-dimensional Spin(9) spinors.
- The Spin(11) B5 Clifford Algebra Cl(9) has 2,048 elements which is LESS THAN the 2^5 5! = 3,840 elements in the Weyl group of B4. The Spin(11) 11-dimensional vectors have dimensionality 11 which is LESS THAN the dimensionality of the 32-dimensional Spin(11) spinors.
As noted by Daniel Browning:
Further, note that the Spin(8) D4 Lie algebra and the Spin(9) B4 Lie algebra are both of rank 4, and that the exceptional Lie algebra of rank 4 is F4, which is 52-dimensional and can be seen as being made up of the sum of 36-dimensional Spin(9) B4 plus its 16-dimensional spinors, and that the Weyl group of F4 has 2^7 3^2 = 1,152 elements, so that the number of elements of Cl(9) is LESS THAN the 1,152 elements of the Weyl group of F4, so if you use F4 (bivectors plus spinors) instead of B4 (bivectors only), then the Clifford element number / Weyl group order property transition takes place before Cl(9), which is coincident with Periodicity-8 Cycle of real Clifford Algebras.
Let x denote the real tensor product and M(R,16) denote the 16x16 real matrix algebra.
We have the periodicity property Cl(2N+8) = Cl() x M(R,16) = Cl(2N) x Cl(8) so that
and therefore
If the signature of the Clifford Algebra vector space is important, it can be taken into account, since
Cl(N+8,N) = Cl(N,N) x Cl(8,0) = Cl(N,N) x M(R,16) = Cl(N,N+8)
Cl(N-4,N+4) = Cl(N,N).
Click on the line below for
Tony Smith's Home Page ......