In 1939, J. Robert Oppenheimer and Hartland Snyder "... studied the collapse of a spherically symmetric pressureless star of uniform density, and noted that the star's implosion, as seen by a stationary observer who remains outside, would slow and ultimately freeze as the star's surface approached the critical Schwarzschild radius. Yet they also clearly explained that no such freezing of the implosion would be seen by observers riding in with the collapsing matter - these observers would cross inside the critical circumference in a finite proper time, and thereafter would be unable to send a light signal to observers on the outside. This extreme difference between the descriptions in the two reference frames proved exceptionally difficult to grasp. The two descriptions were not clearly reconciled until
[see Past-Future Asymmetry of the Gravitational Field of a Point Particle (Phys. Rev. 112 (May 15, 1958) 965-967) - (279k pdf file)] ... once the star fell through its critical circumference, its
In 1958, "... In Moscow, Landau ... while believing Oppenheimer and Snyder's calculations, had severe trouble reconciling these two viewpoints ... [until he] read the article [in Phys. Rev. by David Finkelstein]. It was a revelation. Suddenly everything was clear. Finkelstein ... lectured at Kings College in London. Roger Penrose ... [heard] Finkelstein's lecture, and returned to Cambridge enthusiastic. In Princeton, Wheeler was intrigued at first, but was not fully convinced. ... He would become convinced only gradually, over the next several years. ...".
First above quoted material edited from the foreword of John Preskill and Kip S. Thorne to the Feynman Lectures on Gravitation, edited by Brian Hatfield (Addison-Wesley 1995)). Second above quoted material from Thorne, Black Holes and Time Warps (Norton 1994). Lev Landau (1908-1968) won the 1962 Nobel Prize in Physics.
In his 1958 paper, David Finkelstein states:
In units such that the Schwarzschild radius and the speed of light are unity, David Finkelstein's line element is:
where r = (xi xi)^(1/2) and dr = r^(-1) xi dxi.
For r greater than 1, David Finkelstein transforms by X0 = x0 + ln( r - 1 ) and Xi = xi to get the Schwarzchld line element
Note that for a number P exp(i W) that is not a positive real number, its logarithm is a Complex Number,
such as ln(P exp(i W) = ln(P) + i W or ln (-1) = ln (exp i pi) = i pi
so that for r less than 1, the transformation X0 = x0 + ln( r - 1 ) produces a Complex Number
consistent with Complex SpaceTime inside a Compton Radius Vortex.
In the D4-D5-E6-E7 physics model, Complex SpaceTime is based on the Symmetric Space
Spin(4,2) / Spin(3,1)xU(1)
where Spin(4,2) = SU(2,2) is the 15-Real-dimensional conformal group.The Symmetric Space has real dimension 15 - 6 - 1 = 8. It has local Spin(3,1) Lorentz symmetry, for special relativity. It has a local U(1) symmetry, so it is a 4-Complex-dimensional Hermitian Symmetric Space that is the physical SpaceTime inside a Compton Radius Vortex.
What about the Real SpaceTime outside the Compton Vortex? It is a Shilov Boundary.
The Type IV Hermitian Symmetric Space has a corresponding compact version that is isomorphic to a Bounded Complex Homogeneous Domain, the Shilov Boundary of which is RP1 x S3 (topologically, S1 x S3). If you let the S1 correspond to time and the S3 to space, the Shilov Boundary is the 4-Real-dimensional SpaceTime outside a Compton Radius Vortex.
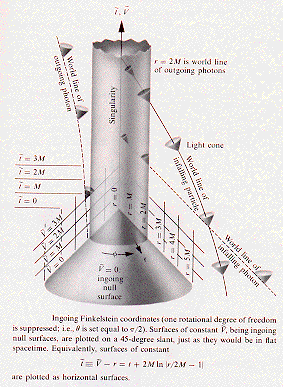
The following edited illustration from Gravitation, by Misner, Thorne, and Wheeler (Freeman 1973) shows David Finkelstein's coordinates based on photons going into the Black Hole. Their book uses units such that the Schwarzschild radius is 2M and the speed of light is unity, so that the Schwarzschild line element is

Note in particular that, after the Black Hole forms, its Event Horizon (the cylinder r = 2M) is made up of the world lines of photons and other light-cone particles that are going out from the Black Hole. Since gravitons, like photons, are massless light-cone particles, the Event Horizon can be considered to be constructed from gravitons that go out from the Black Hole, but cannot escape beyond the Event Horizon.
A Black Hole of the mass of the Sun would have a radius (proportional to its mass) of about 10^5 cm, or 1 km.
In the D4-D5-E6 model, physical spin-2 gravitons are made from Conformal Group (with de Sitter subgroup) gravitons by the MacDowell-Mansouri mechanism.
Since outside observers cannot interact directly with gravitons from the Black Hole itself, but can interact with the Event Horizon, the Event Horizon acts as a intermediary to answer the question, asked of me by Paul A. J. Wagg: If gravity is the exchange of gravitons, and gravitons from the Black Hole cannot get outside the Event Horizon to an outside observer, how can an outside observer be attracted by gravity to the Black Hole?
The Entropy of a Black Hole, and hence its Area, can also be identified with the amount of Information it carries. Jack Sarfatti, in discussing Wheeler's book Geons, Black Holes and Quantum Foam (W. W. Norton 1998), says:
"... Wheeler points out that Bekenstein showed that this Planck area of 10^-66 cm^2 [of a Planck Mass Black Hole] corresponds exactly to one c-bit of classical Shannon on the surface (event horizon) of a classical black hole. Note that a classical c-bit is not the same as a quantum q-bit of information. Wheeler also discusses Christodoulou's marvelously simple profound new application of the ancient Pythagorean theorem: "If two balls of putty collide and stick together, the mass of the new, larger ball is the sum of the masses of the balls that collided. Not so for black holes. If two spinless, uncharged black holes collide and coalesce - and if they get rid of as much energy as they possibly can in the form of gravitational waves as they combine - the square of the mass of the new, heavier black hole is the sum of the squares of the combining masses. That means that a right triangle with sides scaled to measure the masses of two black holes has a hypotenuse that measures the mass of the single black hole they form when they join. Try to picture the incredible tumult of two black holes locked in each other's embrace, each swallowing the other, both churning space and time with gravitational radiation. Then marvel that the simple rule of Pythagoras imposes its order on this ultimate cosmic maelstrom." p.p. 300-301 ... However, oddly enough, Wheeler does not, it appears, make the obvious, to me at least, connection between Christodoulo's Pythagorean theorem and Bekenstein's black hole information theory that the black hole horizon's surface area is proportional to the c-bits it has swallowed up. Wheeler's discussion of Bekenstein is later on p. 314. Clearly, Christodoulo's theorem simply means that the information of each black hole add linearly when they fuse together and attain dynamical equilibrium. ..."
The Pythagorean Property of the Mass of a Black Hole formed by merger of two Black Holes supports the Compton Radius Vortex picture of Gaja/Ganesha Physical Elementary Particles in that it is consistent with the many Mass-squared, Charge-squared, and Square-Root of the Sum of Mass-squared properties of Particle Masses and Force Strengths in Particle Physics, such as:
The Higgs scalar particle H can be considered to be a merger of 3 Compton Radius Kerr-Newman Black Holes corresponding to W+, W-, and Z0. What about Higgs mass? Then the mass mH = sqrt( mW+^2 + mW-^2 + mZ0^2 ) = sqrt( 80^2 + 80^2 + 90^2 ) = sqrt( 20,900 ) = 145 GeV. Although the Higgs H has not yet been observed, mH = 145 GeV is consistent with indirect Standard Model limits.
What about Higgs spin? The Higgs H is a scalar with spin = 0. Each of the Weak Bosons W+, W-, and Z0 is a vector with spin = 1. Look at the process of merger of the 3 Compton Radius Kerr Black Holes corresponding to W+, W-, and Z0. Since it is a 3-body merger, and I don't know a reference for 3-body Black Hole mergers, I will approximate it by using the textbook treatment of a 2-body merger of W+ and W- with the Z0 being added in a way that I guess (but have not yet fully calculated) is correct. When the W= and W- merge, their spins should be antiparallel because of a gravitational spin-spin force which is attractive for antiparallel spins (see Wald, General Relativity (Chicago 1984) page 338, problem 12.4). Since angular momentum cannot be radiated away in an axisymmetric spacetime, the resulting angular momentum from the W+ and W- should be +1 -1 = 0. What about the Z0? The Z0 violated axisymmetric symmetry, so its angular momentum should be radiated away by gravitational radiation. Therefore the final spin state of the Black Hole merged from W+, W-, and Z0 should be spin = 0, a scalar, consistent with its identification with the Higgs scalar.
Some other Particle Physics Phenomena supported by the Pythagorean Property are:
In contrast, Quantum Many Worlds Sum-Over Histories phenomena are not square-root-of sum-of-squares Black Hole merger phenomena, but are linearly additive. Examples include:
If the Event Horizon of a Black Hole has Entropy, it should also have Temperature. The temperature of a Black Hole increases as it evaporates, with a temperature that is inversely proportional to its mass, and, equivalently, inversely proportional to its radius. A Black Hole of the mass of the Sun would have a temperature of 10^(-6) degrees K.
If a Black Hole has Temperature, it should emit Radiation with a spectrum corresponding to that Temperature. If a Black Hole has greater than the stable minimum Planck mass, it will decay with a lifetime that is proportional to the cube of its mass. For a Black Hole to survive about 20 billion years, it must have a mass of at least 2 x 10^14 grams. For comparison, the Earth has mass of 6 x 10^27 grams and the Sun has a mass of 2 x 10^33 grams.
In his book Black Holes and Time Warps (Norton 1994) Kip Thorne says, on pages 428-430 and 432-433:
"... in June 1971 ... Zeldovich announced ... A spinning black hole must radiate ... a spinning metal sphere emits electromagnetic radiation ... The radiation is so weak ... that nobody has ever observed it, nor predicted it before. However, it must occur. The metal sphere will radiate when electromagnetic vacuum fluctuations tickle it. ... Zeldovich's mechanism by which vacuum fluctuations cause a spinning body to radiate. ... His sketch ...... showed a wave flowing toward a spinning object, skimming around its surface for a while, and then flowing away. The wave might be electromagnetic and the spinning body a metal sphere ... or the wave might be gravitational and the body a black hole ... The incoming wave is not a "real" wave ... but rather a vacuum fluctuation. ... the wave's outer parts ... are in the "radiation zone" while the inner parts are in the "near zone" ... the wave's outer parts move at ... the speed of light ... its inner parts move more slowly than the body's surface is spinning ... the rapidly spinning body will ... accelerate ...[the inner parts of the incoming wave] ... The acceleration feeds some of the body's spin energy into the wave, amplifying it. The new, amplified portion of the wave is a "real wave" with positive total energy, while the original, unamplified portion remains a vacuum fluctuation with zero total energy. ... Zeldovich ... proved that a spinning metal sphere radiates in this way; his proof was based on the laws of quantum electrodynamics ...
.... In September 1975 ... Zeldovich and Starobinsky ... described how their version of the laws of quantum fields in a black hole's curved spacetime ... was really equivalent ...[to]... Hawking's ...[ theory of black hole radiation ]...[ with spacetime curvature tides having a similar effect to the spinning/dragging of the metal sphere in Zeldovich's electromagnetic model ]... They had concluded that ...[ non-spinning ]... black holes cannot evaporate because of an error in their calculations ... With the error corrected ... black holes evaporate ...".
In 1974, Stephen Hawking showed, as illustrated by this figure from his book A Brief History of Time (Bantam 1988), how the Event Horizon emits Radiation:
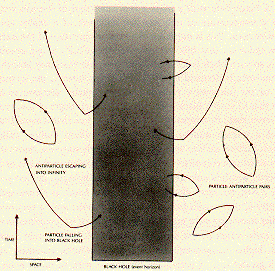
The Zeldovich-Hawking Process, in which a Virtual Pair of Musaka/Ganesha Particles near the Event Horizon can be separated with
one of the Virtual Pair going into the Black Hole
and
the other going into External Spacetime,
Cerf and Adami have written a paper "Prolegomena to a Non-Equilibrium Quantum Statistical Mechanics" in which they
"... suggest that the framework of quantum information theory ... is a reasonable starting point to study non-equilibrium quantum statistical phenomena. As an application, [they] discuss the non-equilibrium quantum thermodynamics of black hole formation and evaporation. ...For the brief transitory periods, ... the time during which a system approaches equilibrium, our bag of tricks containing the tools of statistical mechanics is of little use. The canonical phenomena of this type are relaxation or transport processes, phenomena which are usually termed "irreversible", and phase transitions for which the entropy is not a constant.
The standard approach to deal with such situations is to study the N-body dynamics of the system, with a Hamiltonian that includes an interaction term (in equilibrium statistical mechanics the Hamiltonian is a sum of non-interacting one-body terms) and the construction of equations that follow the N-particle distribution function through time: the Boltzmann equation. This approach suffers from the drawback that it can only be solved in perturbation theory, which obscures the relation to the "exact" formalism of thermodynamics. ...
[A] formalism in which the second law [of thermodynamics] is replaced by a conservation law for entropy (... in which case the second law ... [appears] as a corollary) exists in the form of the classical theory of information, introduced by Shannon. Its extension to the quantum regime is particularly interesting as it consistently describes quantum unitary dynamics which dictates that the von Neumann entropy - the quantum extension of the Shannon entropy - is a constant. ... [This] formalism ... can quantitatively describe even the approach to equilibrium and other non-equilibrium statistical phenomena. ...
The discovery of Hawking radiation appears to have plunged quantum mechanics into a deep crisis, as it seems to imply that the evaporation of black holes violates unitarity ... Hawking pointed out that the process of thermal evaporation of a black hole leads to an "information paradox". If we assume that the black hole [of mass M] is formed from a quantum mechanically pure state S = 0, the entropy of the purely thermal blackbody radiation left behind after evaporation should be of the order M^2, i.e., a pure state evolved to a mixed one. This contradicts the unitary evolution of quantum states, according to which ... the entropy of a closed system is a constant, in this particular case the constant zero. ...
... beyond the information paradox pointed out by Hawking, as observed by Zurek we also need to match the black hole entropy ... with the entropy of approximately thermal radiation ... with black hole temperature ... .
we will focus here on the most conservative explanation, namely that Hawking radiation is effectively non-thermal (in the sense that quantum correlations between the radiation and the state of the black hole exist in principle) ...
While the fields do live in a product Hilbert space, the wavefunction of an EPR pair created at the event horizon of the black hole indirectly becomes entangled with the hole the moment one of the particles crosses the horizon (even though the quantum fields are separated by space-like distances) and the combined quantum state becomes inseparable. This situation is not unlike the scenario we noted in the formation of the black hole, where the accreted particle and the radiation it emits when tumbling into the black hole can be considered an entangled, EPR-type state (albeit with real rather than virtual energy). Just as in that case the radiation ... shared no entropy with the black hole, neither does the Hawking radiation, while still being entangled with it. Thus, the Hawking radiation carries "information" about the inside of the hole in the same manner as the measurement of EPR partners separated by space-like distances reveals correlations in measurement devices that are at space-like distances.
Yet, a fundamental problem remains that is unlikely to be solved within the present formalism. The Hawking radiation - while emitted in a unitary manner and while information loss certainly does not take place - remains causally uncorrelated to the black hole as long as the horizon separates the black hole entropy from the radiation field. In a sense, we have to wait until the last moment - the disappearance of the black hole - for the entropy balance to be restored. This appears to put a severe strain on current black hole models, as it is hard to imagine that this much entropy can be stored in an ever-shrinking black hole. This problem is likely due to our incomplete understanding of late-stage black holes, rather than a problem intrinsic to quantum mechanics.
... An alternative solution would present itself if the Bekenstein-Hawking entropy could be understood in terms of a conditional entropy. In that case, entropy flow from the black hole to the outside via the formation of virtual pairs is understood easily, as the member of the pair that crosses the horizon not only has negative energy but also negative conditional entropy. As a conditional entropy can become as negative as the marginal entropy of the system it is a part of, we can circumvent the argument that "the black hole cannot store the information until the end because it runs out of quantum states", because the radiation could "borrow" as much entropy as necessary from the black hole until the horizon has disappeared. ... It is not inconceivable ... that a quantum statistical information theory extended to curved space-time would reveal ... that the Bekenstein-Hawking entropy is in fact conditional ...
... We emphasize that great care is needed in using the concepts of entropy and information consistently: information, for example, can never be "stored" in one system (e.g., a black hole). Rather, information is a measure of correlation between two systems, which implies that information is always stored in correlations. ... radiation and black hole matter are unstable at any time, and transitions must occur as long as matter of either kind is present. Yet, a consistent formulation of the correlations between radiation and matter shows that entropy is not created during the process, and consequently that information is conserved. ....".
As Kip Thorne says in his book Black Holes and Time Warps (Norton 1994, pages 491-492),
"... in 1974 ... Hawking inferred as a byproduct of his discovery of black hole evaporation ... that vacuum fluctuations near a [Black Hole]'s horizon are exotic: They have negative average energy density as seen by outgoing light beams near the hole's horizon. ... it is this exotic property of the vacuum fluctuations that permits the hole's horizon to shrink as the hole evaporates ... The horizon distorts the vacuum fluctuations away from the shapes they would have on Earth, and by this distortion it makes their average energy density negative,that is, that is, it makes the fluctuations exotic. ... Gunar Klinkhammer ... has proved that in flat spacetime ... vacuum fluctuations can never be exotic ... Robert Wald and Ulvi Yurtsever have proved that in curved spacetime ... the curvature distorts the vacuum fluctuations and thereby makes them exotic. ...".
was developed by Kerr (who generalized to add angular momentum J to mass M in 1963) and by Newman (who generalized to add charge e in 1965), according to the book General Relativity, by Robert Wald (Chicago 1984). Let a = J / M. Then the Kerr-Newman SpaceTime metric in spatially spherical coordinates t, r, T, P (where the angular momentum axis is T = 0) is
- ( 2a sin^2(T) (r^2 + a^2 - D ) / S ) dt dP +
+ ( ( ( r^2 + a^2 )^2 - D a^2 sin^2(T) ) / S ) sin^2(T) dP^2 +
+ S / D dr^2 +
+ S dT^2
and the Electromagnetic Vector Potential is
where
and
If e = M = 0 and a is nonzero, then the Kerr-Newman metric is just the metric of Minkowski space in spatially spherical coordinates, and the singularity at S = 0 is a coordinate singularity located at a Ring of radius a in the plane z = 0 in cartesian coordinates t, x, y, z, that is,
"... I'd like to point out that the linearized Einstein-Maxwell fields are actually double-valued and can be made single-valued by choosing a branch cut which spans the ring and makes it into a DISK. In fact, there is a footnote to that effect in one of Ted Newman's papers (Maxwell's equations and complex Minkowski space, J. Math. Phys. 14, 102, 1973) which he told me was in response to a comment by the anonymous referee who turned out to be Roger Penrose! A careful analysis of the EM case in flat R^4 appears in my paper http://arXiv.org/pdf/gr-qc/0108041 (Of course, you could instead go to the covering space, but people like Newman don't think that has physical significance.)PS: I've been playing with complex spacetime since 1966. For example, see my book Quantum Physics, Relativity, and Complex Spacetime (now out of print, to be updated some day). ...".
If M and a are nonzero, then there are Closed Timelike Loops in a neighborhood of the Ring.
In all 3 cases,
In astro-ph/9707165, Lasenby, Doran, Dobrowski, and Challinor say:
"... Gauge-theory gravity, expressed in the language of Geometric Algebra [Clifford Algebra],
allows very efficient numerical calculation of photon paths. ... We discuss ... applications of a gauge theory of gravity ... The theory employs [two] gauge fields in a flat Minkowski background spacetime to describe gravitational interactions. ... The first of these, h(a), is a position-dependent linear function mapping the vector argument a to vectors. The position dependence is usually left implicit. Its gauge-theoretic purpose is to ensure covariance of the equations under arbitrary local displacements of the matter fields in the background spacetime. The second gauge field, W(a), is a position-dependent linear function which maps the vector a to bivectors. Its introduction ensures covariance of the equations under local rotations of vector and tensor fields, at a point, in the background spacetime. Once this gauging has been carried out, and a suitable Lagrangian for the matter fields and gauge fields has been constructed, we find that gravity has been introduced. ... the theory is formally similar in its equations (hence local behaviour) to the Einstein-Cartan-Kibble-Sciama spin-torsion theory, but it restricts the Lagrangian type and the torsion type (... torsion that is not trivector type leads to minimally coupled Lagrangians giving non-minimally coupled equations for quantum fields with non-zero spin). ...
If we restrict attention to situations where the gravitating matter has no spin, then there are still differences between general relativity and the theory presented here. These differences arise when time reversal effects are important (e.g. horizons), when quantum effects are important, and when topological issues are addressed. ...
... within the framework of gauge-theory gravity, the Kerr singularity is composed of a ring of matter, moving at the speed of light, which surrounds a disk of pure isotropic tension. ...
... As an interesting aside, we note that self-consistent homogeneous cosmologies, based on a classical Dirac field, require that k = 0 (the universe is spatially flat). ... ".
In the paper Gravity, gauge theories and geometric algebra, downloadable from the web page of The Geometric Algebra Research Group at Cavendish Laboratory, University of Cambridge, Lasenby, Doran, and Gull say: that "...fermionic matter would be able to detect the center of the universe if k=/= 0 [if the univese were not spatially flat] ...".
In the paper Effects of Spin-Torsion in Gauge Theory Gravity, downloadable from the web page of The Geometric Algebra Research Group at Cavendish Laboratory, University of Cambridge, Doran, Lasenby, Challinor, and Gull say: that "... Within [Gauge-Theory Gravity], torsion is viewed as a physical field derived from the gravitational gauge fields. This viewpoint has some conceptual advantages over that used in differential geometry, where torsion is regarded as a property of a non-riemannian manifold. ... for a massive spinning point-particle, moving in a gravitational background with torsion ...the motion is not generally geodesic, the spin vector is not Fermi-transported, and the particle couples to the torsion. ... spinning point particles see a preferred direction in space due to the spin of the matter field. ... with spin there are extra physical fields present which have observable consequences. ...".
In gr-qc/9910099, Chris Doran says: "...
... is global and involves a time coordinate which represents the local proper time for free-falling observers on a set of simple trajectories. ... The Kerr solution ... is global, making it suitable for studying processes near the horizon. ... the time coordinate measured by a family of free-falling observers brings the Dirac equation into Hamiltonian form ... This form of the equations also permits many techniques from quantum field theory to be carried over to a gravitational backgroundwith little modification. ... ".
If e^2 + a^2 is less than M^2, then D = 0 and
and
the Inner Event Horizon is at r = r- = M - sqrt( M^2 - a^2 - e^2)
Outside the Outer Event Horizon you can escape the Black Hole, but you must rotate in the same direction as the Black Hole if you are within the Static Limit outer boundary of
the Ergosphere at r = M + sqrt( M^2 - a^2 cos^2(T) - e^2)
This effect can be said to be due to extreme frame dragging, or to timelike translations becoming spacelike as though they had been Wick rotated in Complex SpaceTime.
Ergosphere (white), Outer Event Horizon (red), Inner Event Horizon (green), and Ring Singularity (purple) from Black Holes - A Traveller's Guide, by Clifford Pickover (Wiley 1996).
In his paper "Generation and Evolution of Magnetic Fields in the Gravitomagnetic Field of a Kerr Black Hole", Ramon Khanna says: "... a rotating black hole can generate magnetic fields in an initially un-magnetized plasma. In axisymmetry a plasma battery can only generate a toroidal magnetic field, but then the coupling of the gravitomagnetic potential with toroidal magnetic fields generates poloidal magnetic fields. Even an axisymmetric self-excited dynamo is theoretically possible, i.e. Cowling's theorem does not hold close to a Kerr black hole. Due to the joint action of gravitomagnetic battery and gravitomagnetic dynamo source term, a rotating black hole will always be surrounded by poloidal and toroidal magnetic fields (probably of low field strength, though). The gravitomagnetic dynamo source may generate closed poloidal magnetic field structures around the hole, which will influence the efficiency of the Blandford-Znajek mechanism [whereby coupling of the gravitomagnetic potential with a magnetic field results in an electromotive force that drives currents that may extract rotational energy from a black hole].The "shear-of-space" driven fraction of a global current can be assessed by a kinematic simulation of a zero-angular-momentum flow. The major part of the resulting current system is generated and closed in the corona near the hole. In a realistic accretion-ejection flow, the plasma shear in the ergosphere of a rapidly rotating black hole will be similar to the shear of space. The current system should therefore have a similar structure ... which means that the energy extracted from the hole is likely to be deposited in the disk corona.
The Dyadosphere is defined by Remo Ruffini in astro-ph/9811232 as being the region, outside the horizon of a black hole with an electromagnetic field (EMBH), where the electromagnetic field exceeds the Heisenberg-Euler critical value E = m^2 c^3 / hbar e (where m and e are the electron mass and charge) for e+ e- pair production. The Dyadosphere will dissipate in about 10^7 sec, or less than a year. In a very short time on the order of hbar / m c^2 a very large number of pairs is created there and reaches thermodynamic equilibrium with a photon gas. In the ensuing enormous Pair-ElectroMagnetic pulse (PEM pulse), a large fraction of the extractable energy of the EMBH in the sense of will be carried away. The PEM-pulse will interact with some of the baryonic matter of the uncollapsed material and the associated emission is closely related to the observed properties of GRB sources. The electromagnetic field of the remnant will further dissipate in the acceleration of cosmic rays or in the propulsion of jets on much longer time scales. Up to 50% of the mass energy of an extreme EMBH, whose charge is Qmax = R c^2 / sqrt(G) (where R is the outer horizon radius), can be stored in its electromagnetic field. Even in the case of an extreme EMBH the charge to mass ratio is one quantum of charge per 10^18 nucleons. A large fraction of the energy of an EMBH can be extracted by Heisenberg-Euler electromagnetic field pair production. This energy extraction process only works for EMBH black holes whose irreducible mass is less than 10^6 solar masses. The Dyadosphere radius is maximized for the extreme case. The Dyadosphere exists for EMBH's with mass larger than the upper limit for neutron stars, about 3.2 solar masses, all the way up to a maximum mass of 6 x 10^5 solar masses. Correspondingly smaller values of the maximum mass are obtained for EMBH's with less than the maximal charge of an extreme EMBH. In the following figure, the red and blue lines are the Dyadosphere radius and Outer Event Horizon radius for an extreme EMBH, while the gold and purple lines are Dyadosphere radius and Outer Event Horizon radius for an EMBH with charge Q = 0.01 Qmax.
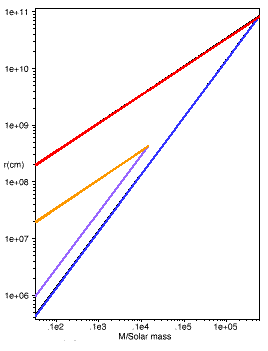
For EMBH's with mass larger than the maximum value, the electromagnetic field (whose strength decreases inversely with the mass) never becomes critical. For an EMBH of 10 solar masses, the energy of pairs near the horizon can reach 10 GeV. For an EMBH of 10^5 solar masses, the energy of pairs never goes over a few MeV. These two values of the mass are representative of objects typical of the galactic population or for the nuclei of galaxies compatible with our upper limit of the maximum mass of 6 x 10^5 solar masses. The time scale of the dyadosphere discharge is of the order of 10^19 sec. Such a time scale is much shorter than the characteristic magnetohydrodynamical time scales. We expect that the formation of the dyadosphere should only occur during the gravitational collapse itself and in the process of formation of the EMBH, with the formation of a charge depleted region with an electric field sufficient to polarize the vacuum. As Ruffini says, "... From a fundamental point of view, the process occuring in the Dyadosphere represents the first mechanism capable of extracting large amounts of energy from a Black Hole with an extremely high efficiency. ... Basic energy requirements for gamma ray bursts (GRB), including GRB971214 recently observed at z = 3.4, can be accounted for by processes occurring in the Dyadosphere.". Ruffini ( along with, in some papers, co-authors ) discusses The Dyadosphere of Black Holes and Gamma-Ray Bursts in astro-ph/9905071, astro-ph/9905072., and astro-ph/0106532.
The Maximal Extension of SpaceTime for a Black Hole with e^2 + a^2 is less than M^2 is shown in Figure 12.4 from General Relativity by Robert M. Wald (Chicago 1984):
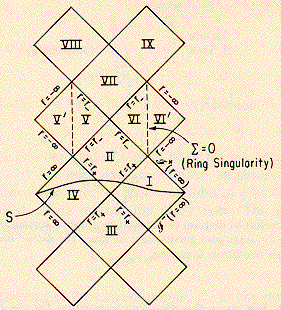
Wald says: "... Region I ... is the asymptotically flat region covered in a nonsingular fashion by the original coordinates with r greater than r+. By extending through the Coordinate Singularity at r = r+, we obtain Region II representing a Black Hole, Region III representing a White Hole, and Region IV representing another asymptotically flat region ... However, ... instead of encountering a true singularity at the Top Boundary of Region II and the Bottom Boundary of Region III, we encounter merely another Coordinate Singularity at r = r-. Thus, we can extend Region II through r = r- to obtain Regions V and VI. These regions contain the Ring Singularity at SIGMA = 0 and ... [ as in the case in which e^2 + a^2 is greater than M^2] ... one can pass through the ring singularity to obtain another asymptotically flat Region VI' with r going to negative infinity. (In this asymptotically flat Region VI' the Ring Singularity is a naked singularity of negative mass. ... ) One may then continue to extend the ... SpaceTime upward ad infinitum to obtain a Region VII, identical in structure to Region III, and obtain Regions VIII and IX, identical in structure to Regions IV and I, etc. Similarly, one may extend ... downward ad infinitum. ... Thus, an observer starting in Region I ... may cross the Event Horizon at r = r+ and enter the Black Hole Region II. ... the observer may pass through the Inner Horizon r = r- (which is a Cauchy Horizon for the hypersurface S ... ), thereby entering Region V or VI. From there, he may ... pass through the Ring Singularity to a new asymptotically flat Region V' or VI', or he may enter the White Hole Region VII and from there enter the new asymptotically flat Region VIII or IX. From there he may enter the new Black Hole associated with these asymptotic regions, and continue his journey. ..."
As Wald says, "... we would, in general, expect a complicated dynamical evolution which only settles down to a stationary geometry at late times ... Thus, we are not in a position to follow the dynamical evolution of the gravitational collapse of a body which forms a Kerr Black Hole and thereby determine the detailed SpaceTime geometry inside the Black Hole. ...", so we really don't know the answer.
Wald is pessimistic, saying: "... there is good reason to believe that in a physically realistic case ... the Cauchy Horizon r = r- ... will become a true, physical singularity ...".
Wald's pessimism is supported by Hod and Piran in gr-qc/9803004, who "... study the inner-structure of a charged black-hole which is formed from the gravitational collapse of a self-gravitating charged scalar-field ...". According to Physics News Update 386-1, Hod and Piran "... have now supported previous indications showing that these Cauchy horizons are unstable; small disturbances in the black hole instantly transform them into singularity regions. In fact, their calculations suggest that generic black holes contain two singularities that are connected to each other so that all infalling matter reaches one or the other. ..."
However, I do not agree that the results of such calculations, which due to computational difficulty deal with very simplified structures, are applicable in all physically reasonable cases. Therefore, I am optimistic that such a journey might be physically reasonable.
Also, there is
and the only singularity is the Ring Singularity at z = 0 and x^2 + y^2 = a^2, which is then a Naked Singularity in that the Kerr-Newman metrics are not strongly asymptotically predictable.
Hawking and Ellis, in The LargeScale Structure of Space-Time (Cambridge 1973), show the Maximal Extension of SpaceTime at the Black Hole Ring Singularity (whether e^2 + a^2 is greater than, equal to, or less than M^2).
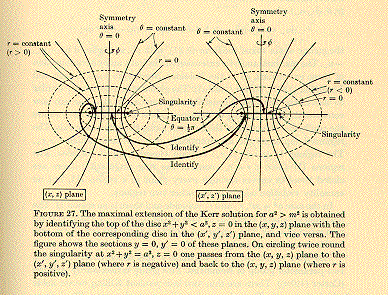
and say that:
The metric in the (x,z) SpaceTime is extended through the Ring Singularity to the (x',z') SpaceTime, with the entire maximally extended SpaceTime having coordinates (r, Theta, Phi, t) (abbreviated to (r,T,P,t). The metric in the (x,z) region has Positive r, while the metric in the (x',z') region has Negative r.At large Negative values of r, the SpaceTime is asymptotically flat but with Negative Mass.
For small Negative values of r near the Ring Singularity, the circles (r = constant, T = constant, t = constant) are Closed Timelike Curves that can be deformed to pass through any point of the extended SpaceTime.
Robert Forward, in Indistinguishable from Magic (Baen 1995), describes SpaceTime travel through the Ring Singularity. Since Closed Timelike Curves can be deformed to pass through any point of the extended SpaceTime. As Forward says, "... by making and opening [Ring Singularities] in orbit around distant stars we can travel from one star system to another by merely popping into the [Ring Singularity] in our solar system and popping out again in another [Ring Singularity] around some distant star system.
As Kip Thorne says, in Black Holes and Time Warps (Norton 1994), quoting Tom Roman, "... If ... one [can] travel over interstellar distances far faster than light, ... one can also ... travel backward in time ...", so Forward's Ring Singularity SpaceTime travel is travel in both Space and Time.
Forward also describes SpaceTime travel by SpaceTime Tunnel as proposed by Mike Morris and his teacher Kip Thorne, who call a SpaceTime Tunnel a Wormhole. As Thorne says, " ... Einstein's field equation predict[s] that ... left to [its] own devices ... [a SpaceTime Tunnel] ... opens up briefly, and then pinches off and disappears - and its total life span from creation to pinch-off is so short that nothing can travel through it, from one mouth to the other. ... the only way to hold the [SpaceTime Tunnel] open is to thread [it] with with some sort of material that pushes [its] walls apart. ... such material ... must have a Negative average energy density, as seen by a light beam travelling through it. ..."
As Don Page remarked to Morris and Thorne, Proposition 9.2.8 of the book of Hawking and Ellis shows that any SpaceTime Tunnel requires such Negative Material to hold it open.
Since Ring Singularity SpaceTime travel goes from our ordinary Positive Mass (x,z) region of SpaceTime through the Negative Mass (x'z') region and then back to our ordinary region, Ring Singularity SpaceTime travel is consistent with Morris-Thorne SpaceTime Tunnel travel with the tunnel being held open by Negative Material.
Thorne discusses other possibilities for getting Negative Material to hold open a SpaceTime Tunnel, such as ZPF vacuum fluctuations, which Hawking has shown to have Negative average energy density near the horizon of a Black Hole (thus allowing the Black Hole to decay). However, Gunnar Klinkhammer, a student of Thorne, has shown that vacuum fluctuations in flat SpaceTime can never have Negative average energy density. Such vacuum fluctuations must occur in suitably curved SpaceTime.
Therefore, I think that SpaceTime travel is most likely to be done by Ring Singularity, as was shown in the movie StarGate

that linked the StarGate to the Giza Pyramids (image from the CD-ROM Secrets of StarGate (Le Studio Canal 1994)). ( Compare a GraviPhoton 2-Torus Ring Ship. )
As Jack Sarfatti says:
Shinkai and Hayward, in gr-qc/0205041, say: "... We study numerically the stability of Morris & Thorne's first traversible wormhole, shown previously by Ellis to be a solution for a massless ghost Klein-Gordon field. Our code uses a dual-null formulation for spherically symmetric space-time integration, and the numerical range covers both universes connected by the wormhole. We observe that the wormhole is unstable against Gaussian pulses in either exotic or normal massless Klein-Gordon fields. The wormhole throat suffers a bifurcation of horizons and either explodes to form an inflationary universe or collapses to a black hole, if the total input energy is respectively negative or positive. As the perturbations become small in total energy, there is evidence for critical solutions with a certain black-hole mass or Hubble constant. The collapse time is related to the initial energy with an apparently universal critical exponent. For normal matter, such as a traveller traversing the wormhole, collapse to a black hole always results. However, carefully balanced additional ghost radiation can maintain the wormhole for a limited time. The black-hole formation from a traversible wormhole confirms the recently proposed duality between them. The inflationary case provides a mechanism for inflating, to macroscopic size, a Planck-sized wormhole formed in space-time foam. ...".
As Wald says in General Relativity (Chicago 1984),
For a spin 1 particle, with Mass m, Electric Charge Q, Magnetic Moment M, and Angular Momentum L,
so that its Gyromagnetic Ratio is 1. (see, for example, Leighton, Principles of Modern Physics, page 186, McGraw-Hill 1959).
According to pages 883 and 891-892 of Misner, Thorne, and Wheeler (Gravitation, Freeman 1973), a Kerr-Newman Black Hole Mass m, Electric Charge Q, Magnetic Moment M, and Angular Momentum L,
so that a Kerr-Newman Black Hole has Gyromagnetic Ratio 2, or, equivalently, spin 1/2.
Since the charge-to-mass ratio e / M of the Electron is about 10^21
Since the charge-to-mass ratio (in geometric units) e / M of the Proton is about 10^18
......

In 1962, David wrote (with Jauch, Schiminovich, and Speiser) the first Quaternion-SU(2) paper about Massive Charged Weak Bosons.
I learned about Clifford Algebras from studying under David Finkelstein at Georgia Tech since around 1981. Both David Finkelstein and I use the the Periodicity-8 tensor product Cl(N) = Cl(8) x ...N/8 times... x Cl(8)) in our physics models. With respect to his model, David Finkelstein says "... An assembly with Clifford statistics we call a squad. The Spinorial Chessboard shows how the dynamics, a large squad of chronons, can spontaneously break down into a Maxwellian assembly of squads of 8 chronons each. Squads of 8 are special this way. ...". Also, see, for example, the paper hep-th/0009086, Clifford Algebra as Quantum Language, by James Baugh, David Ritz Finkelstein, Andrei Galiautdinov, and Heinrich Saller, and the paper by D. Finkelstein and E. Rodriguez, The quantum pentacle, International Journal of Theoretical Physics 23, 887-894 (1984).
......