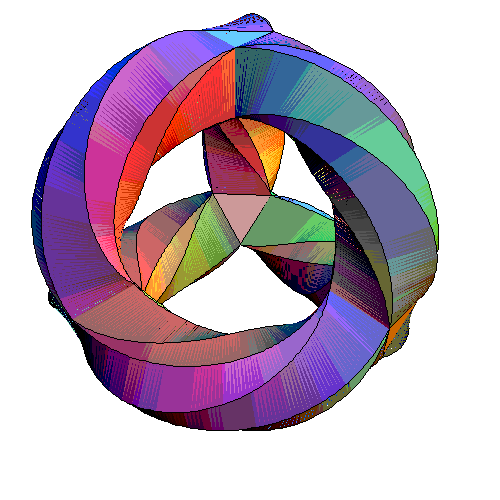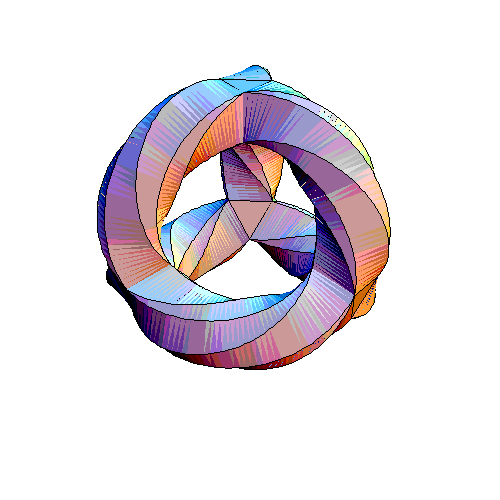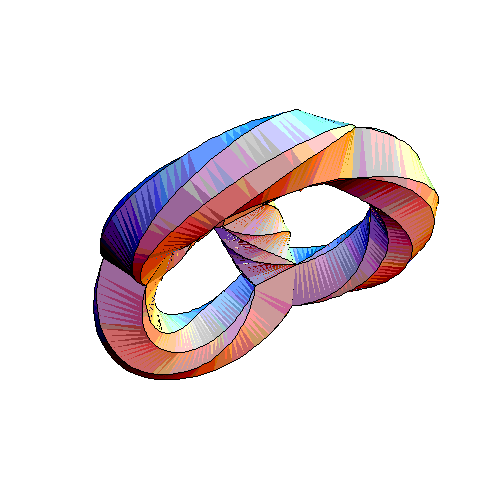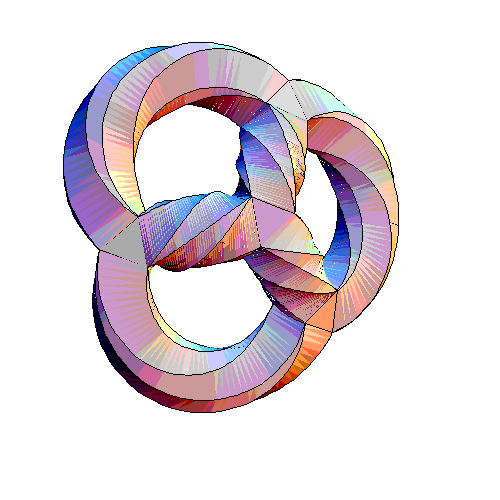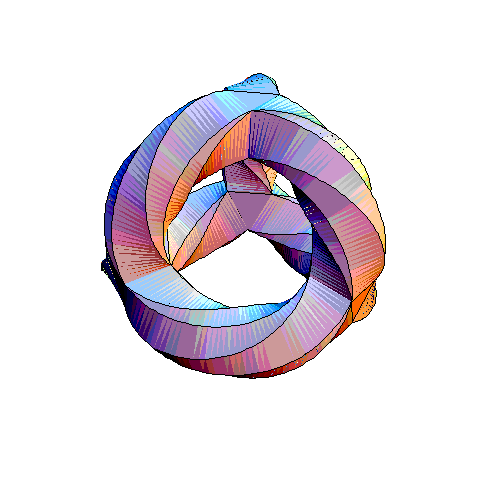In his 9 May 2005 Week
215, John Baez
says:
"... The science fiction writer Greg Egan has been
helping me understand Klein's
quartic curve ...
1) Greg Egan, Klein's quartic
curve ...
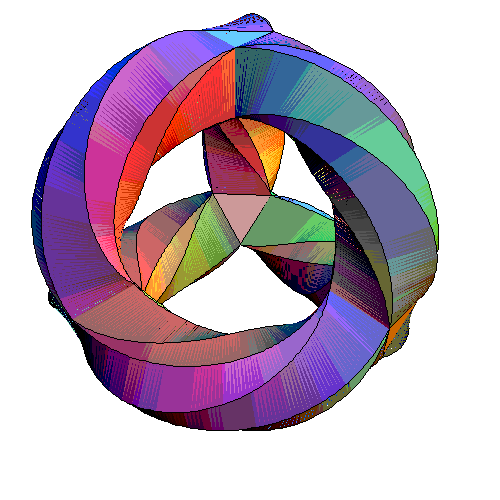
... topologically speaking, it's a 3-holed torus. It's tiled by
triangles, with 7 meeting at each vertex.
... Dual to ... a tiling of the hyperbolic plane by regular
heptagons with 3 heptagons meeting at each vertex ... is a tiling
of the hyperbolic plane by equilateral triangles with 7 triangles
meeting at each vertex.
We can take a quotient space of this by a certain symmetry
group and get a 3-holed torus tiled by 56 triangles with 7 meeting
at each vertex. This is what Egan drew!
... First, you can take any vertex and twist it, causing the 7
triangles that meet at this vertex to cycle around. ... This gives
a 7-element symmetry group.
Second, the whole thing looks like a tetrahedron, so it
inherits the rotational symmetries of a tetrahedron. This gives a
... 12-element symmetry group.
... there's also a 2-fold symmetry that corresponds to turning
the tetrahedron inside out! And Egan made a wonderful
movie of this. If a picture is worth a thousand words,
this is worth about a million ...
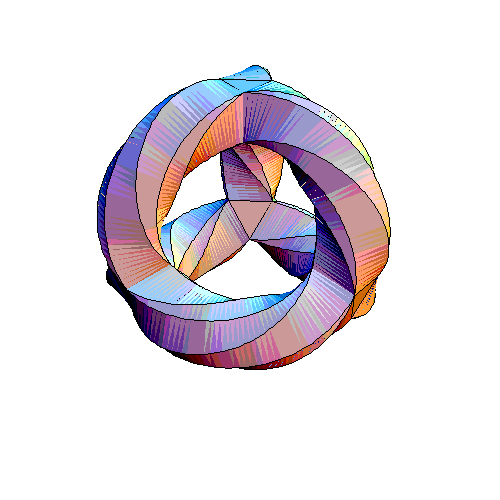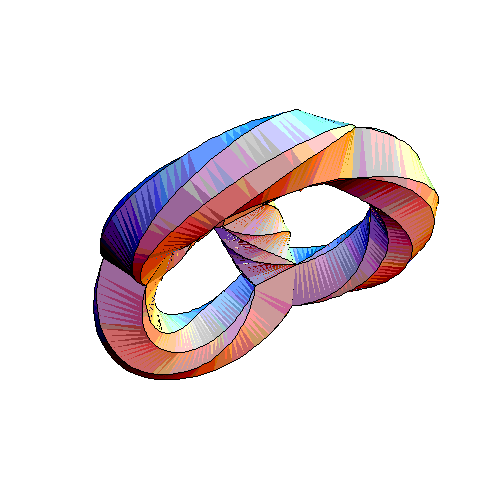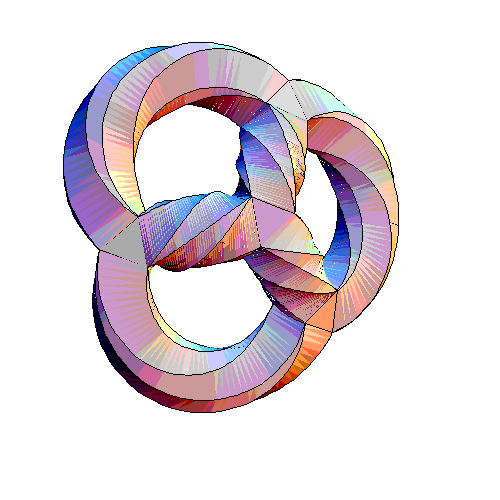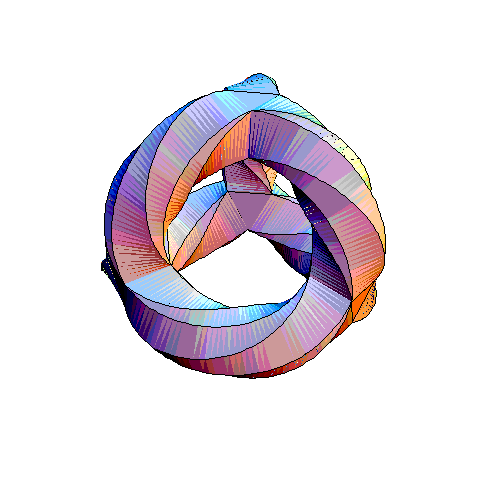
... So, we get a total of 7 x 24 = 168 symmetries.
... the tetrahedron in Egan's movie gets reflected as
it turns inside out. More precisely, if you follow the four
corners of the tetrahedron, you'll see that two come back to where
they were, while the other two get switched. So, this symmetry
acts as a reflection, or odd permutation, of the 4 corners. The
rotations act as even permutations of the corners.
This means that the Klein quartic has 24 symmetries forming a
group isomorphic to the rotation/reflection symmetry group of a
tetrahedron. ...
[ In his book Complex Regular Polytopes (2nd edition, Cambridge 1991),
Coxeter says the "... fundamental region is ... a spherical triangle
( p q r ) having angles pi/p, pi/q, pi/r ... every finite group of
rotations is ...[ 1:2 ]... homomorphic to a finite group of
unit quaternions including the 'central' quaternion -1 ...
...
every finite reflection group has a subgroup of index 2
which is a rotation group, generated by products of pairs of
reflections. ... A convenient symbol for this rotation group
of order 2s is (p,q,r) ...
the tetrahedral group (3,3,2) of order 12,
the octahedral group (4,3,2) of order 24,
the icosahedral group (5,3,2) of order 60
... are subgroups of index 2 in ...
[3,3]
[4,3]
[5,3] respectively ...
...
We shall ... use the symbol GL(2,3) as an abbreviation
for ( C4 / C2 ; <4,3,2> / <3,3,2> ) ... where ... <3,3,2> ...
is a normal subgroup of ... <4,3,2> ... whose quotient group
is ...[ C4/2 ]... the order of ... ( C4 / C2 ; <4,3,2> / <3,3,2> )
... is ...[ 2 ]... times the order of ... <3,3,2> ...
... Apart from the little complication caused
by the common element -1 of ... C4 ... and ... <4,3,2> ...
we have here an instance of a 'subdirect product' ...
Corresponding to each group [p,q] of order 4s, generated by
reflections in three planes of Euclidean 3-space,
there is a group ... of order 8s, generated by reflections
in three lines of the unitary plane. In this manner ...
[3,3] yields ( C4 / C2 ; <4,3,2> / <3,3,2> ) = GL(2,3) ...".
(3,3,2) = A4 is order 12 tetrahedral rotations (without reflections)
[3,3] is order 24 tetrahedral rotations and reflections
<3,3,2> = SL(2,3) order 24 binary tetrahedral (quaternionic) group
= vertices of 24-cell in quaternionic space
336 elements of SL(2,7)include
<4,3,2> = order 48 binary octahedral (quaternionic) group
= vertices of 24-cell and its dual 24-cell
<3,3,2> = SL(2,3) order 24 binary tetrahedral (quaternionic) group
= vertices of 24-cell
[3,3] = order 24 Euclidean tetrahedral reflection group
and
cover 2:1 all 168 elements of PSL(2,7) = SL(3,2) = Klein Quartic
including
24-element octahedral (4,3,2) = S4
and
12-element tetrahedral (3,3,2) = A4
This brings to mind some further questions: Since
1 copy of binary tetrahedral = 1 x 24 = 24-element SL(2,3)
and
7 copies of binary octahedral = 7 x 48 = 336-element SL(2,7)
then:
Can you say that the 4 faces of the tetrahedron
are like the 4 dimensions of quaternions
with the 3 of SL(2,3) being the 3 quaternion imaginaries ?
Is the 1 copy due to the 1 associative triangle that
can be constructed from the 3 imaginary quaternions ?
Can you say that the 8 faces of the octahedron
are like the 8 dimensions of octonions
with the 7 of SL(2,7) being the 7 octonion imaginaries ?
Are the 7 copies due to the 7 associative triangles that
can be constructed from the 7 imaginary octonions ? ]
... Egan was able to spot a hidden cube lurking in his
picture ... each corner of his tetrahedral gadget is made of a
little triangular prism with one triangle facing out and one
facing in: for example, the pink triangle staring you right in the
face, or the light blue one on top. Since 4 x 2 = 8, there are 8
of these triangles. Abstractly, we can think of these as the 8
corners of a cube ... The way these 8 triangles come in pairs
corresponds to how the vertices of a cube come in diagonally
opposite pairs ... you can even draw a picture of a cube
on the Klein quartic by drawing suitable curves that connect the
centers of these 8 triangles ... If we gave the Klein quartic the
metric it inherits from the hyperbolic plane, the edges of the
cube would be geodesics. ...
... The Klein quartic is tiled by 56 triangles. 8 of them give
the cube we've just been discussing. In Egan's picture these
triangles look special, since they lie at the corners of his
tetrahedral gadget. But this is just an illusion caused by
embedding the Klein quartic in 3d space. In reality, the Klein
quartic is perfectly symmetrical: every triangle is just like
every other. So in fact there are lots of these cubes, and every
triangle lies in some cube. ... In fact, each triangle lies in
just one cube. So, there's precisely one way to take the
56 triangles and divide them into 7 bunches of 8 so that each
bunch forms a cube. So: the symmetry group of the Klein quartic
acts on the set of cubes, which has 7 elements.
... this symmetry group also acts on the Fano plane, which has
7 points. This suggests that cubes in the Klein quartic naturally
correspond to points of the Fano plane. And Egan showed this is
true! ... The Fano plane also has 7 lines. What 7 things in the
Klein quartic do these lines correspond to? Anticubes!
You see, the cubes in the Klein quartic have an inherent
handedness to them. You can go between the 8 triangles of a given
cube by following certain driving directions, but these driving
directions involve some left and right turns. If you follow the
mirror-image driving directions with "left" and "right" switched,
you'll get an anticube. Apart from having the opposite
handedness, anticubes are just like cubes. In particular, there's
precisely one way to take the 56 triangles and divide them into 7
bunches of 8 so that each bunch forms an anticube. Here's a
picture:
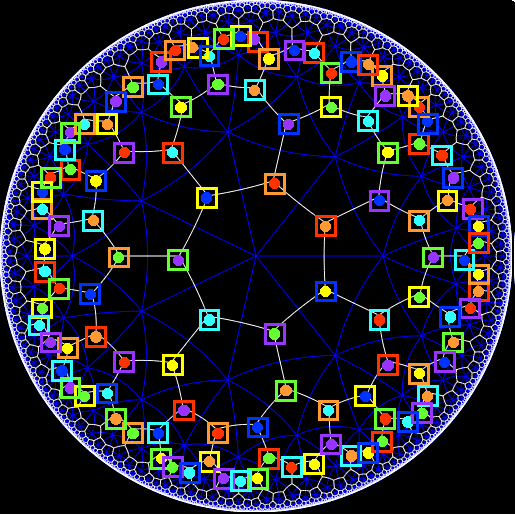
... Each triangle has a colored circle and a colored square on
it. There are 7 colors. The colored circle says which of the 7
cubes the triangle belongs to. The colored square says
which of the 7 anticubes it belongs to. If you stare at
this picture for a few hours, you'll see that each cube is
completely disjoint from precisely 3 anticubes. Similarly, each
anticube is completely disjoint from precisely 3 cubes. This is
just like the Fano plane, where each point lies on 3 lines, and
each line contains 3 points! So, we get a vivid way of seeing how
every figure in the Fano plane corresponds to some figure in the
Klein quartic curve. This is why they have the same symmetry
group.
... Here we are beginning to see how two superficially
different geometries are secretly the same:
FANO PLANE KLEIN'S QUARTIC CURVE
7 points 7 cubes
7 lines 7 anticubes
incidence of points and lines disjointness of cubes and anticubes
However, we're only half done! We've seen how to translate
simple figures and indicence relations in the Fano plane to
complicated ones in Klein's quartic curve. But, we haven't figured
out translate back!
KLEIN'S QUARTIC CURVE FANO PLANE
24 vertices ???
84 edges ???
56 triangular faces ???
incidence of vertices and edges ???
incidence of edges and faces ???
Here I'm talking about the tiling of Klein's quartic curve by
56 equilateral triangles. We could equally well talk about its
tiling by 24 regular heptagons, which is the Poincare dual. Either
way, the puzzle is to fill in the question marks. I don't know the
answer!
To conclude - at least for now - I want to give the driving
directions that define a "cube" or an "anticube" in Klein's
quartic curve. Say you're on some triangle and you want to get to
a nearby triangle that belongs to the same cube. Here's what you
do:
- hop across any edge,
- turn right,
- hop across the edge in front of you,
- turn left,
- then hop across the edge in front of you.
Or, suppose you're on some triangle and you want to get to
another that's in the same anticube. Here's what you do:
- hop across any edge,
- turn left,
- hop across the edge in front of you,
- turn right,
- then hop across the edge in front of you.
(If you don't understand this stuff, look at the picture above
and see how to get from any circle or square to any other circle
or square of the same color.)
You'll notice that these instructions are mirror-image versions
of each other. They're also both 1/4 of the "driving directions
from hell" that I described last time. In other words, if you go
LRLRLRLR or RLRLRLRL, you wind up at the same triangle you started
from. You'll have circled around one face of a cube or anticube!
In fact, your path will be a closed geodesic on the Klein quartic
curve... like the long dashed line in Klein and Fricke's original
picture ...

...".
In his 20 April 2005 Week
214, John Baez
says:
"... each heptagon [ in the picture immediately above
from Week
215 ] ... has been "barycentrically subdivided" into 14
right triangles. But don't worry about that yet; concentrate on
the heptagons. There's a blue heptagon in the middle, 7 red ones
touching that, 7 yellow ones touching those, then 7 green ones
falling off the edge of the picture, and 2 blue ones broken into
bits all around the corners of the picture. That's a total of 24
heptagons.
We wrap this thing up into a 3-holed torus using the numbers on
the edges of the picture:
- connect edges 1 and 6
- connect edges 3 and 8
- connect edges 5 and 10
- connect edges 7 and 12
- connect edges 9 and 14
- connect edges 11 and 2
- connect edges 13 and 4
In other words, connect edges n and n+5 mod 14. To connect them
the right way, make sure that triangles of the same color never
touch each other. ... Ignore the little triangles; just pay
attention to the heptagons! Then:
- Start on any edge of any heptagon and march along in either
direction.
- Then, when you get to the end, turn left.
- Then, when you get to the end, turn right.
- Then, when you get to the end, turn left.
- Then, when you get to the end, turn right.
- Then, when you get to the end, turn left.
- Then, when you get to the end, turn right.
- Then, when you get to the end, turn left.
- Then, when you get to the end, turn right.
- You should now be back where you started!!!
These are like the driving directions the devil gives people
who ask the way out of hell. LRLRLRLR and you're right back where
you started. But the resulting Platonic surface is heavenly. It
has lots of symmetries. Each of the 24 heptagons has 7-fold
rotational symmetry - and amazingly, all these rotations extend to
a symmetry of the Platonic surface!
Moreover, if you do any of these rotations and then do another
one centered at some other heptagon, you get another rotation
centered at another heptagon. So, our Platonic surface has a
symmetry group with 7 x 24 = 168 elements! These are all the
symmetries except for reflections. If we include reflections, the
symmetry group has size 168 x 2 = 336.
Now let's talk about those little triangles. Since our surface
is made of 24 heptagons, each chopped into 14 right triangles,
there are a total of 24 x 14 = 336 triangles. This is just the
number of symmetries!
This is no coincidence. We can specify a symmetry by saying
where it sends our favorite right triangle. Since it can go to any
other triangle, there are 336 possibilities.
By the way, this trick works for ordinary Platonic solids as
well. For example, if we take a dodecahedron and barycentrically
subdivide all 12 pentagons, we get 10 x 12 = 120 right triangles.
If we pick one of these as the "identity element", we can specify
any symmetry by saying which triangle this triangle gets sent to.
So, the set of triangles becomes a vivid picture of the
120-element symmetry group of the dodecahedron. It's called the
"Coxeter complex". This idea generalizes in many directions, and
is incredibly useful.
Anyway... there is much more to say about this stuff. For
example, if we take our hyperbolic plane tiled with heptagons
and count them grouped according to how far they are from the
central one, we get the sequence 7, 7, 14, 21, 35, 56, 91, ....
These are 7 times the Fibonacci numbers!
If we think of the hyperbolic plane as the unit disc in the
complex plane, this surface becomes a "Riemann surface", meaning
that it gets equipped with a complex structure. This was Felix
Klein's viewpoint when he discovered all this stuff in about 1878.
He showed this surface could be described by an incredibly
symmetrical quartic equation in 3 complex variables: u^3 v + v^3 w
+ w^3 u = 0 where we count two solutions as the same if they
differ by an overall factor. So, it's called "Klein's quartic
curve". ...
... Klein's quartic curve turns out to have the maximum number
of symmetries of any 3-holed Riemann surface.
... There's only one way to make a sphere into a Riemann
surface - it's called the Riemann sphere. You can think of it as
the complex numbers plus a point at infinity. This has infinitely
many symmetries. They're called conformal transformations, and
they all look like this:
az + b
z |---> --------
cz + d
They form a group called PSL(2,C), since it's the same as the
group of 2x2 complex matrices with determinant 1, mod scalars.
It's also the same as the Lorentz group!
There are different ways to make a torus into a Riemann
surface, some with more symmetries than others (see "week
124"). But, there are always translation symmetries in both
directions, so the symmetry group is always infinite.
On the other hand, a Riemann surface with 2 or more holes can
only have a finite group of conformal transformations. In fact, in
1893 Hurwitz proved that a Riemann surface with g holes has at
most 84(g - 1) For g = 3, this is 168. So, Klein's quartic surface
is as symmetrical as possible! (We don't count reflections here,
since they don't preserve the complex structure - they're like
complex conjugation.)
... Sitting inside PSL(2,C) is PSL(2,Z), where we only use
integers a,b,c,d in our fractional linear transformation
az + b
z |---> --------
cz + d
This subgroup acts on the upper half-plane H, which is just
another way of thinking about the hyperbolic plane.
Sitting inside PSL(2,Z) is a group G(7) consisting of guys
where the matrix
a b
c d
is congruent to the identity:
1 0
0 1
modulo 7. This is an example of a "congruence subgroup"; these
serve to relate complex analysis to number theory in lots of cool
ways. In particular, Klein's quartic curve is just H / G(7) Since
G(7) is a normal subgroup of PSL(2,Z), the quotient group
PSL(2,Z)/G(7) = PSL(2,Z/7) acts as symmetries of Klein's quartic
curve. And, this group has 168 elements!
In fact, this group is the second smallest nonabelian simple
group. The smallest one is the rotational symmetry group of the
icosahedron, which has 60 elements. This group is actually
PSL(2,Z/5), and Klein had run into it in his work on the
icosahedron and quintic equations (see "week
213"). So, it's actually far from sheer luck that he then
moved on to PSL(2,Z/7) and ran into his wonderful quartic curve.
By the way, this 168-element group is also known as PSL(3,Z/2) -
the symmetry group of the "Fano plane". This is a name for the
projective plane over Z/2. The Fano plane is closely related to
the octonions ... in fact, our 168-element group acts on the
set of octonion multiplication tables...
... when
you pack spheres as densely as possible in 8 dimensions, each
sphere touches 240 others... and if you look at the 240 neighbors
of a given sphere, each one of those neighbors touches 56 other
neighbors ... this gives rise to a 56-dimensional representation
of the exceptional group E7 - its smallest nontrivial
representation! And, how it gives rise to a 57-dimensional
manifold on which the exceptional group E8 acts - the smallest
space on which it acts nontrivially! ...
... Having the number 56 on my brain, I can't resist noting
that if you take Klein's quartic curve tiled by heptagons, and you
count the vertices, you get 24 x 7 / 3 = 56 since each vertex is
shared by 3 heptagons. ...".
Tony Smith's Home Page