Deriving the Standard Model plus Gravitation
from Simple Operations on Finite Sets
by Tony Smith
Table of Contents:
Chapter 1 - Introduction.
Chapter 2 - From Sets to Clifford Algebras.
Chapter 3 - Octonions and E8 lattices.
Chapter 4 - E8 spacetime and particles.
Column Spinors and Fermions.
Row Spinors and Vector Spacetime.
Dimensional Reduction
Spinors and Papapetrou Equations.
Bivector Gauge Bosons and Higgs Scalar.
Conformal Moebius Clifford Transformations
Clifford Algebras
Division Algebras
Weyl Groups and Root Vectors
gluon confinement
Casimir operators and questions of signature.
Complex Domains and Shilov Boundaries.
Other Multivectors.
Subtle Triality Supersymmetry.
Ultraviolet Finiteness and Renormalization.
Chapter 5 - HyperDiamond Lattices.
Chapter 6 - Spacetime and Internal Symmetry Space.
Chapter 7 - Feynman Checkerboards.
Chapter 8 - Charge = Amplitude to Emit Gauge Boson.
Chapter 9 - Mass = Amplitude to Change Direction.
Chapter 10 - Protons, Pions, and Physical Gravitons.
Appendix A - Errata for Earlier Papers.
References.
Here is how it works from various viewpoints:
We have 8 gammas (1,2,3,4,5,6,7,8) in our Cl(8) Clifford algebra.
The 15 with index 6 or less give the conformal group and gravity.
The 13 left over do not form any subgroup of the 28-dim Spin(8) rotations of 8-dim spacetime, so break the symmetry of 8-dim spacetime into
plus
a 4-dim internal symmetry space that is the space of colors (red, green, blue, and neutral=black).
Then notice that 8 of the 13 involve one spacetime index and one color internal symmetry index. Let them be the 8 color force gluons. Since they are rotations in one spacetime dimension and one color internal symmetry dimension, you might ask:
The answer is: Gluons are confined to the interior of protons, pions, etc. You have to look inside them to see gluons flying around changing colors.
The remaining 5 of the 13 do not involve any spacetime index, so that they can act as conventional gauge bosons whose rotations are confined to the internal symmetry space.
Let 4 of them be the generators of the U(2) = SU(2)xU(1) electroweak force.
As for the last one, the 13th, let it represent the U(1) phase of particle propagators.
Here are more details:
Let 4 of the 8 basis elements of the Cl(8) Clifford algebra, say (0,2,3), correspond to 4-dim physical spacetime, in a straightforward way:
Now, let the other 4, that is, (4,5,6,7) correspond to color space which will be an internal symmetry space. Take as colors red, green, and blue (r,g,b). Let the 4th color be black (k, to distinguish its letter from b=blue). Make this correspondence a little more complicated than (0,1,2,3,) = (x,y,z,t) as follows:
This way, we have 2 colorless basis elements (k,w) and 2 colored ones (r,b). Of course, you can make green from w and r and b, so you have all colors. The basis is
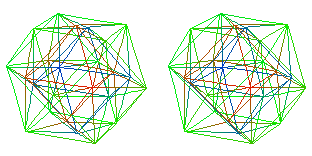
Now look at the structure of the 28 bivectors, the generators of Spin(8).
Just as the 8+8 = 16 first-generation fermion particles and anti-particles, and 8-dimensional spacetime (reduced to 4-dimensional physical spacetime plus 4-dimensional internal Symmetry Space) can be represented by a 24-cell,
24 of the 28 gauge boson Spin(8) generators of the D4-D5-E6-E7-E8 VoDou Physics model can be represented by the vertices of a dual 24-cell:

The 24 vertices of the 24-cell are the 24-vertex root vectors of the D4 Spin(8) Lie algebra in 4-dimensional root vector space with 4 origin root vectors. The 28 infinitesimal generators correspond to the bivector indices
01 02 03 04 05 06 07 12 13 14 15 16 17 23 24 25 26 27 34 35 36 37 45 46 47 56 57 67
which can be regarded as the upper triangular part of an 8x8 antisymmetric real matrix.
The 4 origin root vectors can correspond to
01 23 45 67
and the 24-cell vertices can correspond to
02 03 04 05 06 07 12 13 14 15 16 17 24 25 26 27 34 35 36 37 46 47 56 57
In terms of the basis (x,y,z,t,k,w,r,b), they are
xy xz xt xk xw xr xb yz yt yk yw yr yb zt zk zw zr zb tk tw tr tb kw kr kb wr wb rb
The 6 that involve only (0,1,2,3) = (x,y,z,t) form the Lorentz boosts and rotations of physical spacetime:
xy xz xt yz yt zt
Note that (01,02,12) = (xy,xz,yz) are rotations and (03,13,23 ) = (zt,yt,zt) are Lorentz boosts.
Now let them interact with 4 = k. Since it is colorless, moving in 5-space (k-space) does not change the color of anything, so it can be regarded as just an "extra" dimension added to 4-dim spacetime in which "rotations" look like translations, and we then get the 10 with indices 0,1,2,3,4 which are taken to be generators of deSitter/Poincare gravity:
01 02 03 04 12 13 14 23 24 34
or
xy xz xt xk yz yt yk zt zk tk
Note that (04,14,24,34) = (xk, yk, zk, tk) are translations. Next let the 10 interact with 5 = (r+g+b) = w. Since it is also colorless, moving in 6-space (w-space) does not change the color of anything, so it can also be regarded as just an "extra" dimension. In it "rotations" look like conformal transformations (1 dilation and 4 special conformal transformationsi), and we then get the 15 with indices 0,1,2,3,4,5 which are taken to be generators of Segal's conformal Spin(2,4) = SU(2,2) which can also be gauged to produce gravity:
01 02 03 04 05 12 13 14 15 23 24 25 34 35 45
or
xy xz xt xk xw yz yt yk yw zt zk zw tk tw kw
Note that the 45, which is only in (k,w) space, corresponds to the dilation and (05,15, 25, 35) = (xw, yw, zw, tw) are the 4 special conformal transformations.
Also note that the Weyl root vector polytope of D3=A3 Spin(2,4) = SU(2,2) is the 3-dimensional cuboctahedron, and that it can be taken to be the central (green) cuboctahedron of the 4-dim 24-cell root vector polytope of Spin(8).

That leaves 13 generators left over, those with at least one index 6 or 7
06 07 16 17 26 27 36 37 46 47 56 57 67
or
xr xb yr yb zr zb tr tb kr kb wr wb rb
and it would be nice if 12 of them could represent the generators of the SU(3) x SU(2) x U(1) Standard Model.
(In these remarks I am using Euclidean signature.)
For a first reason, physically at low energies you don't want to see color charges, which should be confined to the interior of hadrons. Therefore, since 15-dim Spin(6)
xy xz xt xk xw yz yt yk yw zt zk zw tk tw kw
does NOT involve the indices r and b that are not color-neutral, you can use it, but you cannot go to 21-dim Spin(7) becaus, if you do, you must involve an index r that is not color-neutral:
xy xz xt xk xw xr yz yt yk yw yr zt zk zw zr tk tw tr kw kr wr
For a second reason, you want the group to have a natural action on the 4-dim spacetime that is physical at low energies:
- 6-dim Spin(4) acts naturally on 4-dim spacetime because it is just Lorentz boosts and rotations on 4-dim spacetime;
- 10-dim Spin(5) acts naturally on 4-dim spacetime because it acts globally on the symmetric space Spin(5) / Spin(4) = S4, and also, there is an isomorphism Spin(5) = Sp(2), so that Spin(5) globally on the symmetric space Sp(2) / Sp(1)xSp(1) = QP1 (where QP1 is quaternionic projective 1-space). Note that Sp(1) = Spin(3) = SU(2) = S3, and that Sp(1)xSp(1) = Spin(4), and that QP1 = S4.
- 15-dim Spin(6) acts naturally on 4-dim spacetime because there is an isomorphism Spin(6) = SU(4), so that Spin(6) acts naturally on the 4-dim fundamental repesentation space of SU(4).
- However, 21-dim Spin(7) has no isomorphism that allows it to act naturally on 4-dim spacetime.
- It acts naturally on the 7-dim vector space of which it is the covering of the rotation group, and
- it acts naturally on the 7-dim symmetric space Spin(7) / G2, and
- it acts naturally on the 6-dim symmetric space Spin(7) / Spin(6),
but Spin(7) does not have a natural full action on a 4-dim spacetime.
xr xb yr yb zr zb tr tb kr kb wr wb rb
To see this, notice that they have a natural interpretation in terms of symmetric spaces, as the coset space
is 28 - 16 = 12-dimensional. If you let the 67 (or rb) correspond to the U(1), then the other 12 of the 13 left-over generators form the 12-dim symmetric coset space Spin(8)/Spin(6)xU(1). It is only a coset space, so it does NOT directly inherit the commutator relations of Spin(8) and does NOT directly form a Lie subalgebra of Spin(8).
As David Finkelstein has said: "... They cannot do this [form a Lie subalgebra of Spin(8)] exactly. For example, no one of the 13 commutes with all the rest, as the generator of U(1) does. Nor do the last 13 commute with the first 15 conformal generators as the SU(3) x SU(2) x U(1) generators do. ...".
The way to get the 12 to represent the Standard Model is to assign commutation relations to the 12 that are inherited from the Weyl group symmetry of Spin(8).
To see how this works, begin by breaking the symmetry of the 8-dim spacetime by splitting it into two separate 4-dim spaces as described above, so that
breaks down to
What is the physics of this breakdown, at our low energies where it has occurred ?
The Lorentz, deSitter, and conformal structures with indices 0,1,2,3,4,5 work as described above.
Now, look at the 13 generators left over, those with at least one index 6 or 7.
Only one of them, 67 or rb, involves ONLY the dimensions that are NOT involved in the 15-dim Conformal group.
Let 67 = rb represent the U(1) phase of particle propagators.
That leaves 12 generators:
06 07 16 17 26 27 36 37 46 47 56 57
or
xr xb yr yb zr zb tr tb kr kb wr wb
Note that these 12 correspond to the two octahedra
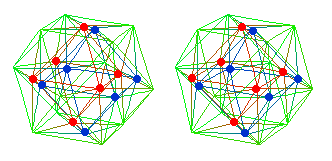
that remain after deleting the central cuboctahedron from the 24-cell root vector polytope of Spin(8).
Set the common axis of the two octahedra such that the 4 vertices on it are the 4 vertices involving k and w:
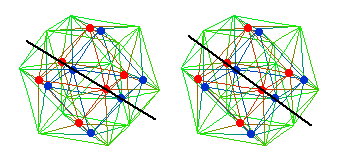
The remaining 8 vertices
xr xb yr yb zr zb tr tb
correspond to the 8 gluons of the SU(3) color force. They each have one color dimension and one spacetime dimension, so that they represent rotation in two dimensions, one color and one spacetime, thus mixing color and spacetime.
Because gluons are confined within protons, pions, and other particles containing them, such effects can only be seen inside protons, pions, etc. The corresponding quark/hadron phase transition may be a tzimtzum Rekiah.
The 8 vertices that are off the common axis of the two octahedra
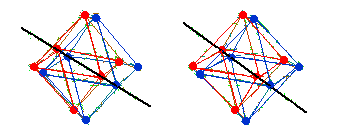
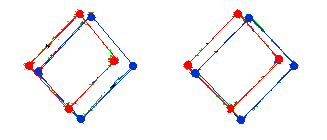
can be considered as the vertices of a cube:
tb----xb |\ | \ | zb----yb | | | | yr-|--zr | \| \| xr----tr
Now look at the cube along its tb-tr diagonal axis, and project all 8 vertices onto a plane perpendicular to the tb-tr axis, giving the diagram
yb xb zb tb tr zr xr yr
with two central points surrounded by two interpenetrating triangles, which is the root vector diagram of SU(3), from which commutation relations of SU(3) can be constructed for {tb,tr,xb,yb,zb,xr,yr,zr).
Since each gluon links 4-dim spacetime to color internal symmetry space, the gauge group SU(3) acts globally on CP2 Internal Symmetry Space, as can be seen by the fibration
Now go back and look at the 4 vertices on the common axis of the two octahedra,

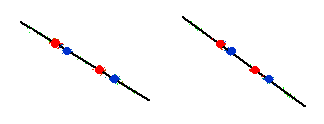
that is, the 4 vertices involving k and w.
kr kb wr wb
They correspond to the 3 weak bosons and the electromagnetic photon. They each have one color dimension and one spacetime dimension, so that they represent rotation in two dimensions, both of which are in internal symmetry space, so there is no mixing of spacetime and internal symmetry space, and they can be treated as conventional gauge bosons that are the generators of electroweak U(2) = SU(2) x U(1).
All 4 of them are on a line (the Z-axis of the (X,Y,Z) space of the two octahedra). Put the two involving w at the ends of a line segment, with the two involving k at the origin center of a line segment, thus getting the root vector diagram of U(2) = SU(2) x U(1), which is the sum of the root vector diagrams of A1=B1=C1 and A0=D1.
kr kb wr wb
A correspondence with the electroweak gauge bosons is then:
Note that each of the neutral bosons (Z0 plus photon) corresponds to a rotation in the colorless color-neutral k-space part of internal symmetry space that corresponds to translations.
Also note that each of the electric-charged W+ and W- bosons corresponds to a rotation in the colorful color-neutral w-space part of internal symmetry space that corresponds to conformal transformations.
These correspondences may be related to:
Since each weak boson and photon acts entirely within color internal symmetry space, the gauge group U(2) acts locally on CP2 Internal Symmetry Space, as can be seen by the fibration
( Global Group Structure of the Standard Model is discussed here.)
If you combine the 15 Conformal generators with the 67 = rb generator of the U(1)particle propagator phase, you get SU(2,2) x U(1) = U(2,2), so that
we have decomposed the 28 generators of Spin(8) into:
16 generators of U(2,2) = U(1)xSU(2,2) = U(1)xSpin(2,4) for propagator phase, Gravity, and the Higgs Mechanism, acting on 4-dimensional Spacetime.8 generators of SU(3) for the Color Force, acting on 4-dimensional Internal Symmetry Space.
4 generators of U(2) = U(1)xSU(2) for Electromagnetism and the Weak Force, acting on 4-dimensional Internal Symmetry Space.
From Sets to Quarks: Table of Contents: Chapter 1 - Introduction. Chapter 2 - From Sets to Clifford Algebras. Chapter 3 - Octonions and E8 lattices. Chapter 4 - E8 spacetime and particles. Chapter 5 - HyperDiamond Lattices. Chapter 6 - Spacetime and Internal Symmetry Space. Chapter 7 - Feynman Checkerboards. Chapter 8 - Charge = Amplitude to Emit Gauge Boson. Chapter 9 - Mass = Amplitude to Change Direction. Chapter 10 - Protons, Pions, and Physical Gravitons. Appendix A - Errata for Earlier Papers. References.
......