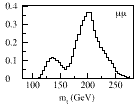
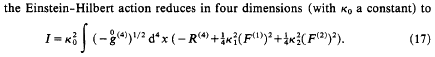CDF and D0 observed 3 peaks in their T-quark
data:
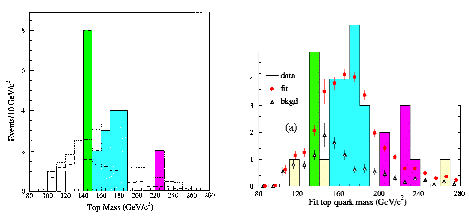
The middle (cyan) peak ( around 175
GeV ) is the one they initially identified as the T-quark.
The low peak (green) and the high
peak (magenta) can be understoon in
terms of Froggatt's paper hep-ph/0307138:
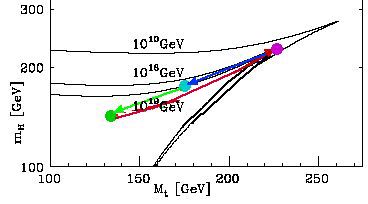
in terms of a 3-part system of the T-quark, the Higgs, and the
Triviality Bound.
The high and
low peaks can be seen when you look
closely at dilepton events, such as the D0 event Run 84395, Event
15530 ( mu mu ) described in the
1997 UC Berkeley PhD thesis of Erich Ward Varnes and in hep-ex/9808029
as analyzed using the matrix-element weighting algorithm that,
according to hep-ex/9808029,
"... is an extension of the weight proposed in [R.H. Dalitz and
G.R. Goldstein, Phys. Rev. D45, 1531 (1992)] ...".
Koichi Yamawaki in his paper at
hep-ph/9603293
describes T-quark condensate Higgs models ( NJL and BHL ) that seem
to be related to the low and
high T-quark peaks
and
In his paper, Yamawaki says in part:
"... tightly bound composite Higgs models such as ... top
quark condensate ...[which have]... nontrivial short
distance dynamics of the gauged Nambu-Jona-Lasinio (NJL) models
(gauge theories plus four- fermion interactions)
[ In an 8-dimensional Kaluza-Klein
version the four-fermion interaction is not needed. ]
... in which the critical phenomenon in the gauged NJL
model [yield] a simple reason why the top quark can have
an extremely large mass compared with other quarks and leptons.
... the four-fermion theory
[ In an 8-dimensional Kaluza-Klein
version the four-fermion interaction is not needed. ]
in the presence of gauge interactions (gauged NJL model)
can become renormalizable and nontrivial in sharp contrast to the
pure NJL model without gauge interactions. ...
... The Higgs boson was predicted as a tbar-t bound state
...
... the top quark can have a large mass, or more properly, why
other fermions can have very small masses ... if only the top
quark coupling is above the critical coupling, while all others
[are] below it ...
The top quark condensate ... indeed yields a standard gauge
symmetry breaking pattern ... to feed the mass of W and Z bosons.
...
The largest physically sensible (new physics scale) would be
the Planck scale 10^19 GeV at which we have a minimum value
prediction mt = 145 GeV ... with the
pure NJL case ...
The BHL [ Bardeen-Hill-Lindner ] value is then given by
mt = 218 +/- 3 GeV, at 10^19 GeV ...
The Higgs boson was predicted as a tbar-t bound state ... Its mass
was also calculated by BHL through the full RG equation ... the
result being ... MH = mt x 1.1 at 10^19 GeV ...[which
gives]... MH = 239 +/- 3 GeV for mt =
218 +/- 3 GeV ...[ and MH = 143 GeV for
mt = 130 GeV which is reasonably
close to the 145 GeV value of mt ]...".
In other words, Yamawaki indicates
that
the BHL model describes the high T-quark peak around
218 GeV and
the BHL model Higgs / T-quark mass ratio of 1.1 is
consistent with the 145.8 GeV / 130 GeV = 1.12 ratio of the
D4-D5-E6-E7-E8 VoDou physics model.
Also, Hashimoto, Tanabashi, and Yamawaki
in their paper at hep-ph/0311165
say:
"... We perform the most attractive channel (MAC)
analysis in the top mode standard model with TeV-scale
extra dimensions, where the standard model gauge bosons and
the third generation of quarks and leptons are put in
D(=6,8,10,...) dimensions. In such a model, bulk gauge couplings
rapidly grow in the ultraviolet region. In order to make the
scenario viable, only the attractive force of the top condensate
should exceed the critical coupling, while other channels such as
the bottom and tau condensates should not. We then find that the
top condensate can be the MAC for D=8 ... We predict masses of the
top (m_t) and the Higgs (m_H) ... based on the renormalization
group for the top Yukawa and Higgs quartic couplings with the
compositeness conditions at the scale where the bulk top condenses
...
for ...[ Kaluza-Klein
type ]... dimension... D=8 ... m_t =
172-175 GeV
and m_H=176-188 GeV ...".
The middle peak can be seen when you
look closely at the D0 dilepton event Run 84395,
Event 15530 ( mu mu ) described in the
1997 UC Berkeley PhD thesis of Erich Ward Varnes and in hep-ex/9808029

using the neutrino weighting algorithm. It has 3 jets. If all 3
jets are included ( the solid line in the graph ), energy around
200 GeV, corresponding to the Standard
Model Critical Point Truth Quark excited state at the
magenta dot. If only the 2 highest
energy jets are included ( the dashed line in the graph ), it has
energy around 170 GeV, corresponding to
the 2-vacuum intermediate excited Truth Quark state at the
cyan dot, and the energy of the third
jet would correspond to decay down the blue
curve along the Vacuum Stability bound of 10^19 GeV.
Here are some more details from
Yamawaki's paper at hep-ph/9603293:
"... mass of all particles in the ... standard model (SM)
... is attributed to a single order parameter, the vacuum
expectation value (VEV) of the Higgs doublet. Thus the problem of
the origin of mass is simply reduced to understanding the dynamics
of the Higgs sector...
... the situation very much resembles the Ginzburg-Landau
(GL)'s macroscopic theory for the superconductivity, the
mysterious parts of which were eventually explained by the
microscopic theory of Bardeen-Cooper-Schrieffer (BCS): The GL's
phenomenological order parameter was replaced by the Cooper pair
condensate due to the short range attractive forces.
... the sigma-model description by Gell-Mann and Levy (GML)
works very well as far as the low energy (macroscopic) phenomena
are concerned, while the deeper understanding of it was first
given by Nambu and Jona-Lasinio (NJL)1 based on the analogy with
the BCS dynamics.
Nowadays people believe that essentially the same phenomena as
described by the NJL paper takes place in the microscopic theory
for hadrons, QCD.
In QCD the VEV of sigma ... 93 MeV, has been replaced by the
quark-antiquark pair condensate ... an analogue of the Cooper pair
condensate, formed by the attractive color forces.
The Nambu-Goldstone (NG) boson, the pion, is now a composite
state of quark and antiquark.
This is actually the prototype of the dynamical symmetry
breaking (DSB) due to composite order parameters like fermion pair
condensates.
In fact Higgs sector in the SM is precisely the same as the
sigma model except that ... the VEV of sigma ... 93 MeV ... is now
replaced by the Higgs VEV ... 250 GeV ...
One is thus naturally led to speculate that there might exist a
microscopic theory for the Higgs sector, with the Higgs VEV being
replaced by the fermion-antifermion pair condensate ...
... tightly bound composite Higgs models were ... proposed
based on the ... gauged NJL model (gauge theory plus four-fermion
interaction)
[ In an 8-dimensional Kaluza-Klein
version the four-fermion interaction is not needed. ]
within the framework of ladder Schwinger-Dyson (SD)
equation. The gauged NJL model was shown to have a phase structure
divided by a critical coupling (critical line) similarly to the
NJL model, and have a large anomalous dimension due to strong
attractive forces at relatively short distance or high energy.
Such a system may actually be regarded as a theory with
ultraviolet fixed point(s) in contrast to the asymptotic freedom.
A remarkable feature of this dynamics is that the four-fermion
interation in four dimensions
[ In an 8-dimensional Kaluza-Klein
version the four-fermion interaction is not needed. ]
may become renormalizable ... in a non-perturbative sense
... in sharp contrast to the pure NJL model ...
... We give a detailed comparison between the original
formulation of Miransky-Tanabashi-Yamawaki (MTY) and another one
of Bardeen-Hill-Lindner (BHL) ...
... current
masses ... are entirely due to the Higgs VEV through
the Yukawa coupling in the Glashow-Salam-Weinberg model and
have nothing to do with the QCD dynamics ...
... QCD has no elementary order parameters. If the quark and
gluon fields were order parameters, then the Lorentz invariance,
color symmetry and charge symmetry would have been spontaneously
broken in QCD in contrast to the reality. Then only possible order
parameters are composite ones, variation of n-point Green
functions or that of local composite fields. ... where ... a
dynamical mass of quark, signals the spontaneous chiral symmetry
breaking due to the QCD dynamics. We may define an "on-shell"
dynamical mass m* ... which is often called constituent
mass ( it also includes the effects of the explicit
breaking due to the current mass). In contrast to the sigma
model where ... there is no Yukawa coupling ... at Lagrangian
level in QCD. However, we have an "induced" Yukawa vertex ...
which is a "wave function" of [ pi ] as a composite of
[ quark and antiquark ] and is related to the dynamical
mass ...
... As a low energy scale we take the scale parameter of QCD,
/\_QCD, which is typically of order 100 MeV - 1 GeV and actually
characterizes the scale of the order parameters ...[ pion
force ].. 93 MeV, ...[constituent light quarks ]...
300 MeV or ...[ /\_QCD = 250 MeV ]...
... Nambu-Jona-Lasinio Model ... the gauged NJL models
(gauge theories plus four-fermion theories) ...
[ In an 8-dimensional Kaluza-Klein
version the four-fermion interaction is not needed. ]
... encompass a variety of tightly bound composite Higgs
models, such as .. top quark condensate ...[ with anomalous
dimension 2 ]... The NJL model is of course non-renormalizable
and trivial theory, i.e., we cannot take the UV cutoff to infinity
to have a sensible continuum theory, in contrast to the gauged NJL
model ...
... Gauged Nambu-Jona-Lasinio Model ...
... Tightly Bound Composite Higgs Models ... There are a
variety of tightly bound composite Higgs models based on the
gauged NJL model ... top quark condensate ...[ with anomalous
dimension 2 ]...
... Top Quark Condensate ... the ... extremely large ...
top quark ... mass ... compared with mass of all other quarks and
leptons and seems to suggest a special role of the top quark in
the electroweak symmetry breaking, the origin of mass, and hence a
strong connection with the Higgs boson itself. ... the top quark
condensate proposed by Miransky, Tanabashi and Yamawaki (MTY) and
by Nambu independently ... entirely replaces the standard Higgs
doublet by a composite one formed by a strongly coupled short
range dynamics (four-fermion interaction)
[ In an 8-dimensional Kaluza-Klein
version the four-fermion interaction is not needed. ]
which triggers the top quark condensate. The Higgs boson
emerges as a tbar-t bound state and hence is deeply connected with
the top quark itself. ... MTY introduced explicit four-fermion
interactions
[ In an 8-dimensional Kaluza-Klein
version the four-fermion interaction is not needed. ]
responsible for the top quark condensate in addition to
the standard gauge couplings. Based on the explicit solution of
the ladder SD equation, MTY found that even if all the
dimensionless four-fermion couplings
[ In an 8-dimensional Kaluza-Klein
version the four-fermion interaction is not needed. ]
are of O(1), only the coupling larger than the critical
coupling yields non-zero (large) mass ... The model was further
formulated in an elegant fashion by Bardeen, Hill and Lindner
(BHL) in the SM language, based on the RG equation and the
compositenes condition. BHL essentially incorporates 1/Nc
sub-leading effects such as those of the composite Higgs loops and
... gauge boson loops which were disregarded by the MTY
formulation. We can explicitly see that BHL is in fact equivalent
to MTY at 1/Nc-leading order. Such effects turned out to reduce
the above MTY value 250 GeV down to 220
GeV ...
... Top Quark Mass Prediction ... the central part of
the ... MTY ... model ... relat[es]... the dynamical mass
of the condensed fermion (top quark) to the mass of W/Z bosons.
... the mass of W and Z bosons in the top quark condensate is
generated via dynamical Higgs mechanism .... where ... 250 GeV
...determine[s] the IR scale of the model ... we could
predict mt by fixing ... [t]he decay constants of these
composite NG bosons ...[about]... 250 GeV so as to have a
correct mW ... Actually, ... mt ...[is]
determine[d]... as a decreasing function of cutoff /\. The
largest physically sensible /\ (new physics scale) would be the
Planck scale /\ = 10^19 GeV at which we have a minimum value
prediction mt = 145 GeV. ... Now in
the gauged NJL model, QCD plus four-fermion interaction ...
[ In an 8-dimensional Kaluza-Klein
version the four-fermion interaction is not needed. ]
...[f]or the Planck scale cutoff /\ = 10^19 GeV,
we have mt = 250 GeV ... This is compared with the pure NJL
case mt = 145 GeV ...
... RG Equation plus Compositeness Condition (BHL) ...
the BHL formulation of the top quark condensate, which is based on
the RG equation combined with the compositeness condition ...
start[s] with the SM Lagrangian which includes explicit
Higgs field at the Lagrangian level ...
... BHL versus MTY ...MTY formulation is based on the
nonperturbative picture ... On the other hand, BHL is crucially
based on the perturbative picture ...[which]... breaks
down at high energy near the compositeness scale /\ ...[ 10^19
GeV ]... there must be a certain matching scale /\_Matching
such that the perturbative picture (BHL) is valid for mu <
/\_Matching, while only the nonperturbative picture (MTY) becomes
consistent for mu > /\_Matching ... However, thanks to the
presence of a quasi-infrared fixed point, BHL prediction is
numerically quite stable against ambiguity at high energy region,
namely, rather independent of whether this high energy region is
replaced by MTY or something else. ... Then we expect mt = mt(BHL)
= 1 Ã2yt(mu = mt) v = 1/(sqrt(2)) ybart v within 1-2%, where ybart
is the quasi-infrared fixed point given by Beta(ybart) = 0 in ...
the one-loop RG equation ... The composite Higgs loop changes
ybart^2 by roughly the factor Nc/(Nc +3/2) = 2/3 compared with the
MTY value, i.e., 250 GeV -> 250 x sqrt(2/3) = 204 GeV, while
the electroweak gauge boson loop with opposite sign pulls it back
a little bit to a higher value. The BHL value is then given by
mt = 218 +/- 3 GeV, at
/\ = 10^19 GeV.
The Higgs boson was predicted as a tbar-t bound state with a
mass MH = 2mt based on the pure NJL model calculation1. Its mass
was also calculated by BHL through the full RG equation ...
the result being ... MH / mt = 1.1 ) at /.\ = 10^19 GeV
...".
Here are some more details from the paper of
Hashimoto, Tanabashi, and Yamawaki at hep-ph/0311165:
"... The idea of the top quark condensate explains
naturally the large top mass of the order of the electroweak
symmetry breaking (EWSB) scale. In the explicit formulation of
this idea often called the "top mode standard model" (TMSM), the
scalar bound state of tbar-t plays the role of the Higgs boson in
the SM.
There are ... problems in the original version of the TMSM:
- We need to introduce ad hoc four-fermion interactions of
the top quark in order to trigger the EWSB.
- ... if we take /\ to the Planck ... scale ...[s]uch
a huge /\ ... causes a serious fine-tuning problem.
As a possible solution to these problems, following the line of
an earlier attempt of the TMSM in the TeV-scale extra dimension
[ Kaluza-Klein ] scenario
Arkani- Hamed, Cheng, Dobrescu and Hall (ACDH) proposed an
interesting version of such where the SM gauge bosons and the
third generation of quarks and leptons live in the D(= 6, 8,
· · · )-dimensional bulk, while the first and
second generations are confined in the 3-brane (4-dimensional
Minkowski space-time).
[ Compare the D4-D5-E6-E7-E8 VoDou
physics model. in which
where 4-dim PST and 4-dim ISS are the products of dimensional
reduction of a high-energy
8-dimensional SpaceTime. ]
Gauge interactions in higher dimensions than four become
strong in a certain high-energy region. Bulk gauge interactions
are expected to trigger the top condensation without adding ad hoc
four-fermion interactions, in contrast to the original version of
the TMSM.
However, the dynamics of bulk gauge theories was not concretely
analyzed ...[ by ACDH ]... In particular, as it turned out
the bulk QCD coupling, which is the most relevant interaction
for the top condensation, has an ultraviolet fixed point (UV-FP)
or upper bound within the same MSbar scheme of the truncated
Kaluza-Klein (KK) effective theory as that ...[ the work of
ACDH ]... was based on. Thus, it is quite nontrivial
whether the top condensation is actually realized or not.
... we have studied the dynamical chiral symmetry breaking
(DxSB) in bulk gauge theories, based on the ladder Schwinger-Dyson
(SD) equation. Switch ing off the electroweak interaction in the
bulk, we then found that the bulk QCD coupling can ... become
suffciently large to trigger the top condensation for ... D =
8.
For the purpose of model building, we further need to study the
effect of the bulk electroweak interactions: Since the bulk U(1)Y
interaction grows very quickly due to the power-like running
behavior and reaches immediiately its Landau pole /\_LY , it may
affect the most favored channel for condensate, i.e., the most
attractive channel (MAC). We also need to study whether or not the
prediction of the top mass agrees with the experiments.
... we demonstrate a possibility that the top condensate is
actually the MAC even including all of the bulk SM gauge
interactions. This is quite nontrivial, because inclusion of the
strong bulk U(1)Y interaction may favor the tau condensation
rather than the top condensation. In order for only the top quark
to acquire the dynamical mass of the order of the EWSB scale, the
binding strength should exceed the critical binding strength ...
only for the top quark ("topped MAC" or "tMAC"). Namely, our
scenario works only when... the binding strength... of the top ...
condensate...[exceeds]... the critical binding strength
...[which in turn exceeds]... the binding strength ... of
the ... bottom... and tau condensates at the scale /\, ... We
refer to the scale /\ satisfying ...[those
relationships]... as the tMAC scale /\_tM.
For the MAC analysis, we study binding strengths ... by
using the one-loop renormalization group equations (RGEs) of
dimensionless bulk gauge couplings. It is in contrast to the
analysis of ACDH where all of bulk gauge couplings are assumed
equal (and strong enough for triggering the EWSB). In order to
check reliability of our MAC analysis, we also study the
regularization-scheme dependence of the binding strengths. We
calculate gauge couplings in two prescriptions, the MSbar scheme
of the truncated KK effective theory and the proper-time (PT)
scheme.
There are some varieties in the estimation of ... the critical
binding strength ... The naive dimensional analysis (NDA) implies
... the critical binding strength ...[is about]... 1,
while the ladder SD equation yields much smaller value ... the
critical binding strength ...[about]... 0.1 . As the
estimate of ... the critical binding strength ... increases ...
the region of the tMAC scale gets squeezed. Even if we adopt the
lowest possible value of ... the critical binding strength ...
given by the ladder SD equation, we find that the tMAC scale does
not exist for the simplest scenario with D = 6. On the other hand,
the tMAC scale does exist in D = 8 for the value of the ladder
SD equation, /\_tM R = 3.5&endash;3.6, where the compactification
scale R^(-1) is taken to be 1-100 TeV. For D = 10, the MAC
analysis significantly depends on the regularization scheme.
Once we obtain the tMAC scale tM, we can easily predict the top
mass mt and the Higgs mass mH by using the renormalization group
equations (RGEs) for the top Yukawa and Higgs quartic couplings,
and the compositeness conditions at the scale /\ = /\_tM. This is
in contrast to the earlier approach ..[of ACDH]... where
the composite scale /\ is treated as an adjustable free parameter
and fixed so as to reproduce the experimental value of mt. Without
such an adjustable parameter, we predict the top quark mass
mt = 172 - 175
GeV for D = 8 and R^(-1) = 1-100 TeV.
... We find that the value of mt near the compactification
scale R^(-1) is governed by the quasi infrared fixed point (IR-FP)
for the top Yukawa coupling y ... We also predict the Higgs boson
mass as mH = 176 - 188 GeV ...[which is close to the range of
1.1 mt = 189 - 193 GeV]...
Thanks to the IR-FP property, the prediction for mt and mH is
stable. ...
Let us consider a simple version of the TMSM with extra
dimensions where the SM gauge group and the third generation of
quarks and leptons are put in D-dimensional bulk, while the first
and second generations live on the 3-brane (4-dimensional
Minkowski space-time).
[ Compare the D4-D5-E6-E7-E8 VoDou
physics model. in which
where 4-dim PST and 4-dim ISS are the products of dimensional
reduction of a high-energy
8-dimensional SpaceTime. ]
The D-dimensions consist of the usual 4- dimensional
Minkowski space-time and extra ... spatial dimensions compactified
at a TeV-scale R^(-1). The number of dimensions D is taken to be
even, D = 6, 8, 10, · · ·, so as to introduce
chiral fermions in the bulk. In order to obtain a 4-dimensional
chiral theory and to forbid massless gauge scalars, we compactify
extra dimensions on the orbifold ... [ T^(D-4) / Z^((D-4)/2)_2
]...
We emphasize that there is no elementary field for Higgs in our
model. The chiral condensation of bulk fermions may generate
dynamically a composite Higgs field, instead.
Hence we investigate RGEs of bulk gauge couplings including
loop effects of the composite Higgs.
We expand bulk fields into KK modes and construct a
4-dimensional effective theory. ...
... We calculate the RGEs by using the UV-BCs ... and determine
mt and mH through the conditions,
- mt = ( v / sqrt(2)) y(mt),
- mH = v sqrt( lambda(mH)) ...
- with v = 246 GeV.
We show results of mt and mH in Fig ... 8 ...
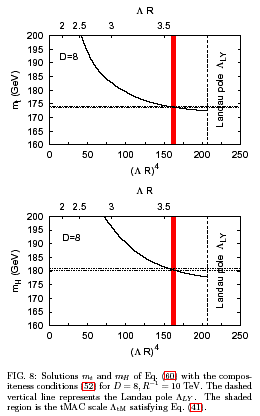
for D = ... 8 ... , R^(-1( = 10 TeV for various values of the
compositeness scale /\. ... the tMAC scale does exist only for D =
8 without much ambiguity, /\_tM R = 3.5-3.6. Identifying /\ with
tM, we depict the region of the tMAC scale for D = 8 by the shaded
area in Fig. 8. ... For D = 8 we predict mt =
172 - 175 GeV, and mH = 176 - 188
GeV, for the range of the compactification scale R^(-1) = 1-100
TeV. The uncertainties ... also include error of alpha_3(MZ) =
0.1172 +/- 0.0020 .
... the prediction ... for mt is consistent with the reality,
the MSbar mass mt = 164.7 +/- 4.9 GeV which is calculated from the
observed value of the pole mass, 174.3 +/-
5.1 GeV . ... our compositeness scale is fixed by the tMAC
scale tM by requiring that the top quark condensation actually
takes place, while other condensations do not. Hence the top mass
as well as the Higgs mass is the prediction in our approach.
...
... the value ... is significantly smaller than that of the
original TMSM in four dimensions which predicted mt >=
200 GeV. Let us consider a simplified
RGE for y neglecting the electroweak gauge interactions ... we
find the quasi IR fixed point y_qIR(mu) ... decreases as ...(D-4)
increases at mu = R^(-1) ... As a result, the prediction of mt
with ...[D-4]... > 0 is substantially lower than that
of the original TMSM with ...D-4]... = 0. ...
The mechanism is still operative even including the electroweak
gauge interactions: In Fig. 10,
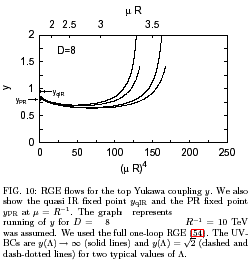
we show the quasi IR fixed point and the behavior of y based on
the full one-loop RGE with various boundary conditions at /\. We
also show the Pendleton-Ross (PR) fixed point ... As far as ... D
= ... 8 ... the value of the PR fixed point is smaller than that
of the quasi IR fixed point ... The top Yukawa coupling at R^(-1)
for D = ... 8 ... is actually between ... the PR fixed point ...
and ... the quasi IR fixed point ... for a sufficiently large top
Yukawa, y)/\_ >= 1 , at high energy scale( /\ R )^(D-4)
.>> 1 ... We note here that the actual prediction of mt with
D = ... 8 is even smaller than the value expected from y_qIR.
We also comment that the predicted values of mt and mH would be
stable thanks to these fixed points, even if the estimate of the
tMAC scale were somewhat changed from ours for some reason. ...
the lower value prediction of mt than that of the original TMSM
can also be understood as follows: Since KK modes of the top quark
(t^(n)) as well as its zero mode (t^(0)) contribute to the VEV v
... the condensate < tbar^(0) t^(0) > is suppressed compared
with the original TMSM and so is the top mass.
Now we discuss implication of our Higgs mass prediction ... The
upper limit of mH from radiative corrections in the SM is mH <
199 GeV at 95% CL . The prediction ... is still below this upper
limit. ...
... SUMMARY AND DISCUSSIONS
We have argued a viable top mode standard model (TMSM) with
TeV-scale extra dimensions where bulk SU(3) x SU(2) x U(1) SM
gauge interactions (without ad hoc four-fermion interactions)
trigger condensate of only the top quark, but not of other quarks
and leptons.
In order for such a situation to be realized, the binding
strength ... should exceed the critical binding strength ... only
for the top quark (tMAC) ... The binding strengths ... were
calculated by using RGEs for bulk SM gauge couplings. ... We then
found that the region of the tMAC scale is squeezed out for D = 6
... while it does exist for D = 8, /\ = (3.5-3.6) R^(-1). We were
not able to draw a reliable conclusion for D = 10 since the MAC
analysis for D = 10 strongly depends on the regularization
scheme.
For D = 8, we predicted the top mass mt and the Higgs mass mH:
mt = 172 - 175 GeV and mH = 176 - 188
GeV, by using RGEs for the top Yukawa and Higgs quartic couplings
with the compositeness conditions at the tMAC scale tM. Our
predictions are governed by the quasi IR-FP and hence are stable
against varying the composite cale. The predicted values would not
be changed so much, even if the region of the tMAC scale got wider
than our estimate for some reason.
Why is the value ...[ of mt ]... significantly smaller
than that of the original TMSM in four dimensions which predicted
mt >= 200 GeV? The value of the
top Yukawa coupling at the quasi IR-FP is ... suppress[ed]
...[by a]... factor 2^(-(D-4)/2) ...[so].. the
mass of the top quark decreases as the number of dimensions
increases. ...
Many issues remain to be explored:
- 1) Our results on the tMAC scale are sensitive to the value
of ... the critical binding strength ... Although we used the
reference value of ... the critical binding strength ... in the
approach of the ladder SD equation neglecting the effect of the
compactification, it would be more preferable if we can
determine ... the critical binding strength ... more reliably.
For such a purpose, we should take into account effects of the
compactification scale R^(-1) which turned out not so small
compared with the tMAC scale /\_tM in our analysis. We also
need running of bulk gauge couplings beyond one-loop
perturbation.
- 2) We incorporated only one composite Higgs doublet into
RGEs, assuming other possible bound states such as
vector/axial-vector bosons are irrelevant. In order to justify
the assumption, we need to solve bound state problems in the
bulk gauge theories. Once such a composite scalar exists, it
should be a tightly bound state formed by strong short distance
dynamics with large anomalous dimension. Such a system is
expected to resemble the gauged Nambu-Jona-Lasinio (GNJL) model
where the compositeness condition is explicitly formulated.
Actually, as it happened in the 4-dimensional case, the pure
gauge dynamics strong at short distance in our case can also
induce strong four-fermion nteractions which may become
relevant operators due to large anomalous dimensions, gamma_m =
D/2 - 1. ...
- 3) There are potential constraints on our model from
precision electroweak measurements. The summation of KK modes
below the cutoff /\ contributes to delta rho as delta rho = (
/\ R )^(D-6) ( M_W R )^2 . In our case with /\ = /\_tM, ( /\_tM
R )^(D-6) = 10 for D = 8, we thus need to take R^(-1) > O(10
TeV), which may be subtle about the fine tuning. ...
- 4) Masses of other quarks and leptons have not been dealt
with in this paper. In the original TMSM, these masses are
descended from the top condensate through ad hoc
flavor-breaking four-fermion interactions. The origin of such
four-fermion interactions will be highly hoped for in the
present scenario.
- 5) Our scenario crucially relies on the short distance
strong dynamics around the composite scale. We thus need a
better-controlled theory in the UV-region. It would be
interesting to study a deconstructed/latticized version of our
model. ...".
Class.
Quantum Grav. 3 (1986) L99-L105, by N. A.
Batakis says:
"... In a standard Kaluza-Klein framework,
M4 x CP2 allows the classical unified description of
an SU(3) gauge field with gravity.
However,
the possibility of an additional SU(2) x U(l) gauge
field structure is uncovered.
... As a result, M4 x CP2 could conceivably accommodate the
classical limit of a fully unified theory for the fundamental
interactions and matter fields. ... [There are]... two
generic possibilities ... for the enlargement of Einstein's
framework, namely
- ... increase the number of spacelike dimensions
...[which]... is mainly exploited in the
...[ordinary]... Kaluza-Klein programme ...[in
which]... the extra dimensions form a vertical 'internal'
compact space of very small ... volume ... and ...
- ... allow the presence of torsion without upsetting the
metricity of connections ...[which involves not
only]... a torsion (totally within M4) ... in the context
of the Einstein-Cartan theory ...[but also]... the ...
mixed components of a torsion in the total space, namely
components which are neither totally vertical nor completely
horizontal. ... such a torsion creates a new and non-trivial
possibility for the accommodation of unified theories in the KK
framework ...[in a]... way in which an
eight-dimensional manifold, locally of the form M4 x CP2, could
... accommodate the classical limit of a fully unified theory
for the fundamental interactions and matter fields ...
...[In]... M4 x CP2 ... the groups G1 and G2 are
SU(3) and SU(2) x U(1), respectively.
The ... G1 [ SU(3) ] ... results from the well known
identification of CP2 with the coset space SU(3)/U(2).
... the G2 ... SU(2) x U(1) ...[has a]...
Killing form is not zero but ... is degenerate, namely (- 1, - 1,
- 1, 0). However, in view of the U(1) factor ... a non-degenerate
metric (- 1, - 1, - 1, - 1) can be (and often is) defined on SU(2)
x U(1). This possibility makes SU(2) x U( 1) a perfectly
acceptable G2 ...The metric is given by ...
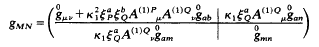
... and the connection 1-form w^M_N is defined as w^M_N =
w^0M_N + K^M_n with w^0M_N the Riemannian connection of the metric
[shown immediately above]... and the contorsion K^M_N
defined ... in terms of the torsion ... T^m_ab = k2 theta^m_I
F^(2)I*_ab where * denotes the M4 dual, k2 is a constant and
theta^m_I is a vielbein ( employed to change the group index I to
the [ CP2 ]... index m ) such that g_mn theta^m_I
theta^n_J = -g_IJ ... The Riemann scalar curvature is then given
by an equation similar to ...
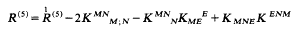 ...
...
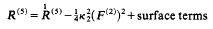 ...
...
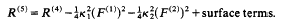
... and the Bianchi identities hold ... The resulting
Einstein-Hilbert action ... when expressed totally within M4 will,
besides gravity (with a cosmological constant), contain the two
gauge fields [SU(3) and SU(2) x U(1)], with the relative
scales between the three parts set by ... constants k1 and k2 as
in ...
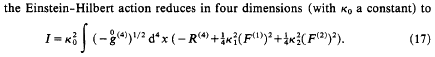
... We recall
- that A(1) [ of SU(3) ] has been introduced at
the level of the metric via the Kaluza ansatz ...[and]
has a role for the coset space ...[CP2]... analogous to
that of the Lorentz (or Poincare) group for ordinary
spacetime,
- while A(2) has been introduced directly through a field
strength F(2) at the level of the connection. In view of the
Bianchi identities for the manifold [ M4 x CP2 ] ...
F(2) will have a well defined and conserved energy-momentum
tensor. However, its gauge group structure is apparently not
mandatory. What our construction has shown is that the geometry
allows a maximal gauge group structure ... The corresponding
[ G2 = SU(2) x U(1) ] gauge symmetry is apparently
unprotected, in contrast to the G1 gauge symmetry.
These results are obviously desirable in view of the ...
association we seek for the two gauge fields with the strong and
electroweak interactions. We also observe that we have exhausted
the generic possibilities for the introduction of interaction
fields into the geometry: besides the metric and a general metric
connection, there is no other independent intrinsic geometric
structure available within our framework. Thus, the following
geometric picture seems to be emerging.
- The gravitational and SU(3) gauge field potentials must be
considered as more fundamental and they completely specify the
metric - essentially they are the metric of M4 x CP2. If no
torsion exists, a symmetric metric connection is uniquely
defined from this metric and M4 x CP2 would then exhibit a
complete left-right symmetry.
- However, ... [ SU(2) x U(1) ] symmetry will break
... with the introduction of torsion. The mixed
[torsion] components of the ...[ SU(2) x U(1)
symmetry.].. will be associated with the spin-1 field F(2)
with a (possibly broken) SU(2) x U(l) gauge symmetry.
- ...[ The torsion ]... components totally within M4
or CP2 could accommodate matter fields in the form of,
respectively, spin density and energy-momentum density
condensates, with mechanisms analogous to those already known
...".
In the paper, Batakis does not discuss "... the introduction of
matter fields ... or related ... issues ...".
With respect to spinor fermions and spin structure, even though
CP2 is not a spin manifold, it is a spin_c (complex) manifold as
described in the book Spin Geometry by Lawson and Michelsohn
(Princeton 1989) particularly page 392.
Also, the book Analysis, Manifolds, and Physics by Choquet-Bruhat
andDeWitt-Morette with Dillard-Bleick (North-Holland 1982 rev ed)
says at page 418:
"... In cases where no spinor structure exists, one may
define a generalized spin structure. In this scheme one makes
topological room for a "spin structure" by mixing in with the
group of a spin bundle an "internal" symmetry group, which is
inextricably involved in the generalized spinor transformation
rule.
It seems to me that the KK model of Batakis may well have a
realistic generalized spin structure, and that if the spinor fermion
spectrum is inherited from the 8-dim Dirac structure of Cl(1,7) prior
to breaking the 8-dim spacetime into MxCP2 at lower energies, then
the Batakis structure may turn out, upon further development, to be
very similar to the D4-D5-E6-E7-E8 VoDou
Physics model (which is in agreement with experiments).
An interesting thing about the 1986 paper of Batakis is that it
provides a constructive counterexample to a well-known paper by
Edward Witten entitled Search for a Realistic Kaluza-Klein Theory,
published in Nuclear Physics B (1981) 412-428, in which Witten
said:
"...seven dimensions is in fact the minimum
dimensionality of a manifold with SU(3)xSU(2)xU(1) symmetry ...
If, therefore, we wish to construct a theory in which
SU(3)xSU(2)xU(1) gauge fields arise as components of the
gravitational field in more than four dimensions, we must have at
least seven extra dimensions. ...".
It is sad that Witten's brilliant understanding of higher
mathematics is accompanied by such a lack of physics intuition.
In a 1983-84 paper
Calculation of Gauge Couplings and Compact Circumferences
from Self-Consistent Dimensional Reduction
by Candelas and Weinberg in Nuclear Physics B237 (1984) 397-441
(reprinted in a book
edited by Applequist, Chodos, and Freund (Addison-Wesley 1987),
Candelas and Weinberg say:
"... we wish to show how fine-structure constants in
general can be calculated in certain theories, in which the gauge
fields arise from the metric of a higher-dimensional space. ...
There are more general (4+N)-dimensional models ... in which N
dimensions form a compact manifold, and a massless gauge field
appears in four dimensions for each Killing vector of this
manifold. A general prescription has ... been given for
calculating the various gauge couplings in such models in terms of
the ratio of 2 pi ( 16 pi G )^(1/2) and various r.m.s.
circumferences. ... In this paper we consider dynamical
compactification ... The (4+N)-dimensional space is again suposed
to break up into a 4-dimensional Minkowski space and a curved
compact N-dimensional manifold, with the curvature governed by
Einstein's field equations. ... the energy-momentum tensor on the
right-hand side on the right-hand side of these equations is ...
supposed to arise ... from the one-loop fluctuations in various
matter fields. ... the energy-momentum tensor is balanced by the
curvature, ans solutions are possible without mass parameters in
the lagrangian, and with the scale of the compact manifold set by
the gravitational constant ... For an N-dimensional compact
manifold whose linear dimensions are of order rho, the one-loop
energy density of f light matter fields is of order f rho^(-4-N) .
The (4+N)-dimensional gravitational constant Gbar is or order G
rho^N , and the Einstein tensor is of order rho^(-2) . Hence ...
rho^2 = G f . The L-loop gravitational corrections to the one-loop
matter energy density ... are less for L >= 2 than the one-loop
matter terms by a factor ... ( 1 / f )^(L-1) . Also, the L-loop
purely gravitational contributions to the energy density ... are
less for L >= 1 than the one-loop matter terms by a factor ...
( 1 / f )^L . ... for f sufficiently large the scale of the
compact manifold is of order sqrt( G f ) ... For manifolds
...[including]... spheres, CPN, and manifolds of simple
groups ... we can normalize the one free parameter rho^2 in the
metric ...
We now make the further assumptions that the matter fields are
massless in 4+N dimensions ... When a (4+N)-dimensional space
breaks up into a 4-dimensional Minkowski space and a compact
manifold, the perturbations of this metric appear in 4 dimensions
in part as a set of massless fields: the Yang-Mills fields
A^mu_a(x) and the gravitations field g_mu nu(x) .
... the classical Einstein-Hilbert action of pure gravity in
4+N dimensions yields in 4 dimensions an action .. where ... F^mu
nu_e are the Yang-Mills curls of those gauge fields A^mu_e that
correspond to closed Killing curves of the compact manifold
...[if there were not many species of matter fields]...
then G_0 could be identified as the Newton gravitational coupling
constant G, and the normalization condition for the Yang-Mills
fields would yield ... g_e = ( 2 pi ( 16 pi G )^(1/2) / N_e s_e )
...[where]... s_e is the r.m.s. circumference of the
manifold along these curves ... However ... assuming ... many
species of matter fields ... radiative corrections generate
induced ... terms ...[involving]... new dimensionless
coefficients ... D_N_e adn E_N ... we see that [for
one-parameter manifolds ... of odd dimensionality]... the true
Newton constant G is given by ( 1 / 16 pi G ) = ( 1 / 16 pi G_0 )
+ ( E_N / rho^2 ) ...
Even a manifold that is stable against all deformations will
become unstable if the temperature is raised above a critical
value T_c ... This suggests that there is a dramatic phase
transition at T = T_c , in which the compactified dimensions
explode outward. One wonders ... whether our universe started with
equal circumferences in all 3+N spatial directions, and became
tightly contracted in N of those dimensions only when the
temperature fell below the critical temperature T_c .
...".
Tony Smith's Home Page Here
is a pdf version of this NJL-BHL-HTYamawaki-CP2KKpage.
......