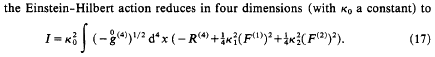- At the Planck scale critical
temperature there is a transition from 8 large dimensions and
4 large dimensions with 4 small compactified CP2 dimensions;
- The spinor fermion particles and antiparticles are not put in
by hand, but are inherited from the high-energy 8-large-dimension
structure so that
- at current experimental energy levels there are 3
generations and
- an inherited subtle
supersymmetry gives ultraviolet finiteness and, along with
Segal Conformal Gravity in
4-dimensional physical spacetime, gives a realistic picture of
the dark energy cosmological "constant" and its relationship to
dark matter and ordinary matter.
A paper of Carlos Castro led me to
consider comparing my D4-D5-E6-E7-E8 VoDou
Physics model with Kaluza-Klein models. Although I have not
worked out the torsion details for the Batakis CP2
model, I am optimistic that it can be worked out in detail and
that the Batakis CP2 model will turn out to be
substantially equivalent to my
D4-D5-E6-E7-E8 VoDou Physics model .
In March 2005, Carlos
Castro has written a paper
which paper deals with geometric techniques that have been used in
calculations of particle masses and force strength constants:
as well as
- by Christian Beck in
Spatio-Temporal Vacuum fluctuations of Quantized Fields (World
Scientific, Singapore 2002 );
- the work of Pierre Noyes in his book Bit-Strings Physics : a
Discrete and Finite Approach to Natural Philosophy , Series in
Knots in Physics, vol. 27 ( Singapore, World Scientific, 2001 )
using Mersenne Primes and
- the work of Matti
Pitkanen using Mersenne
Primes and p-adic numbers.
My understanding of some history of the work of Armand
Wyler is:
- 1970s - Wyler calculates value of 1 / 137.03608 and the
physics community (see Physics Today articles) decides it hates
him and his work;
- 1986-87 - fine structure constant experimentally = 1 /
137.0360 (+/- 1 in last digit) listed in 1987 (3rd) edition of
Introduction to High Energy Physics by Perkins in good agreement
with Wyler's calculation, but there was an Adjustment of the
Fundamental Physical Constants in Rev. Mod. Phys. 59 (1987) 1121
which resulted in a new (as of 1986-87) value of the fine
structure constant as measured by experiment of 1 / 137.0359895
(+/- 61 in last two digits) so that the 1986-87 Adjustment moved
away from Wyler's value;
- 1989-90 - David Gross (armored with the 1986-87
Adjustment) renews in Physics Today attacks on Wyler's work;
- 1998 - a new Adjustment (called the 1998 recommended
values) is made, giving value of the fine structure constant as
measured by experiment of 1 / 137.03599976 (+/- 50 in last two
digits)
- 2001 - March 2001 issue of Physics Today has an article
by Mohr and Taylor entitled Adjusting the Values of the
Fundamental Constants (pages 29-34), which article says in part:
"... the numbers form a tightly linked set - very few of the
values are independent of the others. ... For example ... Now the
electron charge is determined indirectly from other constants. ...
The basic approach to finding a self-consistent set of values of
these constants is to identify the critical experiments, determine
the theoretical expressions as functions of the fundamental
constants that make predictions for the measured quantities, and
adjust the values of the constants to achieve the best match
between theory and experiment. ...".
The values of the fine structure constant etc that you see on the
web site of the Particle Data Group are only ONE POSSIBLE
"self-consistent set of values" which set was obtained by
"adjust[ing] ... to achieve the best match". It is in my
opinion not only possible, but likely, that the 1986-87 Adjustments
were adjusted to achieve a mismatch between the value of the fine
structure constant and Wyler's hated-by-the-physics-community
calculations and that there very likely exists even at the present
time another "self-consistent set of values" containing a fine
structure constant value that is in good agreement with Wyler's
calculations. I note that individuals (including me) do not have
sufficient time and resources to construct in detail such a
"self-consistent set of values", and it is obvious that the physics
establishment would be quite hostile to expending money, time, and
effort in a project to study the total landscape of possible
"self-consistent set[s] of values". My point here is that you
should in my opinion not take too seriously any disagreement between
the current consensus value of the fine structure constant and
Wyler's calculations. Nature is NOT governed by the rule of the
majority of voting humans, and a human consensus is NOT always
right.
Also, the stated error bars in the current recommended values of
the fine structure constant are (in my opinion) probably grossly
wrong and subject to serious misinterpretation. For instance:
1 / Wyler's value = 137.03608
1 / 1998 Adjusted recommended experimental value =
= 137.03599976 (+/- 50 in last two digits)
Difference = 137.03608 - 137.03600 (rounded) = 0.00008
Error bar = = 0.0000005
Number of error bars in difference = 800 / 5 = 160
could be misinterpreted as showing that Wyler's value (which is
also my calculated value) is wrong by 160 standard deviations, and
therefore clearly ruled out by experiment.
However, in my opinion (even disregarding the possibility of
rigging the 1986-87 and subsequent adjustments of physical "constant"
values to disagree with Wyler, such a way of thinking is just an
illustration of the progression, in increasing order of badness: Lies
- Damn Lies - Statistics. I think that this is one of many instances
in which stated physics error bars used are ridiculously
unrealistic.
In his paper described above, Carlos
Castro says, in part [ I have extensively modified
it by editing out the parts of it with which I disagree, which
changes are substantial, so any errors you see in reading this edited
version are probably my fault. For example, I have omitted Carlos
Castro's use of a factor 2V(S2) which he used as volumes of
light-cone boundaries at past and future infinities with respect to
virtual emission/absorption of gauge boson force carriers ( I
think that all such bosons MUST come from past infinity and go to
future infinity, so that any factor should be 1x1 = 1 = unity, and
not anything involving 2V(S2).) Therefore, what you see here may
NOT be what Carlos Castro thinks, and he should not be blamed for any
errors that my editing has created. That having been said, I
also want to say that overall I think that Carlos Castro's paper is
brilliant, and I especially like his idea linking the Wyler-type
models to generalized Kaluza-Klein models
such as described by Batakis. I have designated material
that I omitted by ... and have enclosed my additions in [ ]
. ] :
"... Geometric Probability ... is the study of the
probabilities involved in geometric problems, e.g., the
distributions of length, area, volume, etc. for geometric objects
under stated conditions. One of the most famous problem is the
Buffon's Needle Problem of finding the probability that a needle
of length l will land on a line, given a floor with equally spaced
parallel lines a distance d apart. ... the Geometric Probability
is essentially the ratio of the areas of a rectangle of length 2d,
and width l and the area of a circle of radius d . For l > d,
the solution is slightly more complicated. ... The Buffon needle
problem provides with a numerical experiment that determines the
value of pi empirically. Geometric Probability is a vast field
with profound connections to Stochastic Geometry.
Feynman long ago speculated that the fine structure constant
may be related to pi . This is the case as Wyler found long ago
[1960s-70s]... We will based our derivation of the fine
structure constant based on Feynman's physical interpretation of
the electron's charge as the probability amplitude that an
electron emits (or absorbs) a photon. The clue to evaluate this
probability within the context of Geometric Probability theory is
provided by the electron self-energy diagram. Using Feynman's
rules, the self-energy (p) as a function of the electron's
incoming ( outgoing ) energy-momentum p mu is given by
...[an]... integral involving the photon and electron
propagator along the internal lines ... The integral is taken with
respect to the values of the photon's energy-momentum k mu ... one
can see that the electron self-energy is proportional to the
fine structure constant alpha_EM = e^2, the square of the
probability amplitude ( in natural units of hbar = c = 1 ) and
physically represents the electron's emission of a virtual
photon ( off-shell ...) of energy-momentum k at a given moment,
followed by an absorption of this virtual photon at a later
moment.
Based on this physical picture of the electron self-energy
graph, we will evaluate the Geometric Probability that ...[
a particle]... emits a ...[gauge boson]... at ... (
infinite past ) and re-absorbs it at a much later time ... (
infinite future). The off-shell ( virtual ) ...[gauge
boson]... associated with the ...[particle]...
self-energy diagram ... can remain off-shell ... k^2 =/= 0
....[all the time]... between the moments of emission and
absorption by the ...[particle]...[as it moves
along its path in the]... conformally compactified real
Minkowski spacetime Q4 = Mbar4 = S3 x S1/Z2 = S3 x RP1
...[which has]... precisely the same as the topology of
the Shilov boundary Q4 of the 4 complex-dimensional ... [ D4 =
Spin(4, 2) / Spin(4) x U(1) = SU(2,2) / S(U(2)xU(2))
]...
[Shilov boundaries often describe the physically
relevant part of larger domains, as in the case in which
compactified Minkowski spacetime is the Shilov boundary Q4 of
the complex domain D4.] ... the ( Shilov ) boundaries are
essential mathematical features to understand the geometric
derivation of all the coupling constants. ... we will recur to
Penrose's ideas ... of conformal compactifications of Minkowski
spacetime ... The conformal group [ Spin(4,2) = SU(2,2)
] leaves the light-cone ...[invariant]... and ...
does not alter the causal properties of spacetime ... The
action of the discrete group Z2 [in Q4 = S3 x S1/Z2]
amounts to an antipodal identification of ... the past timelike
infinity ... with the future timelike infinity ...
Shilov boundaries of homogeneous (symmetric spaces) complex
domains, G/K ... are not the same as the ordinary topological
boundaries (except in some special cases). ... Shilov
boundaries are the minimal subspaces of the ordinary
topological boundaries ...[for which]... the
holomorphic data in the interior ( bulk ) of the domain is
fully determined by the holomorphic data on the Shilov
boundary. The latter has the property that the maximum modulus
of any holomorphic function defined on a domain is attained at
the Shilov boundary.
... The action of the discrete group Z2 amounts to an antipodal
identification of t\... the past timelike infinity ... with the
future timelike infinity ... ... D4 of 4 complex dimensions is
an 8 real-dim Hyperboloid of constant negative scalar curvature
that can be identified with the conformal relativistic curved
phase space associated with the electron (a particle ) moving in a
4D Anti de Sitter space AdS4. [It]... is a Hermitian
symmetric homogeneous coset space associated with the 4D conformal
group SO(4, 2) since D4 = SO(4, 2) / SO(4)xSO(2). ...
[ The most basic force is gravity, which holds space-time
together by emitting/absorbing virtual gravitons with probability
1. In that sense, the Geometric Probability strength of
gravity is the strongest of any of the four forces, and should be
the denominator in the ratio describing the fundamental strength
of each force. Therefore, the first calculation should be of
the Geometric Probability strength of gravity. ]
... the MacDowell-Mansouri-Chamseddine-West formulation of
Gravity [is] based on the ...[anti-deSitter]...
group SO(3, 2) which has the same number of 10 generators as
the 4D Poincare group. ...
[Since the largest local isotropy group of]... D4 =
SO(4, 2) / SO(4)xSO(2) ...[is SO(4), and since the Euclidean
version of the Anti de Sitter Group is SO(5), neither D4 nor its
Shilov boundary] ... space Q4 = S3 x RP1 is ... large enough
to implement the action of ... the Anti de Sitter Group SO(3, 2)
[that]... is required in the
MacDowell-Mansouri-Chamseddine-West formulation of Gravity.
...
[A sufficiently large space with SO(5) local isotropy
group is]... 5 complex-dimensional ... D5 = SO(5, 2) / SO(5)x
SO(2) ... the 10 real-dim Hyperboloid ... corresponding to the
conformal relativistic curved phase space of a particle moving in
5D Anti de Sitter Space AdS5 ...
[Its Shilov boundary]... space Q5 = S4 x RP1 is
large enough to implement the action of SO(5) via the ... space S4
= SO(5)/SO(4). This justifies the embedding procedure of D4 ->
D5 ... and Q4 -> Q5 ...
Hence, the Geometric Probability ratio [for the force
strength of gravity] becomes ...[ proportional to the
measure mu[Q4] of the entire compactified Minkowski Mbar4
through which the virtual graviton can propagate, and inversely
proportional to the measure mubar[Q4] of Q4 as embedded in
Q5, so that
GeomStrength_gravity = mu[Q4] /
mubar[Q4]
and in terms of the larger embedding Shilov boundary Q5, using
the embedding-adjustment space S4 = SO(5)/SO(4), we have
GeomStrength_gravity = mu[Q4] / mubar[Q4]
= V(S4) mu[Q5] / mu_N[Q5]
The]... standard normalized measure mu_N[Q5]
[is] based on the Poisson kernel and involv[es] a
normalization factor of 1/V(Q5) [and] is not invariant
under the full group SO(5, 2) . It is only invariant under the
isotropy group of the origin SO(5)xSO(2). In order to construct an
invariant measure on Q5 under the full group SO(5, 2) one requires
to introduce a crucial factor related to the Jacobian measure
involving the action of the conformal group SO(5, 2) on the full
bulk domain D5. ...[so]... we turn to the Hermitian metric
on D5 constructed by Hua ... which is SO(5, 2)-invariant and is
based on the Bergmann kernel ... involving a crucial normalization
factor of 1/V D5).
As explained by ...[ G. Gonzalez-Martin ]... one has
:
mu_N[Q5] / mu[Q5] = ( 1 / V(Q5) ) ( 1 /
||Jac_C|| ) = ( 1 / V(Q5) ) sqrt( 1 / ||Jac_C(Jac_C*)|| ) = ( 1 /
V(Q5) ) sqrt( 1 / ||Jac_R|| ) = ( 1 / V(Q5) ) sqrt( 1 / sqrt( |
det(g) | ) = ( 1 / V(Q5) ) ( | det(g) |^(-(1/4)) ) =
V(D5)^(1/4) / V(Q5)
... the z dependence of the complex Jacobian is no longer
explicit because the determinant of the SO(5, 2) matrices is
unity. This explains very clearly the origins of the factor [
V (D5) ]^(1/4) in Wyler's formula for the fine structure
constant ... This reduction factor of V (Q5) is in this case given
by V (D5)1/4. As we shall see below, the power of 1/4 is related
to the inverse of the dim(S4) = 4. This summarizes, briefly, the
role of Bergmann kernel ... in the construction by Hua ... and
adopted by Wyler ... of the Hermitian metric of a bounded
homogenous ( symmetric ) complex domain. To sum up, we must
perform the reduction from V (Q5) -> V (Q5) / V (D5)^(1/4) in
the construction of the normalized measure mu_N[Q5] .
[ Comment by Tony Smith - With respect to the factor
V(D5)^(1/4), I think that with the Jacobian language used by
Gonzalez-Martin to get the factor V(D5)^1/4 is substantially
equivalent to my statement about
my model "... Vol(Dforce)^( 1
/ mforce ) stands for a dimensional normalization factor (to
reconcile the dimensionality of the Internal Symmetry Space of the
target vertex with the dimensionality of the link from the origin
to the target vertex) ..." and to Smilga's
statement about his model"... If we integrate over Dbar5 using
this new parameter set, each si will be responsible for a
contribution of V(D5)^(1/4) to the volume of Dbar5. Three of these
parameters can be mapped onto the transferred momentum q. The
fourth parameter s4 ... corresponds to a momentum transfer within
each of the particle momenta, without any momentum transfer
between the particles. such transitionscontribute to the volume of
C5. We can perform the integration over s4 and obtain a correcting
factor to the aready calculated volume V(C5) of V(D5)^(1/4).
...".
Taking the V(D5)^(1/4) factor into account, we have
GeomStrength_gravity = mu[Q4] /
mubar[Q4] = V(S4) mu[Q5] / mu_N[Q5] =
= V(S4) V(Q5) / V(D5)^(1/4)
where the volumes are ]...
- V(D5) = pi^5 / ( 2^4 x 5! )
- V(Q5) = 8 pi^3 / 3
- V(S4) = 8 pi^2 / 3
[ Define all the force strengths in terms of
GeomStrength_G, the geometric force strength of gravity, which is
the strongest of all geometric force strengths. Therefore,
alpha_G = GeomStrength_gravity /
GeomStrength_gravity = 1
and, for the other forces we have alpha_force =
GeomStrength_force /GeomStrength_gravity
...[ For alpha_C, the color force strength, use...
the internal symmetry space ... CP2 = SU(3) / U(2) = SU(3) /
SU(2) x U(1) ... associated with the SU(3) color group ... the
volume V (CP2) = V (S4) = 8 pi^2 / 3 ... V(S5) = 4 pi^3 ... V(B6)
= pi^3 /6 ... we have
alpha_C = ( V(CP2) V(S5) / V(B6)^(1/4) ) /
GeomStrength_gravity = 0.6286
]... that [value] corresponds to the strong
coupling constant at an energy related to the pion masses ... 241
MeV ...[ As Batakis says in his paper about
CP2 Kaluza-Klein, "... [ Color SU(3) ] has been
introduced at the level of the metric via the Kaluza ansatz
...[and] has a role for the coset space
...[CP2]... analogous to that of the Lorentz (or Poincare)
group for ordinary spacetime ...". ]...
...[ For alpha_W, the weak force strength, use ... the
CP1 = S2 subspace of the internal symmetry space CP2, since the
weak force SU(2) acts globally on S2 = CP1 = SU(2) / U(1) =
Spin(3) / Spin(2)
Since it takes two copies of S2 to cover all 4 dimensions of
covariant polarization for weak bosons, and since the Shilov
boundary of the interior of S2xS2 is S2 + S2 (two copies of S2)
... V(S2) = 4 pi ... V(Q3) = 4 pi^2 ... V(D3) = pi^3 / 24 ... we
have
alpha_W = ( 2V(S2) V(Q3) / V(D3)^(1/2) ) /
GeomStrength_gravity = 0.2536
]... that [value] corresponds to the weak geometric
coupling constant alpha_W at an energy of the order of ... 146 GeV
... the Fermi coupling GFermi ....[in terms of the proton mass
is about]... 1.04 x 10^(-5) ... [ As Batakis
says in his paper about CP2 Kaluza-Klein, "... [ SU(2) x
U(1) ] symmetry will break ... with the introduction of
torsion. The mixed [torsion] components of the ...[
SU(2) x U(1) symmetry.].. will be associated with the spin-1
field ... with a (possibly broken) SU(2) x U(l) gauge symmetry.
...". ]...
...[ For alpha_E, the electromagnetic force strength,
use ... an S1 subspace of the internal symmetry space CP2 = C2 u
CP1 = C2 u S2 located in the C2 independent of the weak force S2 =
CP1, since the electromagnetic force U(1) acts globally on S1 =
U(1) . Note that for each of the two S2 placement choices
described for alpha_W, there are two C s in the C2 = CxC part of
CP2 = C2 u S2, and each of those C s contains a natural S1 , so
that in all there are 4 S1 placement choices for alpha_E.
Since it takes four copies of S1 to cover all 4 dimensions of
covariant polarization for electromagnetic photons, and since the
Shilov boundary of the interior of S1xS1xS1xS1 = T4 is S1 + S1 +
S1 + S1 (four copies of S1) ... V(S1) = 2 pi ... V(Q2) = 2 pi / 2
since Q2 = RP1 = S1/Z2 ... V(D2) = pi since D2 is a circle of
radius 1 whose circumference is S1 only half of which
circumference is Q2 ... we have
alpha_E = ( 4 V(S1) V(Q2) / V(D2)^(1/1) ) /
GeomStrength_gravity = 1 / 137.03608
]... that [value] corresponds to ... the scale of
the Bohr radius ... The Bohr radius is associated with the ground
( most stable ) state of the Hydrogen atom ... The spectrum
generating group of the Hydrogen atom is well known to be the
conformal group SO(4, 2) due to the fact that there are two
conserved vectors, the angular momentum and the Runge-Lentz
vector. After quantization, one has two commuting SU(2) copies
SO(4) = SU(2)xSU(2). Thus, it makes physical sense why the
Bohr-scale should appear in this construction. ... The Bohr radius
corresponds to an energy of 137.036 x 2 x 13.6 eV = 3.72 x 10^3 eV
. It is well known that the Rydberg scale, the Bohr radius, the
Compton wavelength of electron, and the classical electron radius
are all related to each other by a successive scaling in products
of EM. ... [ As Batakis says in his paper
about CP2 Kaluza-Klein, "... [ SU(2) x U(1) ] symmetry
will break ... with the introduction of torsion. The mixed
[torsion] components of the ...[ SU(2) x U(1)
symmetry.].. will be associated with the spin-1 field ... with
a (possibly broken) SU(2) x U(l) gauge symmetry. ...".
]...
Concluding, the Geometric Probability that an electron emits a
photon ... and absorbs it ... is given by the ratio of the ratios
of measures, and it agrees with Wheeler's ideas that one must
normalize the couplings with respect to the geometric coupling
strength of Gravity ...
In his paper
Class.
Quantum Grav. 3 (1986) L99-L105, N. A.
Batakis says:
"... In a standard Kaluza-Klein framework,
M4 x CP2 allows the classical unified description of
an SU(3) gauge field with gravity.
However,
the possibility of an additional SU(2) x U(l) gauge
field structure is uncovered.
... As a result, M4 x CP2 could conceivably accommodate the
classical limit of a fully unified theory for the fundamental
interactions and matter fields. ... [There are]... two
generic possibilities ... for the enlargement of Einstein's
framework, namely
- ... increase the number of spacelike dimensions
...[which]... is mainly exploited in the
...[ordinary]... Kaluza-Klein programme ...[in
which]... the extra dimensions form a vertical 'internal'
compact space of very small ... volume ... and ...
- ... allow the presence of torsion without upsetting the
metricity of connections ...[which involves not
only]... a torsion (totally within M4) ... in the context
of the Einstein-Cartan theory ...[but also]... the ...
mixed components of a torsion in the total space, namely
components which are neither totally vertical nor completely
horizontal. ... such a torsion creates a new and non-trivial
possibility for the accommodation of unified theories in the KK
framework ...[in a]... way in which an
eight-dimensional manifold, locally of the form M4 x CP2, could
... accommodate the classical limit of a fully unified theory
for the fundamental interactions and matter fields ...
...[In]... M4 x CP2 ... the groups G1 and G2 are
SU(3) and SU(2) x U(1), respectively.
The ... G1 [ SU(3) ] ... results from the well known
identification of CP2 with the coset space SU(3)/U(2).
... the G2 ... SU(2) x U(1) ...[has a]...
Killing form is not zero but ... is degenerate, namely (- 1, - 1,
- 1, 0). However, in view of the U(1) factor ... a non-degenerate
metric (- 1, - 1, - 1, - 1) can be (and often is) defined on SU(2)
x U(1). This possibility makes SU(2) x U( 1) a perfectly
acceptable G2 ...The metric is given by ...
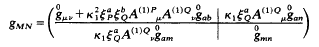
... and the connection 1-form w^M_N is defined as w^M_N =
w^0M_N + K^M_n with w^0M_N the Riemannian connection of the metric
[shown immediately above]... and the contorsion K^M_N
defined ... in terms of the torsion ... T^m_ab = k2 theta^m_I
F^(2)I*_ab where * denotes the M4 dual, k2 is a constant and
theta^m_I is a vielbein ( employed to change the group index I to
the [ CP2 ]... index m ) such that g_mn theta^m_I
theta^n_J = -g_IJ ... The Riemann scalar curvature is then given
by an equation similar to ...
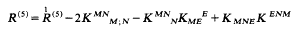 ...
...
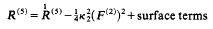 ...
...
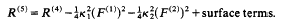
... and the Bianchi identities hold ... The resulting
Einstein-Hilbert action ... when expressed totally within M4 will,
besides gravity (with a cosmological constant), contain the two
gauge fields [SU(3) and SU(2) x U(1)], with the relative
scales between the three parts set by ... constants k1 and k2 as
in ...
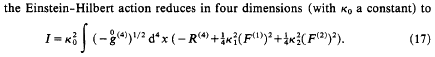
... We recall
- that A(1) [ of SU(3) ] has been introduced at
the level of the metric via the Kaluza ansatz ...[and]
has a role for the coset space ...[CP2]... analogous to
that of the Lorentz (or Poincare) group for ordinary
spacetime,
- while A(2) has been introduced directly through a field
strength F(2) at the level of the connection. In view of the
Bianchi identities for the manifold [ M4 x CP2 ] ...
F(2) will have a well defined and conserved energy-momentum
tensor. However, its gauge group structure is apparently not
mandatory. What our construction has shown is that the geometry
allows a maximal gauge group structure ... The corresponding
[ G2 = SU(2) x U(1) ] gauge symmetry is apparently
unprotected, in contrast to the G1 gauge symmetry.
These results are obviously desirable in view of the ...
association we seek for the two gauge fields with the strong and
electroweak interactions. We also observe that we have exhausted
the generic possibilities for the introduction of interaction
fields into the geometry: besides the metric and a general metric
connection, there is no other independent intrinsic geometric
structure available within our framework. Thus, the following
geometric picture seems to be emerging.
An interesting thing about the 1986 paper of Batakis is that it
provides a constructive counterexample to a well-known paper by
Edward Witten entitled Search for a Realistic Kaluza-Klein Theory,
published in Nuclear Physics B (1981) 412-428, in which Witten
said:
"...seven dimensions is in fact the minimum
dimensionality of a manifold with SU(3)xSU(2)xU(1) symmetry ...
If, therefore, we wish to construct a theory in which
SU(3)xSU(2)xU(1) gauge fields arise as components of the
gravitational field in more than four dimensions, we must have at
least seven extra dimensions. ...".
It is sad that Witten's brilliant understanding of higher
mathematics is accompanied by such a lack of physics intuition.
In a 1983-84 paper
Calculation of Gauge Couplings and Compact Circumferences
from Self-Consistent Dimensional Reduction
by Candelas and Weinberg in Nuclear Physics B237 (1984) 397-441
(reprinted in a book
edited by Applequist, Chodos, and Freund (Addison-Wesley 1987),
Candelas and Weinberg say:
"... we wish to show how fine-structure constants in
general can be calculated in certain theories, in which the gauge
fields arise from the metric of a higher-dimensional space. ...
There are more general (4+N)-dimensional models ... in which N
dimensions form a compact manifold, and a massless gauge field
appears in four dimensions for each Killing vector of this
manifold. A general prescription has ... been given for
calculating the various gauge couplings in such models in terms of
the ratio of 2 pi ( 16 pi G )^(1/2) and various r.m.s.
circumferences. ... In this paper we consider dynamical
compactification ... The (4+N)-dimensional space is again suposed
to break up into a 4-dimensional Minkowski space and a curved
compact N-dimensional manifold, with the curvature governed by
Einstein's field equations. ... the energy-momentum tensor on the
right-hand side on the right-hand side of these equations is ...
supposed to arise ... from the one-loop fluctuations in various
matter fields. ... the energy-momentum tensor is balanced by the
curvature, ans solutions are possible without mass parameters in
the lagrangian, and with the scale of the compact manifold set by
the gravitational constant ... For an N-dimensional compact
manifold whose linear dimensions are of order rho, the one-loop
energy density of f light matter fields is of order f rho^(-4-N) .
The (4+N)-dimensional gravitational constant Gbar is or order G
rho^N , and the Einstein tensor is of order rho^(-2) . Hence ...
rho^2 = G f . The L-loop gravitational corrections to the one-loop
matter energy density ... are less for L >= 2 than the one-loop
matter terms by a factor ... ( 1 / f )^(L-1) . Also, the L-loop
purely gravitational contributions to the energy density ... are
less for L >= 1 than the one-loop matter terms by a factor ...
( 1 / f )^L . ... for f sufficiently large the scale of the
compact manifold is of order sqrt( G f ) ... For manifolds
...[including]... spheres, CPN, and manifolds of simple
groups ... we can normalize the one free parameter rho^2 in the
metric ...
We now make the further assumptions that the matter fields are
massless in 4+N dimensions ... When a (4+N)-dimensional space
breaks up into a 4-dimensional Minkowski space and a compact
manifold, the perturbations of this metric appear in 4 dimensions
in part as a set of massless fields: the Yang-Mills fields
A^mu_a(x) and the gravitations field g_mu nu(x) .
... the classical Einstein-Hilbert action of pure gravity in
4+N dimensions yields in 4 dimensions an action .. where ... F^mu
nu_e are the Yang-Mills curls of those gauge fields A^mu_e that
correspond to closed Killing curves of the compact manifold
...[if there were not many species of matter fields]...
then G_0 could be identified as the Newton gravitational coupling
constant G, and the normalization condition for the Yang-Mills
fields would yield ... g_e = ( 2 pi ( 16 pi G )^(1/2) / N_e s_e )
...[where]... s_e is the r.m.s. circumference of the
manifold along these curves ... However ... assuming ... many
species of matter fields ... radiative corrections generate
induced ... terms ...[involving]... new dimensionless
coefficients ... D_N_e adn E_N ... we see that [for
one-parameter manifolds ... of odd dimensionality]... the true
Newton constant G is given by ( 1 / 16 pi G ) = ( 1 / 16 pi G_0 )
+ ( E_N / rho^2 ) ...
Even a manifold that is stable against all deformations will
become unstable if the temperature is raised above a critical
value T_c ... This suggests that there is a dramatic phase
transition at T = T_c , in which the compactified dimensions
explode outward. One wonders ... whether our universe started with
equal circumferences in all 3+N spatial directions, and became
tightly contracted in N of those dimensions only when the
temperature fell below the critical temperature T_c .
...".
Tony's Home Page ------------------------
Here is a pdf version of this KaluzaKlein
page.
![]() ...
...![]()