Tony Smith's Home Page | FRAMES
VERSION OF THIS PAGE |
My D4-D5-E6-E7-E8 VoDou
Physics Model meets Einstein's
Criterion:
"... a theorem which at present can not
be based upon anything more than upon a faith in the simplicity,
i.e., intelligibility, of nature: there are no arbitrary
constants ... that is to say, nature is so constituted that it is
possible logically to lay down such strongly determined laws that
within these laws only rationally completely determined constants
occur (not constants, therefore, whose numerical value could be
changed without destroying the theory). ...".
Here is an Introduction to VoDou
Physics.
Here are SESAPS 2002 and a
December 2001 overview of D4-D5-E6-E7-E8 VoDou Physics and Fermion
Masses, including Quark Masses and the Proton/Electron Mass
Ratio.
The Truth Quark, through its strong
interaction with Higgs Vacua, may have two excited energy levels at
225 GeV and 173 GeV, above a ground state at 130 GeV. The 173
GeV excited state may exist due to appearance of a Planck-energy
vaccum with < phi_vac2 > = 10^19 GeV in addition to the
low-energy Standard Model vacuum with < phi_vac1 > = 252
GeV.
Here are 26-dim Strings as
Quantum Theory, 27-dim M-theory of Timelike Brane-Universes, and
28-dim F-theory of Spacelike Brane-Universes.
My D4-D5-E6-E7-E8 VoDou Physics model is based on Clifford algebras.
Here is a brief rough outline of how it works
(ignoring subtleties such as signature etc):
Consider any arbitrary real Clifford algebra Cl(N),
where N is the (arbitrary) dimension of the vector space.
No matter how large is N
(by going to a larger N, you can assume that N is divisble by 8)
it can, by the periodicity theorem, be factored into the tensor product
Cl(N) = Cl(8) x...( N/8 times )...x Cl(8)
which is the basis for construction of
a real hyperfinite II1 von Neumann algebra factor.
Therefore,
I use Cl(8) as building blocks of the physics model.
Since Cl(8) has the structure of the VoDou divination method IFA,
I call the model VoDou Physics.
Cl(8) is 2^8 = 16x16 = 256-dimensional, and has graded structure
1 8 28 56 70 56 28 8 1
The first 8 is the vector space;
the first 28 is the bivector Spin(8) Lie algebra;
the spinors are 16-dimensional,
and break down into two mirror-image 8-dim half-spinors.
These things fit together in a natural way
to form a Lagrangian over 8-dim spacetime:
Integral over vector space of bivector/covariant derivative term
and spinor/Dirac operator term
Note that all these parts, including the spinors and Dirac operator,
are natural parts of the Clifford algebra and are NOT ad hoc
additions-put-in-by-hand.
The 8-dim spacetime breaks down into
4-dim Physical SpaceTime that looks topologically like S1 x S3
plus
4-dim Internal Symmetry Space that looks topologically like CP2.
The CP2 = SU(3) / U(2) is a representation space on
which the color SU(3) acts globally
and the electroweak U(2) = SU(2)xU(1) acts locally.
S1 x S3 Physical SpaceTime is
the Shilov boundary of the bounded domain corresponding to
the symmetric space Spin(2,4)/Spin(1,3)xU(1) = SU(2,2) / SU(2)xU(2)
which has 8 real dimensions and 4 complex dimensions.
Its the symmetry is that
of the 15-dim conformal group Spin(2,4) = SU(2,2)
and you get Gravity and the Higgs mechanism
by gauging the conformal group as
described by Mohapatra in section 14.6 of his book
Unification and Supersymmetry (2nd edition, Springer-Verlag 1992).
The 28 generators of Spin(8),
after dimensional reduction of spacetime, are transformed into:
16 generators of U(2,2) = Spin(2,4)xU(1) where Spin(2,4) is
the conformal group that gives Gravity, the Higgs mechanism,
and a comlex phase for particle propagators.
12 generators of SU(3)xSU(2)xU(1) for the Standard Model,
whose global group structure is discussed here.
The gauge boson process is described in more detail on this web page.
More about the Clifford structure,
including position-momentum duality, is HERE.
The most important calculation in my model, in my opinion,
is my calculation of the Truth quark mass prior to its discovery at Fermilab,
so that calculation of 130 GeV is in fact a prediction.
Fermilab analyses of the data state
that the Truth quark mass is about 170 GeV,
but
I think that their analyses are wrong and that a correct
analysis of the same data is consistent with
a Truth quark mass of about 130 GeV as my model predicted.
Details of my comparison of the data analyses are on
this web page and others to which it is linked.
A version of that material is on the e-print archive
as physics/0006041.
As to the calculations themselves,
they are based on the D4-D5-E6-E7-E8 VoDou Physics model,
which is based on Clifford algebras, symmetric spaces,
and Shilov boundaries of bounded complex homogeneous domains.
A summary of my calculations is on this web page.
More explicit details of the Truth quark mass,
and other quark and lepton mass calculations, are on this web page.
Here is a more visual outline of the Clifford
Algebra Foundation of VoDou
Physics:
Cl(8N) = 2^(8N) =
= Cl(8) x ...Ntimes... x Cl(8) = (2^8)^N
2^8 = 256 = 16 x 16 = 1 8 28 56 70 56 28 8 1
4 16 = U(2,2) = Spin(2,4) x U(1)
*-* (8) + (8)
4 12 = SU(3) x SU(2) x U(1)
*-* or *-* (8,8) + (8,8)
*-* (8,8,8) + (8,8,8)
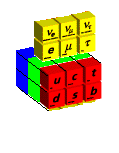
 D4 D5 E6 E7
Spin(8) Spin(10)
28 8 (+1+8) 16 (+1+16) 27 (+1+27)
Generation-1
Gravity SpaceTime Fermions
16-U(4) 4 8 MacroSpace
Generation-1 of
Standard Model Internal Space AntiFermions Many-Worlds
12-SU(3)xSU(2)xU(1) 4 8
D4 D5 E6 E7
Spin(8) Spin(10)
28 8 (+1+8) 16 (+1+16) 27 (+1+27)
Generation-1
Gravity SpaceTime Fermions
16-U(4) 4 8 MacroSpace
Generation-1 of
Standard Model Internal Space AntiFermions Many-Worlds
12-SU(3)xSU(2)xU(1) 4 8
(The Lepton-Quark image to the above left is
adapted from a
Fermilab web page.)
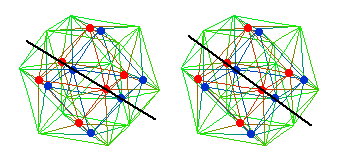
The 24-cell shown above represents
the 24 root vector gauge bosons of the 28-dimensional Spin(8) gauge
group. The dual 24-cell
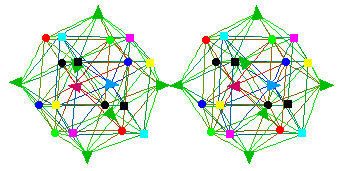
represents:

Together, the 24-cell plus its dual
24-cell correspond to the 48 root vector vertices of the
52-dimensional exceptional Lie algebra F4., and F4
can be thought of as the Real Part of the 52+26 = 78-dimensional Lie
algebra E6 of the D4-D5-E6-E7-E8 VoDou Physics model.
Since my D4-D5-E6-E7-E8 Physics
Model is based on the Cl(8)
Clifford Algebra that is related to the
16x16 = 256 Odu of IFA, I think that my
physics model is really in fact VoDou
Physics, so I sometimes call it that.

I learned about Clifford Algebras from
studying under David
Finkelstein at Georgia Tech since around 1981. Both David
Finkelstein and I use the the Periodicity-8
tensor product Cl(N) = Cl(8) x
...N/8 times... x Cl(8)) in our physics models. With respect to
his model, David
Finkelstein says "... An assembly with Clifford statistics we call a
squad. The Spinorial Chessboard shows how the dynamics, a large squad
of chronons, can spontaneously break down into a Maxwellian assembly
of squads of 8 chronons each. Squads of 8 are special this way.
...". Also, see, for example, the
paper hep-th/0009086, Clifford Algebra as Quantum Language, by James
Baugh, David Ritz Finkelstein, Andrei Galiautdinov, and Heinrich
Saller, and the paper by D. Finkelstein and E. Rodriguez, The
quantum pentacle, International Journal of Theoretical Physics 23,
887-894 (1984).
Here is the introduction to my May 2002
Cookeville Clifford Algebra talk.
In Phys. Lett. 149B (1984) 117, Green amd Schwarz showed superstring
theory to be anomaly-free. Richard
Feynman said, in Davies and Brown, Superstrings, Cambridge
1988, pp. 194-195):
"... I do feel strongly that this is nonsense! ... I think
all this superstring stuff is
crazy and is in the wrong direction. ... I don't like it that they're
not calculating anything. ... why are the
masses of the various particles such as quarks what they
are? All these numbers ... have no explanations in these
string theories - absolutely none! ... "
I have agreed with Feynman's opinion about superstrings as a model
of physics of particles and forces in 4-dimensional spacetime since
1984, when I began to construct a TOE
(Theory Of Everything) physics model, the D4-D5-E6-E7-E8 Physics
Model, in which I can calculate particle
masses and force strengths, including the
The model can be formulated as a Feynman
Checkerboard on a discrete HyperDiamond
lattice spacetime with a Many-Worlds
Quantum Theory.
The Geometry of the Super
Implicate Order, or MacroSpace,
can be described at the Nearest Neighbor level by the 27-complex-dimensional
symmetric space E7 / E6xU(1), where String
Theory in a 26-dimensional subspace can be used to describe
Sarfatti Back-Reaction and Quantum
Consciousness.
I sometimes use some other names for my
VoDou
Physics model:
The Planck length is the fundamental lattice link scale in
the D4-D5-E6-E7-E8 VoDou Physics
model.
According to John
C. Baez and S. Jay Olson in their paper at gr-qc/0201030:
"... Ng and van Dam have argued that quantum theory and
general relativity give a lower bound delta L > L^(1/3)
L_P ^(2/3) on the uncertainty of any distance, where L is the
distance to be measured and L_P is the Planck length. Their idea
is roughly that to minimize the position uncertainty of a freely
falling measuring device one must increase its mass, but if its
mass becomes too large it will collapse to form a black hole. ...
Amelino-Camelia has gone even further, arguing that delta L
> L^(1/2) L_P ^(1/2) ... Here we show that one can go
below the Ng-van Dam bound [ and the Amelino-Camelia bound
] by attaching the measuring device to a massive elastic rod.
...
[ while the Ng-van Dam ] result was obtained by
multiplying two independent lower bounds on delta L, one from
quantum mechanics and the other from general relativity, ours
arises from an interplay between competing effects. On the one
hand, we wish to make the rod as heavy as possible to minimize the
quantum-mechanical spreading of its center of mass. To prevent it
from becoming a black hole, we must also make it very long. On the
other hand, as it becomes longer, the zero-point fluctuations of
its ends increase, due to the relativistic limitations on its
rigidity. We achieve the best result by making the rod just a bit
longer than its own Schwarzschild radius.
... Relativistic limitations on the rod's rigidity, together
with the constraint that its length exceeds its Schwarzschild
radius, imply that zero-point fluctuations of the rod give an
uncertainty delta L > L_P . ...".
( Here is some
History )
Here is an Introduction to VoDou
Physics.
The Truth Quark, through its strong
interaction with Higgs Vacua, may have two excited energy levels at
225 GeV and 173 GeV, above a ground state at 130 GeV. The 173
GeV excited state may exist due to appearance of a Planck-energy
vaccum with < phi_vac2 > = 10^19 GeV in addition to the
low-energy Standard Model vacuum with < phi_vac1 > = 252
GeV.
This Link goes to a Summary
of Results of D4-D5-E6-E7-E8 model calculations of Particle Masses
and Force Strength Constants, some of which are shown in this
chart:
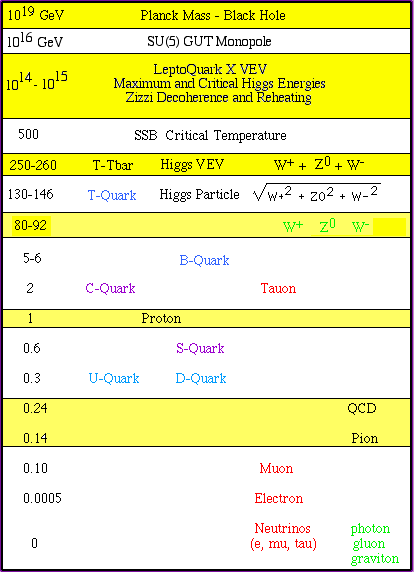
Here is how the mass ratios work:
It is interesting that
the ratio of the sum of the masses of the weak bosons W+, W-,
and W0 to the sum of the masses of the first generation fermions is
259.031 GeV / 7.508 GeV = 34.5007
which is very close to
the ratio of the geometric part of the Weak Force Strength to the
Electromagnetic Fine Structure Constant is 0.253477 / ( 1 / 137.03608
) = 34.7355.
Here are links to more details:
Details of that discrete
HyperDiamond Feynman Checkerboard model,
including calculation of particle masses
and charges, or force strength constants,
are in my 1997 paper
From Sets to Quarks:
Deriving the Standard Model plus Gravitation
from Simple Operations on Finite Sets.
Table of Contents:
Chapter 1 - Introduction.
Chapter 2 - From Sets to Clifford Algebras.
MANY-WORLDS QUANTUM THEORY.
Chapter 3 - Octonions and E8 lattices.
Chapter 4 - E8 spacetime and particles.
Chapter 5 - HyperDiamond Lattices.
Chapter 6 - Spacetime and Internal Symmetry Space.
Chapter 7 - Feynman Checkerboards.
Chapter 8 - Charge = Amplitude to Emit Gauge Boson.
Chapter 9 - Mass = Amplitude to Change Direction.
Chapter 10 - Protons, Pions, and Physical Gravitons.
Appendix A - Errata for Earlier Papers.
References.
Details of the D4-D5-E6 physics model,
which is substantially a continuum spacetime/LaGrangian version
of the HyperDiamond Feynman Checkerboard model,
are given in hep-ph/9501252
Gravity and the Standard Model from D4-D5-E6 Model
using 3x3 Octonion Matrices.
Another way to look at the continuum version of the D4-D4-E6 model
is in terms of Octonion Creators and Annihilators.
This is a more detailed rough outline,
but without full technical details, of
the model and how I visualize
it.
Here, I have not included technical references or
references to credit who did what and when.
They can be found in the other pages and papers
dealing with the D4-D5-E6-E7-E8 model.
In the early 1970s, just before the Standard Model
was established, Armand Wyler noticed something:
the electromagnetic fine structure constant
seemed to be related to the ratios of volumes
of bounded complex homogeneous domains
and their Shilov boundaries.
He did not give clear physical reasons for the
relationship, and his results were dismissed
by most physicists as mere coincidence.
However,
a few have followed his work with interest,
such as Gustavo R. Gonzlez-Martin, who has written
papers about the electromagnetic Fine Structure Constant
and other things from a point of view similar to that of Wyler.
The Discrete HyperDiamond Generalized
Feynman Checkerboard and Continuous
Manifolds are related by Quantum
Superposition:
Start with the Standard Model.
The Standard Model has 3 basic parts:
1. a spacetime
(You can think of spacetime as being
fundamentally a HyperDiamond Lattice, with the
continuous manifold being just a convenient
way to think of it for doing calculations
involving calculus, Lie groups, and such things.
As a Planck Scale Lattice, it violates Lorentz
Invariance at the Planck Scale.);
2. fermion particles and antiparticles,
such as electrons and quarks, that
roughly speaking are the matter in the model
(You can think of them as being things located
at points in the spacetime,
or vertices of the spacetime lattice); and
3. gauge bosons,
or particles that carry the forces between particles
(You can think of them as being "located" on
lines in spacetime connecting the particles
that are acting on each other,
or as being on links of the spacetime lattice).
The gauge group of a given force is the symmetry group
of the gauge bosons that carry the given force.
The Standard Model is made by taking the total gauge group
to be the Cartesian product of the 3 gauge groups
of the 3 forces
(electromagnetic, weak, and color).
In the Standard Model,
there is NO FUNDAMENTAL RELATION among the three parts.
The spacetime, fermion particles and antiparticles,
and gauge bosons are just put in by hand, so to speak.
Paul Langacker, in hep-ph/0304186,
says: "... The structure of the standard model is concisely
summarized, including the standard model Lagrangian, spontaneous
symmetry breaking, the reexpression of the Lagrangian in terms of
mass eigenstates after symmetry breaking, and the gauge interactions.
The problems of the standard model are described. ...".
Since Gravity can be formulated in terms of curvature of spacetime,
the force of Gravity
DOES have a FUNDAMENTAL RELATION to spacetime.
Try to Unify the Standard Model with Gravity.
Physicists tried to combine Gravity
with the Standard Model by treating Gravity
like the other forces, that is,
as a force described by a gauge group.
Their choice of gauge group for Gravity was
the 10-dimensional Poincare group of
spacetime translations (4-dim),
spacetime rotations (3-dim), and
spacetime Lorentz boosts (3-dim).
HOWEVER, the models whose unified simple Lie gauge group
contained the Cartesian product of the Poincare group
and the groups of the Standard Model
did not work well mathematically,
and soon
there was a theorem (Coleman-Mandula) saying that
there is NO WAY you can make a Cartesian product of
the Poincare group and the Standard Model groups
into a single simple unified Lie gauge group of
a mathematically consistent gauge field theory
over a 4-dimensional spacetime.
Supergravity.
Physicists did not just give up, they tried another way:
SUPERGRAVITY.
It avoided the Coleman-Mandula problem
by using Lie Superalgebras of Lie Supergroups
instead of Lie algebras of Lie groups.
Lie superalgebras are not simple Lie algebras,
but are combinations of two Lie algebras,
one of which is "bosonic" and the other "fermionic",
and defining their interactions with each other by using a
SUPERSYMMETRY between fermions and bosons.
The bosonic sector of the Lie Superalgebra should contain
both
the Lie algebra of the total Standard Model Lie group
and
a Lie algebra for gravity.
After playing around some, physicists realized that
the best Lie algebra for Supergravity theories
was not the 10-dim Poincare group,
but was the 10-dim deSitter group Spin(5),
or its noncompact version Spin(2,3).
Spin(5) is the covering group of 5-dim rotations,
and is
equal to 10-dim group Sp(2) related
to 2x2 matrices of quaternions.
Supergravity was very good because now gravity
was included, and there was a direct relation
between at leat one force and spacetime.
BUT AGAIN, A MATHEMATICAL PROBLEM CAME UP:
You could classify all the Lie Superalgebras,
and see which ones
had Spin(5)=Sp(2) for gravity.
The ones that worked had SO(N) as the other bosonic part.
SO(N) is the group of N-dim rotations.
Therefore, you could write down the equations
for the theory with one bosonic part SO(N)
and another bosonic part Spin(5)=Sp(2).
Such Lie Superalgebras were called
OrthoSymplectic osp(N,2).
You would get gravity just fine from
the bosonic part Spin(5)=Sp(2),
BUT you had to decide which N to use for SO(N)
and how to get the Standard Model groups
from the other bosonic part SO(N).
The mathematics of the model clearly showed
that the mathematically nicest N was N=8,
so that the other bosonic part should be SO(8),
BECAUSE OF THE OCTONIONIC STRUCTURE OF SO(8).
This N=8 Supergravity was also called
11-dimensional Supergravity, because
it could be formulated in 11-dimensional spacetime.
Since 11 = 4+7,
our physical 4-dimensional spacetime
could be seen as the result of compactifying,
or curling up into very small things,
the other 7-dimensions of 11-dim spacetime.
Since the compactified 7-dim things could
be thought of as 7-dimensional spheres,
and
since 7-dim spheres have a Malcev algebra
structure that is related to the Lie algebra of SO(8)
and
since the 7-dim sphere lives in 8-dim Octonion space
and is parallelizable by the 7-dim imaginary Octonions,
the underlying beauty of Supergravity is
DUE TO OCTONIONIC STRUCTURE.
HOWEVER,
the Supergravity model was constructed
using Lie Superalgebras
in such a way
that
SO(8) (interpreted that way) WAS NOT BIG ENOUGH TO
INCLUDE THE STANDARD MODEL GROUPS SU(3)xSU(2)xU(1).
There was also another problem with Supergravity:
The Supersymmetry of Supergravity was a naive
1-1 correspondence between fermions and bosons,
which said
"For every fermion there is a corresponding boson,
and vice versa."
SUCH NAIVE SUPERSYMMETRY HAS NEVER BEEN OBSERVED:
The fermions - neutrinos, electrons, quarks
ARE NOT
in 1-1 correspondence with
the gauge bosons - photon, weak bosons, gluons, gravitons.
Burton Richter, of SLAC,
says (in hep-ex/0001012):
"... The sociologists of science would say that our theories
are "socially constructed." That is certainly true initially
but our theoretical models are continually tested and the "social
constructs" that don't pass are discarded; though sometimes it
takes a long time. ... While the standard model has withstood all
experimental tests, we know that it is only a low-energy (a few
hundred GeV) approximation to a better model. The most popular
candidate to be the successor to the plain vanilla standard model
is supersymmetry. ... To the experimenters I would say that
supersymmetry is a pure "social construct" with no supporting
evidence despite many years of effort. It is okay to continue
looking for supersymmetry as long as it doesn't seriously
interfere with real work (top, Higgs, neutrinos, etc.). ...".
The D4-D5-E6-E7-E8 VoDou Physics model has a subtle
triality supersymmetry that is consistent with experiment
and useful in theory.
Although Supergravity had fatal flaws,
it had a nice underlying OCTONIONIC unity,
so the question was
How to use it as a basis for a better model?
Most physicists decided to:
1. Keep NAIVE 1-1 fermion-boson supersymmetry;
2. Give up SO(8) as a gauge group;
3. Generalize point-particle Spin(5)=Sp(2) gravity
to gravity based on String theory, the theory of
vibrating strings in N-dim spacetime.
Why vibrating strings?
In the conventional quantum mechanics courses
of the early education of most physicists,
they are drilled to think of the example of
the 1-dim harmonic oscillator - the vibrating string -
as the fundamental model in terms of which
physics theories should be visualized.
The result was Superstring theory.
Perturbative superstring theory can be formulated
in terms of 1-dimensional strings,
but
dualities in superstring theory can map perturbative string states
into non-perturbative states. Non-perturbative states can
correspond to p-dimensional membranes, called p-branes,
rather than 1-dimensional strings, so:
Duality forces superstring theory to include p-branes.
Since the resulting theory contains membranes
it is now usually termed M-theory.
The most elegant M-theory is 11-dimensional M-theory,
which is closely related to 11-dimensional supergravity.
As Bergman has pointed out,
"... the behavior of string theory at high temperature
and high longitudinal boosts, combined with ... p-branes ... ,
point to ... reformulation of strings, as well as p-branes,
as composits of bits. ..."
If the bits are thought of as pointlike 0-branes, then,
in view of the "... precise equivalence between
uncompactified eleven dimensional M-theory and
the N = infinity limit of the supersymmetric
matrix quantum mechanics describing D0-branes ..."
conjectured by Banks, Fischer, Shenker, and Susskind,
11-dimensional M-theory can be taken to mean M(atrix)-theory
as well as M(embrane)-theory.
Following Bergman, we see that at high energies
strings and p-branes break down into points,
so what we have is fundamentally a theory of pointlike bits,
of which strings and p-branes are only one low-temperature limit.
As Bergman says, the ".. main drawback of the string-bit models
is that there are so many of them. ... it is not clear yet
whether there is a unique superstring-bit model."
To construct a unique low-temperature model from
the high-temperature bit theory,
I propose to
start with a bunch of bits
and then
use the octonionic symmetries of 11-dimensional M-theory
as the basis for a theory of interaction among bits,
with the bits acting somewhat like the nodes of a spin network.
The result:
the D4-D5-E6-E7-E8 physics model emerges from the bits
just as it does from the points of
Simplex Physics above the Planck Energy
which is similar to its emergence
from the arrows of quantum set theory
and from the structure of Metaclifford algebras.
In my opinion:
supergravity in 11 dimensions;
superstring theory in 10 dimensions; and
M-theory in 11-dimensions
all have some nice features (mostly due to octonionic structures)
but all have the fatal flaw of NAIVE 1-1 fermion-boson supersymmetry
that has NEVER been observed experimentally,
while
the D4-D5-E6-E7-E8 physics model not only has nice octonion structure,
its subtle triality supersymmetry IS consistent with experiments.
However,
String Theory in 26 dimensions is useful,
not in its conventional interpretation,
but as a model of dynamics in the MacroSpace of Many-Worlds.
I did NOT go from Supergravity to Superstring theory.
I decided to go from Supergravity as follows:
1. Give up NAIVE 1-1 fermion-boson supersymmetry;
2. Keep SO(8) as a gauge group with Octonionic structure;
3. Give up Lie superalgebras and try to put
gravity into the SO(8).
To get everything from SO(8),
recall that the finite (Weyl group) reflection group
that generates SO(8) is the group of the
4-dimensional 24-cell.
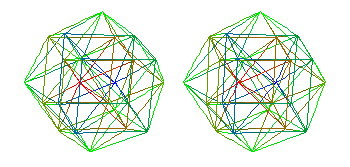
SO(8) has 28 generators:
24 for each vertex of the 24-cell
plus 4 for the dimensions of the 4-dim space of the 24-cell.
I let the 28 generators of SO(8) be the
generators of the gauge bosons:
8+3+1 = 12 of them for the Standard Model,
whose global group structure is discussed here;
the other 16 for a U(4),
which contains 15-dim SU(4)=Spin(6),
which contains 10-dim Spin(5)=Sp(2) for gravity.
The part of the U(4) not used for gravity
gives the Higgs mechanism and a complex phase for
quantum propagators.
If the 28-dim adjoint representation of SO(8)
gives the gauge bosons, then
WHAT GIVES SPACETIME?
SO(8) has an 8-dim vector representation,
as the 8-dim space on which the rotations act.
I let that space be an 8-dimensional spacetime.
Next,
WHAT GIVES FERMION PARTICLES AND ANTIPARTICLES?
Fermions should come from spinor representations,
but SO(8) has no spinor representations,
BUT its 2-fold covering group Spin(8)
DOES have TWO 8-dim half-spinor representations,
so I let one be 8 fermion particles
and the other be 8 fermion anti-particles.
In the D4-D5-E6-E7-E8 model, fermion masses can be calculated.
The tree-level constituent Truth Quark mass is 130 GeV.
The overall structure of the D4-D5-E6-E7-E8 model
involves Clifford Algebras and Conformal structures.
Subtle Triality
Supersymmetry:
Here is the Dynkin diagram for Spin(8).
Each vertex represents a representation of Spin(8),
with the center vertex (Spin(8)) corresponding
to the 28-dimensional adjoint representation
that I identified with gauge bosons.
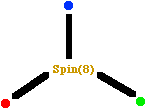
The three representations for
spacetime (blue dot),
fermion particles (red dot), and
fermion antiparticles (green dot)
are EACH 8-dimensional with Octonionic structure.
They are ALL isomorphic by the Spin(8) Triality Automorphism,
which can be represented by rotating or interchanging
the 3 arms of the Dynkin diagram of Spin(8).
The Triality isomorphism between spacetime
and fermion particles and fermion antiparticles
constitutes a
SUBTLE SUPERSYMMETRY between fermions and spacetime.
Ultraviolet finiteness of the D4-D5-E6-E7-E8 physics model
may be seen by considering, prior to dimensional reduction,
the generalized supersymmetry relationship between
the 28 gauge bosons
and
the 8 (first-generation) fermion particles and antiparticles.
In the 8-dimensional spacetime,
the dimension of each of the 28 gauge bosons in the Lagrangian is 1,
and
the dimension of each of the 8 fermion particles is 7/2,
so that
the total dimension 28x1 = 28 of the gauge bosons
is equal to
the total dimension 8x(7/2) = 28 of the fermion particles.
After dimensional reduction of spacetime to 4 dimensions,
the 8 fermions get a 3-generation structure
and
the 28 gauge bosons are decomposed to produce
the Standard Model of
U(1) electromagnetism, SU(2) weak force, and SU(3) color force,
plus a Spin(5) = Sp(2) gauge field
that can produce gravity by the MacDowell-Mansouri mechanism.
Note that both Gravity and the Standard Model forces are required
for the cancellations that produce the ultraviolet finiteness that is
useful in the Sakharov Zero Point
Fluctuation model of gravity.
The Conformal Structure of the
D4-D5-E6-E7-E8 model includes the symmetry of Conformal
Group Dilations, which transform the scale of
length/energy/mass, which gives the scale transformation properties
needed for Renormalization.
into 4-dim Internal Symmetry Space
and 4-dim Physical SpaceTime.
At this stage my D4-D5-E6-E7-E8 model has a problem:
Spacetime is 8-dim, not 4-dim.
HOWEVER, Ben Goertzel has noted that,
given a timestream of spacetime elements abababababababcca,
you need associativity for spacetime so that you can
mark off any given moment in a timestream
ababab|ababababcca
(by associating everything on either side of the moment)
without the choice of moment making a physical difference.
Since associativity of (ababab)(ababababcca) is required
so that a choice of moment does not change physics,
associativity is required for physical spacetime,
which must therefore be reduced from 8-dim octonion
to 4-dim associative quaternion.
Another way of seeing the Octonion Non-Associativity
point of view is to that the basis elements of
physical spatial dimensions should form Associative Triads
such as {i,j,k} among the Octonion Imaginaries {i,j,k,E,I,J,K}.
From yet another point of view,
dimensional reduction is needed for spacetime to have a
consistent lightcone structure.
Therefore physical timestreams and consistent lightcones
require that spacetime be an ASSOCIATIVE QUATERNIONIC SUBSPACE
of Octonionic 8-dim spacetime, and
the resulting math gives not only a 4-dim spacetime,
with -+++ signature (1,3),
but also
3 generations of fermions,
corresponding to the Lie algebras E6, E7, and E8,
and
the decomposition of the 28 gauge bosons into
the 12 gauge bosons of the Standard Model,
whose global group structure is discussed here,
plus
the 16-dim U(4) that gives Gravity, the Higgs mechanism,
and propagator phase.
The decomposition of the 28 gauge bosons can be seen from
different points of view:
Where does the associative quaternionic subspace come from?
Perhaps from timestream or conformal lightcones.
or perhaps equivalently from MetaClifford Algebra structure
or from Cohomology and Quadrics.
The Discrete HyperDiamond Generalized
Feynman Checkerboard and Continuous
Manifolds are related by Quantum
Superposition:
In the D4-D5-E6-E7-E8 VoDou Physics model, there are two
types of structures that might be regarded as
HyperSpace:
Merging Physical SpaceTime with
Internal Symmetry Space, to get a HyperSpace of Internal
Symmetry Space - this occurs at energies
above the quark/hadron phase transition;
and
Going from the Shilov
Boundary Physical SpaceTime into the Interior
of its Bounded Complex Domain, to get a HyperSpace
of Complex SpaceTime - this might occur at lower energies
for some phenomena, and only at very high energies for other
phenomena.
Real Complex
Physical SpaceTime 4-dim 8-dim
Internal Symmetry Space 4-dim 8-dim
Unified Physical+Internal 8-dim 16-dim
The relevant Complex Structure can be seen in such physical
concepts as Momentum Space,
Position-Momentum
Complementarity, Type IV(2)
Domains, Hyperspace,
Black Holes, Wavelets,
and Conformal
SpaceTime.
DIVISION ALGEBRAS - the largest division algebra,
the octonions, are reflexive/recursive
in that the 7 octonion imaginaries
correspond to the 7 associative triples;
MATRIX ALGEBRAS - symmetric JORDAN ALGEBRAS and
antisymmetric LIE ALGEBRAS -
the 248-dimensional E8 Lie Algebra
is the largest exceptional Lie algebra.
It is reflexive/recursive
in that its fundamental representation
is its adjoint representation;
LATTICES - the E8 lattice corresponds to "integral" octonions,
and has the same (finite) Coxeter/Dynkin diagram
as the E8 Lie algebra,
and
the 27-dim MacroSpace has a 26-dim subspace that
corresponds to the Lorentz Leech lattice /\25,1
of the Jordan algebra J3(O)o.
/\25,1 is reflexive/recursive
in that its Coxeter/Dynkin diagram
is the (infinite) Leech lattice /\24.
/\24 gives the Golay Code, and
the 196,560 units of /\24,
plus 300 = symmetric part of 24x24, plus 24,
give 196,884
which is the dimension of a representation space
of the largest sporadic finite simple group,
the Monster;
and
CLIFFORD ALGEBRAS - from which the other structures can be derived,
and which have the periodicity property
Cl(N+8) = Cl(N) x CL(8).
The Discrete HyperDiamond Generalized
Feynman Checkerboard and Continuous
Manifolds are related by Quantum
Superposition:
Symmetric Space Dimension Physical Interpretation
A0=D1 1 Real U(1) Electromagnetism
A1=B1=C1 3 Real SU(2) Weak Force
A2 8 Real SU(3) Color Force
A3=D3 15 Real Gravity+Higgs
D4 28 Real Gravity+Higgs+phase/U(1)xSU(2)xSU(3)
D5 / D4xU(1) 8 Complex SpaceTime
E6 / D5xU(1) 16 Complex Fermions
E7 / E6xU(1) 27 Complex MacroSpace of ManyWorlds
E8 / E7xSU(2) 28 Quaternionic ? Correlated Macrospace ?
These structures are motivated by Saul-Paul
Sirag's ideas about Weyl groups, A-D-E, and E7, and lead to
Jack Sarfatti's Back-Reaction structures
in MacroSpace.
Prior to dimensional reduction of spacetime from 8-dimensional to
4-dimensional,
the Lagrangian
for the D4-D5-E6-E7-E8 VoDou Physics model is
the Integral over the Cl(1,7) vector 1+7=8-dimensional SpaceTime
of
dd P' /\ * dd P + F /\ *F + S' D S + GF + GG
where
- d is the 8-dim covariant derivative
- P is the scalar field
- F is the adjoint Spin(8) curvature
- S' and S are half-spinor fermion spaces
- D is the 8-dim Dirac
operator
- GF is the gauge-fixing term
- GG is the ghost
term,
plus a topological Pontrjagin term.
The Pontrjagin term represents Instantons in 8-dimensional
spacetime that is locally RP1 x S7. Since, after dimensional
reduction of spacetime from 8 to 4 dimensions, the Pontrjagin term
goes into the Spin(6) conformal gravity sector of the D4-D5-E6-E7-E8
VoDou physics model, it does not go to the SU(3) color force sector.
Therefore, the SU(3) color force Sector has no THETA-term and the
D4-D5-E6-E7-E8 Vodou Physics model has no theoretical THETA-CP
problem.
After dimensional reduction to 4-dimensional
spacetime, the S7 of RP1 x S7 is factored by the Hopf fibration S3
-> S7 -> S4 into 4-dimensional spacetime that is locally RP1 x
S3, plus a CP2 part related to 4-dimensional Internal Symmetry
Space.
Reduction also produces, for each World of the Many-Worlds,
a 4-dimensional lattice Spacetime with MacDowell-Mansouri Gravity, a
Higgs Mechanism, and a Complex Propagator Phase;
a 4-dimensional lattice Internal Symmetry Space with 8 Color Force
Gluons, 3 Weak Force Bosons, and a Photon that live on the links of
the lattice Spacetime; and 3 generations of 8 Fermion Particles and 8
Fermion AntiParticles that live on the vertices of the lattice
Spacetime.
In terms of a 5-level grading of the E6 Lie algebra, that is, the
Graded Lie Alagebra of type e7,
we have
E6(-14) =
8-dim
+ 16-dim
+ R + so(1,7) + iR
+ 16-dim
+ 8-dim
with physical interpretation in the Lagrangian
of the D4-D5-E6-E7-E8 VoDou Physics Model
as:
- 8-dim of g(-2) plus R of g(0) plus 8-dim of
g(2), an 8-Complex-dimensional domain plus an R generator of
Complex U(1) symmetry, with an 8-real-dimensional Shilov
boundary of the form S1 x S7, corresponds to an 8-dimensional
spacetime base manifold over which the Lagrangian integral is
integrated;
- so(1,7) of g(0), the double
cover of the Lorentz group over the Octonions, corresponds to
the 28 generators of gauge bosons in the curvature term of the
Lagrangian integrand; and
- 16-dim of g(-1) plus iR of g(0) plus 16-dim of
g(1), a 16-Complex-dimensional domain, the Complexified
Octonion Plane (CxO)P2, plus an iR generator of Complex
U(1) symmetry, with a Shilov boundary ( not
entirely real, as the 16-Complex-dimensional domain is not of tube
type ) that may be regarded as being a bundle made up of a
real fibre S1 x S7 over a base space made up of S1 and CP4
( note that the CP4 has embedded S7 structure
), so that the real fibre S1 x S7 represents 8
first-generation fermion particles in the Dirac spinor term of
the Lagrangian integrand, and an S1 x S7 in the base space
represents 8 corresponding antiparticles.
Related Graded Lie Algebra structures
give:
Tony Smith's Home Page
......
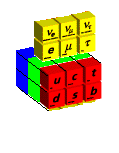
 D4 D5 E6 E7
Spin(8) Spin(10)
28 8 (+1+8) 16 (+1+16) 27 (+1+27)
Generation-1
Gravity SpaceTime Fermions
16-U(4) 4 8 MacroSpace
Generation-1 of
Standard Model Internal Space AntiFermions Many-Worlds
12-SU(3)xSU(2)xU(1) 4 8
D4 D5 E6 E7
Spin(8) Spin(10)
28 8 (+1+8) 16 (+1+16) 27 (+1+27)
Generation-1
Gravity SpaceTime Fermions
16-U(4) 4 8 MacroSpace
Generation-1 of
Standard Model Internal Space AntiFermions Many-Worlds
12-SU(3)xSU(2)xU(1) 4 8 



