Tony Smith's Home Page
Deriving the Standard Model plus Gravitation
from Simple Operations on Finite Sets
by Tony Smith
Table of Contents:
Chapter 1 - Introduction.
Chapter 2 - From Sets to Clifford Algebras.
Chapter 3 - Octonions and E8 lattices.
Chapter 4 - E8 spacetime and particles.
Chapter 5 - HyperDiamond Lattices.
Chapter 6 - Spacetime and Internal Symmetry Space.
Chapter 7 - Feynman Checkerboards.
Chapter 8 - Charge = Amplitude to Emit Gauge Boson.
Chapter 9 - Mass = Amplitude to Change Direction.
Higgs Scalar, Gauge Bosons, and Fermions.
Higgs Scalar Mass.
Gauge Boson Masses.
Weak Boson Masses.
Parity Violation,
Effective Masses,
and Weinberg Angle.
Fermion Masses.
Renormalization.
Perturbative QCD.
Chiral Perturbation Theory.
Lattice Gauge Theory.
Truth Quark Mass.
Other Fermion Masses.
First Generation.
Tauon Mass.
Beauty Quark Mass.
Muon Mass.
Strange Quark Mass.
Charm Quark Mass.
K-M Parameters.
Khokhlov: Nth Generation Fermions
and N-Photon Processes (N=1,2,3).
Chapter 10 - Protons, Pions, and Physical Gravitons.
Appendix A - Errata for Earlier Papers.
References.
Mass = Amplitude to Change Direction.
In the HyperDiamond Feynman Checkerboard model
the mass parameter m is the amplitude for a particle
to change its spacetime direction. Massless particles
do not change direction, but continue on the same
lightcone path.
In the D4-D6-E6-E7 Lagrangian continuum version
of this physics model, particle masses are calculated in terms
of relative volumes of bounded complex homogeneous domains and
their Shilov boundaries.
The relationship between
the D4-D6-E6-E7 Lagrangian continuum approach
and
the HyperDiamond Feynman Checkerboard discrete approach
is that:
the bounded complex homogeneous domains correspond to
harmonic functions of generalized Laplacians
that determine heat equations, or diffusion equations;
while the amplitude to change directions in the
HyperDiamond Feynman Checkerboard is a diffusion process
in the HyperDiamond spacetime, also corresponding to
a generalized Laplacian.
Details of the D4-D6-E6-E7 Lagrangian continuum approach
can be found on the World Wide Web at URLs
http://xxx.lanl.gov/abs/hep-ph/9501252
For the discrete HyperDiamond Feynman Checkerboard
approach of this paper, the only free mass parameter
is the mass of the Higgs scalar. All other particle
masses are determined as ratios with respect to the
Higgs scalar and each other.
The Higgs mass is 145.789 GeV in the
HyperDiamond Feynman Checkerboard model,
since the Higgs Scalar field vacuum expectation value v
is set at 252.514 GeV, a figure chosen so
that the mass ratios of the model will give an electron
mass of 0.5110 MeV.
Here is how the mass ratios work:
It is interesting that
the ratio of the sum of the masses of the weak bosons W+, W-,
and W0 to the sum of the masses of the first generation fermions is
259.031 GeV / 7.508 GeV = 34.5007
which is very close to
the ratio of the geometric part of the Weak Force Strength to the
Electromagnetic Fine Structure Constant is 0.253477 / ( 1 / 137.03608
) = 34.7355.
Effectively, in the HyperDiamond Feynman
Checkerboard model, the electron mass is fixed at 0.5110 MeV
and all other masses are determined from it by the
ratios calculated in the model.
Higgs
Scalar, Gauge Bosons, and Fermions.
Recall from Chapter 4 that 16x16 = 256-dimensional DCl(0,8)
has graded structure
1 8 28 56 70 56 28 8 1
that gives three types of particles for which mass ratios
can be calculated in the HyperDiamond Feynman Checkerboard
model:
the Higgs Scalar;
the 28 bivector gauge bosons;
and the 8 + 8 = 16 half-spinor fermions.
There is only one Higgs scalar. Its mass is 145.789 GeV.
Gauge Boson Masses.
After dimensional reduction to 4-dimensional spacetime,
the 28 Spin(0,8) gauge bosons split into two groups:
12 Standard Model gauge bosons, which are
8 SU(3) gluons,
3 SU(2) weak bosons, and
1 U(1) photon,
which 12 gauge bosons see Internal Symmetry Space
according to their group symmetry;
and
16 U(4) gauge bosons,
which reduce to 15 SU(4) = Spin(6) gauge bosons
plus one U(1) phase for particle propagator amplitudes
(this phase is what makes the sum-over-histories quantum
theory interferences work).
The 15 SU(4) = Spin(6) gauge bosons further reduce
to 10 Spin(5) deSitter gravitons that give physical
gravity by the MacDowell-Mansouri mechanism as described in
http://xxx.lanl.gov/abs/hep-ph/9501252
with gravitons that see their Symmetry Space
of Spacetime according to their group symmetry,
and 4 conformal generators and 1 scale generator.
The 4 conformal generators couple to the Higgs scalar
so that it becomes the mass-giver by the Higgs mechanism
as described in
http://xxx.lanl.gov/abs/hep-ph/9501252
and the 1 scale generator
represents the scale that we chose
by setting the Higgs scalar field vacuum expectation
value v to be 252.514 GeV.
All these gauge bosons are massless at very high energies,
but at energies comparable to the Higgs mass and below,
the Higgs scalar couples to the SU(2) weak bosons
to give them mass.
Denote the 3 SU(2) high-energy weak bosons
(massless at energies higher than the electroweak unification)
by W+, W-, and W0, corresponding to the massive
physical weak bosons W+, W-, and Z0.
The triplet { W+, W-, W0 }
couples directly with the T - Tbar quark-antiquark pair,
so that the total mass of the triplet { W+, W-, W0 }
at the electroweak unification
is equal to the total mass of a T - Tbar pair, 259.031 GeV.
The triplet { W+, W-, Z0 }
couples directly with the Higgs scalar,
which carries the Higgs mechanism by
which the W0 becomes the physical Z0,
so that the total mass of the triplet { W+, W-, Z0 }
is equal to the vacuum expectation value v of
the Higgs scalar field, v = 252.514 GeV.
What are individual masses of members
of the triplet { W+, W-, Z0 } ?
First, look at the triplet { W+, W-, W0 }
which can be represented by the 3-sphere S^3.
The Hopf fibration of S^3 as
S^1 --} S^3 --} S^2
gives a decomposition of the W bosons
into the neutral W0 corresponding to S^1 and
the charged pair W+ and W- corresponding
to S^2.
The mass ratio of the sum of the masses of
W+ and W- to
the mass of W0
should be the volume ratio of
the S^2 in S^3 to
the S^1 in S3.
The unit sphere S^3 in R^4 is
normalized by 1 / 2.
The unit sphere S^2 in R^3 is
normalized by 1 / sqrt3.
The unit sphere S^1 in R^2 is
normalized by 1 / sqrt2.
The ratio of the sum of the W+ and W- masses to
the W0 mass should then be
(2 / sqrt3) V(S^2) / (2 / sqrt2) V(S^1) = 1.632993.
Since the total mass of the triplet { W+, W-, W0 }
is 259.031 GeV, the total mass of a T - Tbar pair,
and the charged weak bosons have equal mass,
we have
mW+ = mW- = 80.326 GeV,
and mW0 = 98.379 GeV.
Parity Violation, Effective Masses,
and Weinberg Angle.
The charged W+/- neutrino-electron interchange
must be symmetric with the electron-neutrino interchange,
so that the absence of right-handed neutrino particles requires
that the charged W+/- SU(2)
weak bosons act only on left-handed electrons.
Each gauge boson must act consistently
on the entire Dirac fermion particle sector,
so that the charged W+/- SU(2) weak bosons
act only on left-handed fermions of all types.
The neutral W0 weak boson does not interchange Weyl
neutrinos with Dirac fermions, and so is not restricted
to left-handed fermions,
but also has a component that acts on both types of fermions,
both left-handed and right-handed, conserving parity.
However, the neutral W0 weak bosons are related to
the charged W+/- weak bosons by custodial SU(2)
symmetry, so that the left-handed component of the
neutral W0 must be equal to the left-handed (entire)
component of the charged W+/-.
Since the mass of the W0 is greater than the mass
of the W+/-, there remains for the W0 a component
acting on both types of fermions.
Therefore the full W0 neutral weak boson interaction
is proportional to
(mW+/-^2 / mW0^2) acting on left-handed fermions
and
(1 - (mW+/-^2 / mW0^2)) acting
on both types of fermions.
If (1 - (mW+/-2 / mW0^2)) is defined to be
sin(thetaw)^2 and denoted by K, and
if the strength of the W+/- charged weak force
(and of the custodial SU(2) symmetry) is denoted by T,
then the W0 neutral weak interaction can be written as:
W0L = T + K and W0LR = K.
Since the W0 acts as W0L with respect to the
parity violating SU(2) weak force and
as W0LR with respect to the parity conserving U(1)
electromagnetic force of the U(1) subgroup of SU(2),
the W0 mass mW0 has two components:
the parity violating SU(2) part mW0L that is
equal to mW+/- ; and
the parity conserving part mW0LR that acts like a
heavy photon.
As mW0 = 98.379 GeV = mW0L + mW0LR, and
as mW0L = mW+/- = 80.326 GeV,
we have mW0LR = 18.053 GeV.
Denote by *alphaE = *e^2 the force
strength of the weak parity conserving U(1)
electromagnetic type force that acts through the
U(1) subgroup of SU(2).
The electromagnetic force strength
alphaE = e^2 = 1 / 137.03608 was calculated
in Chapter 8 using
the volume V(S^1) of an S^1 in R^2,
normalized by 1 / \qrt2.
The *alphaE force is part of the SU(2) weak
force whose strength alphaW = w^2 was calculated
in Chapter 8 using the volume V(S^2) of an S^2 \subset R^3,
normalized by 1 / sqrt3.
Also, the electromagnetic force strength alphaE = e^2
was calculated in Chapter 8 using a
4-dimensional spacetime with global structure of
the 4-torus T^4 made up of four S^1 1-spheres,
while the SU(2) weak force strength
alphaW = w^2 was calculated in Chapter 8
using two 2-spheres S^2 x S^2,
each of which contains one 1-sphere of
the *alphaE force.
Therefore
*alphaE = alphaE ( sqrt2 / sqrt3)(2 / 4) = alphaE / sqrt6,
*e = e / (4th root of 6) = e / 1.565 , and
the mass mW0LR must be reduced to an effective value
mW0LReff = mW0LR / 1.565 = 18.053/1.565 = 11.536 GeV
for the *alphaE force to act like
an electromagnetic force in the 4-dimensional
spacetime HyperDiamond Feynman Checkerboard model:
*e mW0LR = e (1/5.65) mW0LR = e mZ0,
where the physical effective neutral weak boson is
denoted by Z0.
Therefore, the correct HyperDiamond Feynman Checkerboard values for
weak boson masses and the Weinberg angle thetaW are:
mW+ = mW- = 80.326 GeV;
mZ0 = 80.326 + 11.536 = 91.862 GeV; and
sin(thetaW)^2 = 1 - (mW+/- / mZ0)^2 =
= 1 - ( 6452.2663 / 8438.6270 ) = 0.235.
Radiative corrections are not taken into account here,
and may change these tree-level
HyperDiamond Feynman Checkerboard values somewhat.
According to hep-ex/0205080:
"... The NuTeV experiment has performed precision
measurements of the ratio of neutral-current to charged-current
cross-sections in high rate, high energy neutrino and
anti-neutrino beams on a dense, primarily steel, target. The
separate neutrino and anti-neutrino beams, high statistics, and
improved control of other experimental systematics, allow the
determination of electroweak parameters with significantly greater
precision than past nu-N scattering experiments. Our null
hypothesis test of the standard model prediction measures ...
sin(theta_W^(on-shell))^2 = 0.22773 +/- 0.00135 (stat) +/-
0.00093 (syst)
- 0.00022 x ( ( M_top^2 - ( 175 GeV/c^2 )^2 ) / ( 50 GeV/c^2
)^2 )
+ 0.00032 ln( M_Higgs / 150 GeV )
... A fit to the precision electroweak data, excluding neutrino
measurements, predicts a value of 0.2227 +/- 0.00037 ...
approximately 3 sigma from the NuTeV measurement. In the on-shell
scheme ... sin(theta_W)^2 = 1 - ( M_W / M_Z )^2 , where M_W and
M_Z are the physical gauge boson masses; therefore, this result
implies M_W = 80.14 +/- 0.08 GeV ... The world-average of the
direct measurements of M_W is 80.45 +/- 0.04 GeV ... A fit to
precision data ... including NuTeV, has been performed by the
LEPEWWG ... shown in Figure 1 ...
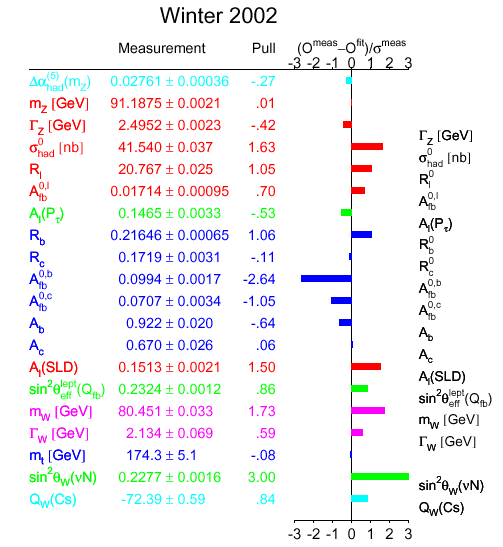
... This suggests that in the context of all the precision
data, as compiled by the LEPEWWG, the NuTeV result is still a
statistical anomaly suffcient to spoil the fit if the standard
model is assumed. ....".
Note that there are several currently accepted ways to define the
Weinberg angle. According to a
19 November 2001 document of the
Particle Data Group, "...
 ...
...
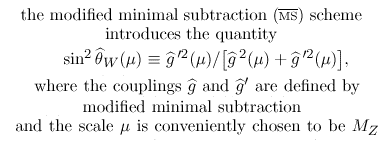 ...".
...".
The D4-D5-E6-E7-E8 VoDou Physics
model definition of the Weinberg angle is fundamentally based on
force strengths (which, in turn, can be expressed in terms of the
calculated W and Z weak boson masses of M_W =
80.326 GeV and M_Z = 91.862 GeV), so that
the D4-D5-E6-E7-E8 VoDou Physics
model definition of the Weinberg angle is effectively the
MSbar definition.
In the edited-quotes of the above images, c and cbar are functions
of the masses of the Higgs and the Truth Quark, and the above numbers
may be based on masses of around 100 GeV and 175 GeV, respectively.
Even so, using those values of c and cbar, a calculation shows that
the MSbar value of sin(theta_W)^2 of 0.235 of the D4-D5-E6-E7-E8
VoDou Physics model corresponds to an on-shell tree level
value of sin(theta_W)^2 of 0.2267.
The hep-ex/0205080
on-shell value for the NuTeV experimental result for sin(theta_W)^2 =
0.2277 assumes that the Higgs Mass
M_Higgs = 150 GeV and that the Truth Quark
Mass M_top = 175 GeV.
In the D4-D5-E6-E7-E8 VoDou Physics
model, the Higgs Mass of 146 GeV is
close to 150 GeV, but the Truth Quark Mass of
130 GeV is substantially lower than 175 GeV. If the value of 130 GeV
is used for the Truth Quark Mass in the equation of hep-ex/0205080,
then the value of sin(theta_W)^2 is increased by
0.00022 x ( 175^2 - 130^2 ) / 50^2 = 0.0012 GeV
giving for the on-shell value for the NuTeV experimental result
with a 130 GeV Truth Quark Mass sin(theta_W^nu-N)^2 = 0.2289 with
total statistical and systematic error bar +/- 0.00228, which
compares (in my opinion) realistically with the D4-D5-E6-E7-E8
VoDou Physics model on-shell tree level value of sin(theta_W)^2
of 0.2267.
Therefore I do not agree with the conclusion of hep-ex/0205080
that "... the NuTeV result is still a statistical anomaly sufficient
to spoil the fit if the standard model is assumed ...".
Corresponding to the way that 24
of the 28 Gauge Bosons of the
D4-D5-E6-E7-E8 VoDou Physics model can be represented
by the vertices of a 24-cell, the
first-generation Fermion Particles and anti-Particles, and
SpaceTime plus Internal Symmetry
Space, can be represented by the vertices of a
dual 24-cell:
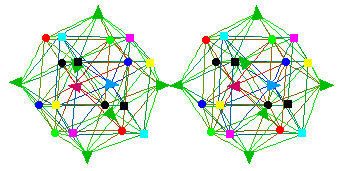
In the dual 24-cell, the 8 vertices

represent the first-generation electron; red, green, blue up
quarks; red, green, blue down quarks, and neutrino. The 8 vertices
representing the first-generation antiparticles are denoted by the
cyan, magenta, yellow, and square-black vertices.
These 8+8 = 16 vertices correspond to the 16 Complex Dimensions of
the Bounded Domain corresponding to the
Symmetric Space E6
/ D5xU(1), and to the 16 Real Dimensions of its Shilov
Boundary. The 32 Real Dimensions of that Complex Bounded Domain
correspond to the 32 vertices of the
5-dimensional HyperCube that make up 32 of the 72
E6 root vectors.
In this image
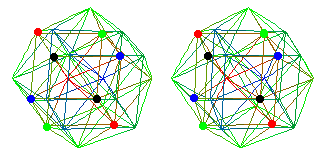
only the 8 vertices representing the first-generation fermion
particles are marked.
First generation fermion particles are also represented
by octonions as follows:
Octonion Fermion
Basis Element Particle
1 e-neutrino
i red up quark
j green up quark
k blue up quark
E electron
I red down quark
J green down quark
K blue down quark
First generation fermion antiparticles are represented
by octonions in a similiar way.
Second generation fermion particles and antiparticles
are represented by pairs of octonions.
Third generation fermion particles and antiparticles
are represented by triples of octonions.
In the HyperDiamond Feynman Checkerboard model,
there are no higher generations of fermions than the Third.
This can be seen algebraically as a consequence of the
fact that the Lie algebra series E6, E7, and E8,
has only 3 algebras, which in turn is a consequence of
non-associativity of octonions, as described here and in
http://www.innerx.net/personal/tsmith/E678.html
or geometrically as a consequence of the fact that,
if you reduce the original 8-dimensional spacetime
into associative 4-dimensional physical spacetime
and coassociative 4-dimensional Internal Symmetry Space,
then, if you look in the original 8-dimensional spacetime
at a fermion (First-generation represented by a single octonion)
propagating from one vertex to another,
there are only 4 possibilities for the same propagation
after dimensional reduction:
1 - the origin and target vertices are both
in the associative 4-dimensional physical spacetime,
in which case the propagation is unchanged, and the
fermion remains a FIRST generation fermion represented
by a single octonion;
2 - the origin vertex is in the associative spacetime,
and the target vertex in in the Internal Symmetry Space,
in which case there must be a new link from
the original target vertex in the Internal Symmetry Space
to a new target vertex in the associative spacetime,
and a second octonion can be introduced at the original
target vertex in connection with the new link,
so that the fermion can be regarded after dimensional reduction
as a pair of octonions, and therefore as a SECOND generation fermion;
3 - the target vertex is in the associative spacetime,
and the origin vertex in in the Internal Symmetry Space,
in which case there must be a new link to
the original origin vertex in the Internal Symmetry Space
from a new origin vertex in the associative spacetime,
so that a second octonion can be introduced at the original
origin vertex in connection with the new link,
so that the fermion can be regarded after dimensional reduction
as a pair of octonions, and therefore as a SECOND generation fermion;
and
4 - both the origin vertex and the target vertex
are in the Internal Symmetry Space,
in which case there must be a new link to
the original origin vertex in the Internal Symmetry Space
from a new origin vertex in the associative spacetime,
and a second new link from the original target vertex
in the Internal Symmetry Space to a new target vertex
in the associative spacetime,
so that a second octonion can be introduced at the original
origin vertex in connection with the first new link,
and a third octonion can be introduced at the original
target vertex in connection with the second new link,
so that the fermion can be regarded after dimensional reduction
as a triple of octonions, and therefore as a THIRD generation fermion.
As there are no more possibilities, there are no more generations.
RENORMALIZATION OF PARTICLE MASSES AND FORCE STRENGTHS:
Particle masses and force strength constants
are not really "constant" when you measure them,
as the result of your measurement will depend on
the energy at which you measure them.
Measurements at one energy level can be related to
measurements at another by renormalization equations.
The particle masses calculated in
the D4-D6-E6-E7-E7-E8 VoDou Physics model
are, with respect to renormalization, each defined at
the energy level of the calculated particle mass.
In the D4-D6-E6-E7-E7-E8 VoDou Physics model,
Dilatation Scale Transformations
of the Conformal Group provide a natural setting for
the Renormalization Group Process.
For leptons, such as the electron, muon, and tauon,
which carry no color charge,
you can renormalize conventionally from that energy level
to "translate" the result to another energy level,
because those particles are not "confined" and
so can be experimentally observed as "free particles"
("free" means "not strongly bound to other particles,
except for virtual particles of the active vacuum of spacetime").
For quarks, which are confined and
cannot be experimentally observed as free particles,
the situation is more complicated.
In the D4-D6-E6-E7-E8 VoDou Physics model,
the calculated quark masses are considered to be constituent masses.
In hep-ph/9802425,
Di Qing, Xiang-Song Chen, and Fan Wang,
of Nanjing University, present a qualitative QCD analysis
and a quantitative model calculation
to show that the constituent quark model
[after mixing a small amount (15%) of sea quark components]
remains a good approximation
even taking into account the nucleon spin structure
revealed in polarized deep inelastic scattering.
The effectiveness of
the NonRelativistic model of light-quark hadrons
is explained by, and affords experimental Support for,
the Quantum Theory of David Bohm.
Consitituent particles are Pre-Quantum particles
in the sense that their properties are calculated
without using sum-over-histories Many-Worlds quantum theory.
("Classical" is a commonly-used synonym for "Pre-Quantum".)
Since experiments are quantum sum-over-histories processes,
experimentally observed particles are Quantum particles.
The lightest experimentally observable particle
containing quarks is the pion,
which is a quark-antiquark pair made up of the lightest
quarks, the up and down quarks.
A quark-antiquark pair is the carrier of the strong force,
and mathematically resembles a bivector gluon,
which is the carrier of the color force.
The charactereistic energy level of pions is
the square root of the sum of the squares of
the masses of the two charged and one neutral pion.
It is about 245 MeV (to more accuracy 241.4 MeV).
The gluon-carried color force strength is renormalized
to higher energies from about 245 MeV in the conventional way.
What about quarks, as opposed to gluons?
Gluons are represented by quark-antiquark pairs,
but a quark is a single quark.
The lightest particle containing a quark that is not
coupled to an antiquark is the proton,
which is a stable (except with respect to quantum gravity)
3-quark color neutral particle.
The characteristic energy level of the proton
is about 1 GeV (to more accuracy 938.27 MeV).
Quark masses are renormalized to higher energies
from about 1 GeV (or from their calculated mass,
below which they do not exist except virtually)
in the conventional way.
What about the 3 quarks (up, down, and strange)
that have constituent masses less than 1 GeV?
Below 1 GeV, they can only exist
(if not bound to an antiquark) within a proton,
so their masses are "flat", or do not "run",
in the energy range below 1 GeV.
Since the 3 quarks, up, down, and strange,
are the only ones lighter than a proton,
they can be used as the basis for a useful
low-energy theory, Chiral Perturbation Theory,
that uses the group SU(3)xSU(3),
or, if based only on the lighter up and down quarks
that uses the group SU(2)xSU(2).
A useful theory at high energies,
much above 1 GeV, is Perturbative QCD,
that treats the quarks and gluons as free,
which they are asymptotically
as energies become very high.
However,
Patrascioiu and Seiler indicate
that Perturbative QCD may not be exactly physically accurate.
Further,
Alexei Morozov and Antti J. Niemi, in their
paper, Can Renormalization Group Flow End in a Big Mess?,
hep-th/0304178, say: "... The field theoretical renormalization
group equations have many common features with the equations of
dynamical systems. In particular, the manner how Callan-Symanzik
equation ensures the independence of a theory from its subtraction
point is reminiscent of self-similarity in autonomous flows towards
attractors. Motivated by such analogies we propose that besides
isolated fixed points, the couplings in a renormalizable field theory
may also flow towards more general, even fractal attractors. This
could lead to Big Mess scenarios in applications to
multiphase systems, from spin-glasses and neural networks to
fundamental ... theory. We argue that ... such chaotic flows ... pose
no obvious contradictions with the known properties of effective
actions, the existence of dissipative Lyapunov functions, and even
the strong version of the c-theorem. We also explain the difficulties
encountered when constructing effective actions with chaotic
renormalization group flows and observe that they have many common
virtues with realistic field theory effective actions. We conclude
that if chaotic renormalization group flows are to be excluded,
conceptually novel no-go theorems must be developed. ... in the
classical Yang-Mills theory chaotic behaviour has already been well
established ... Consequently such chaotic behaviour will not be
considered here. Obviously, a chaotic RG flow also necessitates the
consideration of field (string) theories with at least three
couplings. In the present article we shall be interested in the
possibility of chaotic RG flows in the IR limits of quantum field and
string theories. ... we consider limit cycles from the point of view
of RG flows, and inspect vorticity as a RG scheme independent tool
for describing multicoupling flows. ... we explain how to construct
model effective actions from the beta-function flows. In particular,
we explain how the construction fails in case of chaotic flows and
suggests this parallels the problems encountered in constructing
actual field theory effective actions. This also explains why it is
very hard to construct actual field theory models with chaotic RG
flow. ...".
Perturbative QCD, Chiral Perturbation Theory, and Lattice
Gauge Theory:
Even though, as Patrascioiu and Seiler indicate,
Perturbative QCD may not be exactly physically accurate,
Perturbative QCD can be useful in doing rough calculations
and in understanding some aspects of QCD.
To do calculations in theories such as
Perturbative QCD and Chiral Perturbation Theory,
you need to use effective quark masses that
are called current masses. Current quark masses are different
from the Pre-Quantum constituent quark masses of our model.
The current mass of a quark is defined in our model as
the difference between
the constituent mass of the quark
and
the density of the lowest-energy sea of virtual gluons,
quarks, and antiquarks, or 312.75 MeV.
Since the virtual sea is a quantum phenomenon,
the current quarks
of Perturbative QCD and Chiral Perturbation Theory are,
in my view, Quantum particles.
The relation between current masses and constituent masses
may be explained, at least in part,
by the Quantum Theory of David Bohm.
From a conventional point of view,
in hep-ph/0006306, Szczepaniak and Swanson
"... have shown how quark model phenomenology
may be derived from a simple model of QCD
through the careful use of a nonperturbative renormalization
procedure coupled with a model of the vacuum
which breaks chiral symmetry. ...".
In our model:
a current quark is viewed as a composite combination
of a fundamental constituent quark
and Quantum virtual sea gluon, quarks, and antiquarks
(compare the conventional picture of, for example,
hep-ph/9708262, in which current quarks are Pre-Quantum
and constituent quarks are Quantum composites); and
the input current quarks of
Perturbative QCD and Chiral Perturbation Theory
are Quantum, and not Pre-Quantum, so that we view
Perturbative QCD and Chiral Perturbation Theory as
effectively "second-order" Quantum theories
(rather than fundamental theories)
that are most useful in describing phenomena
at high and low energy levels, respectively.
Therefore,
in Perturbative QCD and Chiral Perturbation Theory,
the up and down quarks roughly massless.
One result is that the current masses
can then be used as input for
the SU(3)xSU(3) Chiral Perturbation Theory
that, although it is only approximate because the
constituent mass of the strange quark is about 312 MeV,
rather than nearly zero,
can be useful in calculating meson properties.
Taekoon Lee, in hep-ph/0006349, points out that quark mass
aligns the theta vacuum so that there is no strong CP violation,
thus solving the QCD strong CP problem without an axion.
This result can also be seen from
the point of view of the D4-D5-E6-E7 physics model.
WHAT ARE THE REGIONS OF VALIDITY OF PERTURBATIVE QCD
and CHIRAL PERTURBATION THEORY?
Perturbative QCD is useful at high energies.
If Perturbative QCD is valid at energies above 4.5 GeV,
then Yndurian in hep-ph/9708300 has shown that
lower bounds for current quark masses are:
ms at least 150 MeV (compare D4-D6-E6-E7 312 MeV)
mu+md at least 10 MeV (compare D4-D6-E6-E7 6.5 MeV)
mu-md at least 2 MeV (compare D4-D6-E6-E7 2.1 MeV)
Yndurian bases his estimates on positivity,
and uses MSbar masses defined at 1 Gev^2.
Chiral Perturbation Theory is useful at low energies.
Lellouch, Rafael, and Taron in hep-ph/9707523 have shown
roughly similar lower bounds using Chiral Perturbation Theory.
Lattice Gauge Theory calculations of Gough et al in hep-ph/9610223
give light quark current MSbar masses at 1 Gev^2 as:
ms 59 to 101 MeV
mu+md 4.6 to 7.8 MeV
Clearly,
the strange quark current masses of Lattice Gauge Theory
are a lot lighter than those calculated by
Perturbative QCD and Chiral Perturbation Theory,
as well as the D4-D6-E6-E7 model.
Further, recent observation of the decay of K+ to
pion+ and a muon-antimuon pair gives a branching ratio
with respect to the decay of K+ to pion+ and e+ e-
that is 0.167, which is about 2 sigma below the
Chiral Perturbation Theory prediction of 0.236.
These facts indicate that Perturbative QCD,
Chiral Perturbation Theory, and Lattice Gauge Theory
are approximations to fundamental theory,
each useful in some energy regions,
but not fully understood in all energy regions.
Conventional Lattice Gauge Theory for fermions, such as quarks,
has some fundamental problems:
The conventional lattice Dirac operator is afflicted with the
Fermion Doubling Problem, in which nearest-neighbor lattice sites are
occupied with (for 4-dim spacetime) 2^4 = 16 times too many
fermions;.
The conventional solutions to the Fermion Doubling Problem are to
add non-local terms that violate Chiral Symmetry on the lattice. If
you are trying to do Chiral Perturbation Theory on the lattice, that
seems to be a bad idea.
To solve the Fermion Doubling Problem without violating Chiral
Symmetry, Bo Feng,
Jianming Li, and Xingchang Song have proposed to modify the
conventional lattice Dirac operator by adding a non-local term that
(like an earlier approach of Drell et. al., Phys. Rev. D 14 (1976)
1627) couples all lattice sites along a given direction instead of
coupling only nearest-neighbor sites. Their modified lattice Dirac
operator not only preserved Chiral Symmetry, it also gives the
conventional D'Alembertian operator, and they are able to construct
the Weinberg-Salam Electro-Weak model on a lattice.
Conventional Lattice Gauge Theory is formulated
somewhat differently from another approach
to formulating physics models on lattices:
Feynman Checkerboards,
In the HyperDiamond Feynman Checkerboard model,
the Higgs scalar couples most strongly
with the particle-antiparticle pair
made of femions with the most charge in the highest generation.
That means Third Generation fermions made of triples of octonions,
carrying both color and electric charge, and therefore quarks
rather than leptons,
and carrying electric charge of magnitude 2/3 rather than 1/3,
and therefore:
the Higgs scalar couples most strongly with the Truth quark,
whose tree-level constituent mass of 129.5155 GeV is
somewhat lower than, but close to,
the Higgs scalar mass of about 146 GeV.
The HyperDiamond Feynman Checkerboard model value of
about 130 GeV is substantially different from
the roughly 175 GeV figure advocated by FermiLab.
I think that the FermiLab figure is incorrect.
The Fermilab figure is based on analysis of
semileptonic events. I think that the Fermilab
semileptonic analysis does not handle background correctly,
and ignores signals in the data that are in rough
agreement with the D4-D6-E6-E7 model tree level constituent mass
of about 130 GeV.
Further, I think that dileptonic events are more
reliable for Truth quark mass determination,
even though there are fewer of them than semileptonic events.
I disagree with the Fermilab D0 analysis of dileptonic events,
which Fermilab says are in the range of 168.3 GeV.
My analysis of those dileptonic events
gives a Truth quark mass of about 136.7 GeV,
in rough agreement with
the D4-D6-E6-E7 model tree level Truth quark constituent mass
of about 130 GeV.
More details about these issues,
including gif images of Fermilab data histograms
and other relevant experimental results,
can be found on the World Wide Web at URLs
http://www.innerx.net/personal/tsmith/TCZ.html
I consider the mass of the Truth quark to be
a good test of the D4-D6-E6-E7 model,
as the model is falsifiable by experimental results.
The Truth Quark, through its strong
interaction with Higgs Vacua, may have two excited energy levels at
225 GeV and 173 GeV, above a ground state at 130 GeV. The 173
GeV excited state may exist due to appearance of a Planck-energy
vaccum with < phi_vac2 > = 10^19 GeV in addition to the
low-energy Standard Model vacuum with < phi_vac1 > = 252
GeV.
Other Fermion Masses.
In the HyperDiamond Feynman Checkerboard model,
the masses of the other fermions are calculated from
the mass of the Truth quark, with the following results for
individual tree-level lepton masses and quark constituent masses:
me = 0.5110 MeV;
mnue = mnumu = mnutau = 0 at 0-level but 1-level corrections exist;
md = mu = 312.8 MeV (constituent quark mass);
mmu = 104.8 MeV;
ms = 625 MeV (constituent quark mass);
mc = 2.09 GeV (constituent quark mass);
mtau = 1.88 GeV;
mb = 5.63 GeV (constituent quark mass);
These results when added up,
with each quark having 3 color charge states,
each fermion particle having an antiparticle,
and each Dirac fermion having 2 helicity states,
give a total mass of first generation fermions:
Sigmaf1 = 7.508 GeV
Here is how the individual fermion mass calculations
are done:
The Discrete HyperDiamond Generalized
Feynman Checkerboard and Continuous
Manifolds are related by Quantum
Superposition:
The Weyl fermion neutrino has at tree level
only the left-handed state,
whereas the Dirac fermion electron and quarks can have
both left-handed and right-handed states,
so that the total number of states corresponding
to each of the half-spinor Spin(0,8) representations is 15.
In all generations, neutrinos are massless at tree level.
However, even though massless at tree level,
neutrinos are spinors and therefore are acted
upon by Gravity as shown by the Papapetrou Equations.
Further,
in Quantum Field Theory at Finite Temperature,
the gravitational equivalence principle may be violated,
causing mixing among neutrinos of different generations.
In the HyperDiamond Feynman Checkerboard model,
the first generation fermions
correspond to octonions O
and second generation fermions
correspond to pairs of octonions O x O
and third generation fermions
correspond to triples of octonions O x O x O.
To calculate the fermion masses in the model,
the volume of a compact manifold representing the
spinor fermions S8+ is used.
It is the parallelizable manifold S^7 x RP^1.
Also, since gravitation is coupled to mass,
the infinitesimal generators of the MacDowell-Mansouri
gravitation group, Spin(0,5), are relevant.
The calculated quark masses are constituent masses,
not current masses.
In the HyperDiamond Feynman Checkerboard model,
fermion masses are calculated as
a product of four factors:
V(Qfermion) x N(Graviton) x N(octonion) x Sym
V(Qfermion) is the volume of the part of
the half-spinor fermion particle manifold S^7 x RP^1
that is related to the fermion particle
by photon, weak boson, and gluon interactions.
N(Graviton) is the number of types of Spin(0,5) graviton
related to the fermion.
The 10 gravitons correspond to
the 10 infinitesimal generators of Spin(0,5) = Sp(2).
2 of them are in the Cartan subalgebra.
6 of them carry color charge,
and may therefore be considered as corresponding to quarks.
The remaining 2 carry no color charge,
but may carry electric charge
and so may be considered as corresponding to electrons.
One graviton takes the electron into itself,
and the other can only take the first-generation electron
into the massless electron neutrino.
Therefore only one graviton should correspond to the mass
of the first-generation electron.
The graviton number ratio of the down quark to the
first-generation electron is therefore 6/1 = 6.
N(octonion) is an octonion number factor relating up-type quark
masses to down-type quark masses in each generation.
Sym is an internal symmetry factor, relating 2nd and 3rd
generation massive leptons to first generation fermions.
It is not used in first-generation calculations.
The ratio of the down quark constituent mass to the electron mass
is then calculated as follows:
Consider the electron, e.
By photon, weak boson, and gluon interactions,
e can only be taken into 1, the massless neutrino.
The electron and neutrino, or their antiparticles,
cannot be combined to produce any of the
massive up or down quarks.
The neutrino, being massless at tree level,
does not add anything to the mass formula for the electron.
Since the electron cannot be related to any other massive Dirac
fermion, its volume V(Qelectron) is taken to be 1.
Next consider a red down quark I.
By gluon interactions,
I can be taken into J and K,
the blue and green down quarks.
By also using weak boson interactions,
it can be taken into i, j, and k,
the red, blue, and green up quarks.
Given the up and down quarks,
pions can be formed from quark-antiquark pairs,
and the pions can decay
to produce electrons and neutrinos.
Therefore the red down quark (similarly, any down quark)
is related to any part of S^7 x RP^1,
the compact manifold corresponding to
{ 1, i, j, k, I, J, K, E }
and therefore a down quark should have a spinor manifold
volume factor V(Qdown quark) of the volume of
S^7 x RP^1.
The ratio of the down quark spinor manifold volume factor to
the electron spinor manifold volume factor is just
V(Qdown quark) / V(Qelectron) = V(S^7x RP^1)/1 = pi^5 / 3.
Since the first generation graviton factor is 6,
md/me = 6V(S^7 x RP^1) = 2 pi^5 = 612.03937
As the up quarks correspond to i, j, and k,
which are
the octonion transforms under E of I, J, and K
of the down quarks,
the up quarks and down quarks
have the same constituent mass mu = md.
Antiparticles have the same mass as the corresponding
particles.
Since the model only gives ratios of massses,
the mass scale is fixed by assuming
that the electron mass me = 0.5110 MeV.
Then, the constituent mass of the down quark is
md = 312.75 MeV, and
the constituent mass for the up quark is
mu = 312.75 MeV.
As the proton mass is taken to be the sum of the constituent
masses of its constituent quarks
mproton = mu + mu + md = 938.25 MeV
The D4-D6-E6-E7 model calculation is close to
the experimental value of 938.27 MeV.
The third generation fermion particles correspond to triples of
octonions. There are 8^3 = 512 such triples.
The triple { 1,1,1 } corresponds to the tau-neutrino.
The other 7 triples involving only 1 and E correspond
to the tauon:
{ E, E, E },
{ E, E, 1 },
{ E, 1, E },
{ 1, E, E },
{ 1, 1, E },
{ 1, E, 1 },
{ E, 1, 1 } ,
The symmetry of the 7 tauon triples is the same
as the symmetry of
the 3 down quarks, the 3 up quarks, and the electron,
so the tauon mass should be
the same as
the sum of the masses of
the first generation massive fermion particles.
Therefore the tauon mass is 1.87704 GeV.
The calculated Tauon mass of 1.88 GeV is a sum
of first generation fermion masses, all of which are
valid at the energy level of about 1 GeV.
However, as the Tauon mass is about 2 GeV,
the effective Tauon mass should be renormalized
from the energy level of 1 GeV (where the mass is 1.88 GeV)
to the energy level of 2 GeV.
Such a renormalization should reduce the mass.
If the renormalization reduction were about 5 percent,
the effective Tauon mass at 2 GeV would be about 1.78 GeV.
The 1996 Particle Data Group Review of Particle Physics gives
a Tauon mass of 1.777 GeV.
Note that all triples corresponding to the
tau and the tau-neutrino are colorless.
The beauty quark corresponds to 21 triples.
They are triples of the same form as the 7 tauon triples,
but for 1 and I, 1 and J, and 1 and K,
which correspond to the red, green, and blue beauty quarks,
respectively.
The seven triples of the red beauty quark correspond
to the seven triples of the tauon,
except that the beauty quark interacts with 6 Spin(0,5)
gravitons while the tauon interacts with only two.
The beauty quark constituent mass should be the tauon mass times the
third generation graviton factor 6/2 = 3, so the B-quark mass is
mb = 5.63111 GeV.
The calculated Beauty Quark mass of 5.63 GeV is a
consitituent mass, that is,
it corresponds to the conventional pole mass plus 312.8 MeV.
Therefore, the calculated Beauty Quark mass of 5.63 GeV
corresponds to a conventional pole mass of 5.32 GeV.
The 1996 Particle Data Group Review of Particle Physics gives
a lattice gauge theory Beauty Quark pole mass as 5.0 GeV.
The pole mass can be converted to an MSbar mass
if the color force strength constant alpha_s is known.
The conventional value of alpha_s at about 5 GeV is about 0.22.
Using alpha_s (5 GeV) = 0.22,
a pole mass of 5.0 GeV gives an MSbar 1-loop mass of 4.6 GeV,
and an MSbar 1,2-loop mass of 4.3, evaluated at about 5 GeV.
If the MSbar mass is run from 5 GeV up to 90 GeV,
the MSbar mass decreases by about 1.3 GeV,
giving an expected MSbar mass of about 3.0 GeV at 90 GeV.
DELPHI at LEP has observed the Beauty Quark
and found a 90 GeV MSbar mass of about 2.67 GeV,
with error bars +/- 0.25 (stat) +/- 0.34 (frag) +/- 0.27 (theo).
Note that the D4-D6-E6-E7 model calculated mass of 5.63 GeV
corresponds to a pole mass of 5.32 GeV,
which is somewhat higher than the conventional value of 5.0 GeV.
However,
the D4-D6-E6-E7 model calculated value of
the color force strength constant alpha_s at
about 5 GeV is about 0.166,
while
the conventional value of
the color force strength constant alpha_s at
about 5 GeV is about 0.216,
and
the D4-D6-E6-E7 model calculated value of
the color force strength constant alpha_s at
about 90 GeV is about 0.106,
while
the conventional value of
the color force strength constant alpha_s at
about 90 GeV is about 0.118.
The D4-D6-E6-E7 model calculations gives
a Beauty Quark pole mass (5.3 GeV)
that is about 6 percent higher
than the conventional Beauty Quark pole mass (5.0 GeV),
and
a color force strength alpha_s at 5 GeV (0.166) such that
1 + alpha_s = 1.166 is about 4 percent lower
than the conventional value of 1 + alpha_s = 1.216 at 5 GeV.
Note particularly that triples of the type { 1, I, J },
{ I, J, K }, etc.,
do not correspond to the beauty quark, but to the truth quark.
The truth quark corresponds to the remaining 483 triples, so the
constituent mass of the red truth quark is 161/7 = 23 times the
red beauty quark mass, and the red T-quark mass is
mt = 129.5155 GeV
The blue and green truth quarks are defined similarly.
All other masses than the electron mass
(which is the basis of the assumption of the value of the
Higgs scalar field vacuum expectation value v = 252.514 GeV),
including the Higgs scalar mass and Truth quark mass,
are calculated (not assumed) masses in the HyperDiamond Feynman
Checkerboard model.
The tree level T-quark constituent mass rounds off to 130 GeV.
These results when added up give a total mass of
third generation fermions:
Sigmaf3 = 1,629 GeV
The second generation fermion calculations are:
The second generation fermion particles correspond
to pairs of octonions.
There are 8^2 = 64 such pairs.
The pair { 1,1 } corresponds to the mu-neutrino.
the pairs { 1, E }, { E, 1 }, and
{ E, E } correspond to the muon.
Compare the symmetries of the muon pairs to the symmetries
of the first generation fermion particles.
The pair { E, E } should correspond
to the E electron.
The other two muon pairs have a symmetry group S2,
which is 1/3 the size of the color symmetry group S3
which gives the up and down quarks their mass of 312.75 MeV.
Therefore the mass of the muon should be the sum of
the { E, E } electron mass and
the { 1, E }, { E, 1 } symmetry mass,
which is 1/3 of the up or down quark mass.
Therefore, mmu = 104.76 MeV.
According to the 1998 Review of
Particle Physics of the Particle Data Group, the experimental
muon mass is about 105.66 MeV.
Note that all pairs corresponding to
the muon and the mu-neutrino are colorless.
The red, blue and green strange quark each corresponds
to the 3 pairs involving 1 and I, J, or K.
The red strange quark is defined as the thrge pairs
1 and I, because I is the red down quark.
Its mass should be the sum of two parts:
the { I, I } red down quark mass, 312.75 MeV, and
the product of the symmetry part of the muon mass, 104.25 MeV,
times the graviton factor.
Unlike the first generation situation,
massive second and third generation leptons can be taken,
by both of the colorless gravitons that
may carry electric charge, into massive particles.
Therefore the graviton factor for the second and
third generations is 6/2 = 3.
Therefore the symmetry part of the muon mass times
the graviton factor 3 is 312.75 MeV,
and
the red strange quark constituent mass
is
ms = 312.75 MeV + 312.75 MeV = 625.5 MeV
The blue strange quarks correspond to the
three pairs involving J,
the green strange quarks correspond to the
three pairs involving K,
and their masses are determined similarly.
The charm quark corresponds to the other 51 pairs.
Therefore, the mass of the red charm quark should
be the sum of two parts:
the { i, i }, red up quark mass, 312.75 MeV; and
the product of the symmetry part of the strange quark
mass, 312.75 MeV, and
the charm to strange octonion number factor 51/9,
which product is 1,772.25 MeV.
Therefore the red charm quark constituent mass
is
mc = 312.75 MeV + 1,772.25 MeV = 2.085 GeV
The blue and green charm quarks are defined similarly,
and their masses are calculated similarly.
The calculated Charm Quark mass of 2.09 GeV is a
consitituent mass, that is,
it corresponds to the conventional pole mass plus 312.8 MeV.
Therefore, the calculated Charm Quark mass of 2.09 GeV
corresponds to a conventional pole mass of 1.78 GeV.
The 1996 Particle Data Group Review of Particle Physics gives
a range for the Charm Quark pole mass from 1.2 to 1.9 GeV.
The pole mass can be converted to an MSbar mass
if the color force strength constant alpha_s is known.
The conventional value of alpha_s at about 2 GeV is about 0.39,
which is somewhat lower than the D4-D6-E6-E7 model value.
Using alpha_s (2 GeV) = 0.39,
a pole mass of 1.9 GeV gives an MSbar 1-loop mass of 1.6 GeV,
evaluated at about 2 GeV.
These results when added up give a total mass of
second generation fermions:
Sigmaf2 = 32.9 GeV
K-M Parameters.
The Kobayashi-Maskawa parameters are determined in terms of
the sum of the masses of the 30 first-generation
fermion particles and antiparticles, denoted by Smf1 = 7.508 GeV,
and
the similar sums for second-generation and third-generation fermions,
denoted by Smf2 = 32.94504 GeV and Smf3 = 1,629.2675 GeV.
The reason for using sums of all fermion masses
(rather than sums of quark masses only) is that
all fermions are in the same spinor representation of Spin(8),
and the Spin(8) representations are considered to be fundamental.
The following formulas use the above masses to
calculate Kobayashi-Maskawa parameters:
phase angle d13 = 1 radian ( unit length on a phase circumference )
sin(alpha) = s12 =
= [me+3md+3mu]/sqrt([me^2+3md^2+3mu^2]+[mmu^2+3ms^2+3mc^2]) =
= 0.222198
sin(beta) = s13 =
= [me+3md+3mu]/sqrt([me^2+3md^2+3mu^2]+[mtau^2+3mb^2+3mt^2])=
= 0.004608
sin(*gamma) =
= [mmu+3ms+3mc]/sqrt([mtau^2+3mb^2+3mt^2]+[mmu^2+3ms^2+3mc^2])
sin(gamma) = s23 = sin(*gamma) sqrt( Sigmaf2 / Sigmaf1 ) =
= 0.04234886
The factor sqrt( Smf2 /Smf1 ) appears in s23 because
an s23 transition is to the second generation and
not all the way to the first generation,
so that the end product of an s23 transition has a
greater available energy than s12 or s13 transitions
by a factor of Smf2 / Smf1 .
Since the width of a transition is proportional to
the square of the modulus of the relevant KM entry and
the width of an s23 transition has greater available energy
than the s12 or s13 transitions by a factor of Smf2 / Smf1
the effective magnitude of the s23 terms in the KM entries
is increased by the factor sqrt( Smf2 /Smf1 ) .
The Chau-Keung parameterization is used,
as it allows the K-M matrix to be represented as
the product of the following three 3x3 matrices:
1 0 0
0 cos(gamma) sin(gamma)
0 -sin(gamma) cos(gamma)
cos(beta) 0 sin(beta)exp(-i d13)
0 1 0
-sin(beta)exp(i d13) 0 cos(beta)
cos(alpha) sin(alpha) 0
-sin(alpha) cos(alpha) 0
0 0 1
The resulting Kobayashi-Maskawa parameters
for W+ and W- charged weak boson processes, are:
d s b
u 0.975 0.222 0.00249 -0.00388i
c -0.222 -0.000161i 0.974 -0.0000365i 0.0423
t 0.00698 -0.00378i -0.0418 -0.00086i 0.999
The matrix is labelled by either
(u c t) input and (d s b) output,
or, as above,
(d s b) input and (u c t) output.
For Z0 neutral weak boson processes, which are suppressed
by the GIM mechanism of cancellation of virtual subprocesses,
the matrix is labelled by either
(u c t) input and (u'c't') output,
or, as below,
(d s b) input and (d's'b') output:
d s b
d' 0.975 0.222 0.00249 -0.00388i
s' -0.222 -0.000161i 0.974 -0.0000365i 0.0423
b' 0.00698 -0.00378i -0.0418 -0.00086i 0.999
Since neutrinos of all three generations are massless at tree level,
the lepton sector has no tree-level K-M mixing.
According to a
Review on the KM mixing matrix by Gilman, Kleinknecht, and Renk in
the 2002 Review of Particle Physics:
"... Using the eight tree-level constraints discussed below
together with unitarity, and assuming only three generations, the 90%
confidence limits on the magnitude of the elements of the complete
matrix are
d s b
u 0.9741 to 0.9756 0.219 to 0.226 0.00425 to 0.0048
c 0.219 to 0.226 0.9732 to 0.9748 0.038 to 0.044
t 0.004 to 0.014 0.037 to 0.044 0.9990 to 0.9993
... The constraints of unitarity connect different elements, so
choosing a specific value for one element restricts the range of
others. ... The phase d13 lies in the range 0 < d13 < 2 pi,
with non-zero values generally breaking CP invariance for the weak
interactions. ... Using tree-level processes as constraints only, the
matrix elements ...[ of the 90% confidence limit shown above
]... correspond to values of the sines of the angles of s12 =
0.2229 +/- 0.0022, s23 = 0.0412 +/- 0.0020, and s13 = 0.0036 +/-
0.0007. If we use the loop-level processes discussed below as
additional constraints, the sines of the angles remain unaffected,
and the CKM phase, sometimes referred to as the angle gamma = phi3 of
the unitarity triangle ...
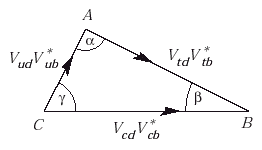
... is restricted to d13 = ( 1.02 +/- 0.22 ) radians = 59 +/- 13
degrees. ... CP-violating amplitudes or differences of rates are all
proportional to the product of CKM factors ... s12 s13 s23 c12 c13^2
c23 sind13. This is just twice the area of the unitarity triangle.
... All processes can be quantitatively understood by one value of
the CKM phase d13 = 59 +/- 13 degrees. The value of beta = 24 +/- 4
degrees from the overall fit is consistent with the value from the
CP-asymmetry measurements of 26 +/- 4 degrees. The invariant measure
of CP violation is J = ( 3.0 +/- 0.3) x 10^(-5). ... From a combined
fit using the direct measurements, B mixing, epsilon, and sin2beta,
we obtain: Re Vtd = 0.0071 +/- 0.0008 , Im Vtd = -0.0032 +/- 0.0004
... Constraints... on the position of the apex of the unitarity
triangle following from | Vub | , B mixing, epsilon, and sin2beta.
...
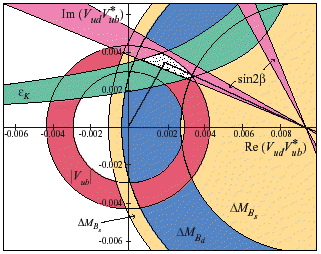
... A possible unitarity triangle is shown with the apex in the
preferred region. ...".
In hep-ph/0208080,
Yosef Nir says: "... Within the Standard Model, the only source of CP
violation is the Kobayashi-Maskawa (KM) phase ... The study of CP
violation is, at last, experiment driven. ... The CKM matrix provides
a consistent picture of all the measured flavor and CP violating
processes. ... There is no signal of new flavor physics. ... Very
likely, the KM mechanism is the dominant source of CP violation in
flavor changing processes. ... The result is consistent with the SM
predictions. ...".
In hep-ph/0304132,
Marco Battaglia says: "... This ... 330 page ... report contains
the results of the Workshop on the CKM Unitarity Triangle, held at
CERN on 13-16 February 2002 to study the determination of the CKM
matrix from the available data of K, D, and B physics. This is a
coherent document with chapters covering the determination of CKM
elements from tree level decays and K and B meson mixing and the
global fits of the unitarity triangle parameters. The impact of
future measurements is also discussed. ...".
D. L. Khokhlov,
in hep-ph/9809457, describes muon decay by 2-photon processes and
tauon decay by 3-photon processes, a picture that is consistent with
the D4-D6-E6-E7 physics model which
describes
Since a muon would look like a pair of octonions, it should decay
by a 2-photon process.
Khokhlov refers to Quantum Electrodynamics by Landau and Lifshitz
(3rd ed, Nauka, 1989), for the 2-photon scattering cross section
sigma_2, for the energy level hbar omega = m_e c^2 at which formation
of real electron-positron pairs becomes possible,
sigma_2 = 0.031 alpha^2 r_cl^2
where alpha is the electromagnetic fine structure constant, r_cl =
e^2 / m_e c^2 is the classical electron radius, omega is frequencey,
hbar is Planck's constant h divided by 2 pi, c is the speed of light,
and m_e is the electron mass.
As the effective radius r_2 of 2-photon scattering is given by r_2
= sqrt( sigma_2 / pi )
r_2 = sqrt( 0.031 alpha^2 r_cl^2 / pi ) = ( 1 / 137 ) sqrt (
0.031 / pi ) 2.8 x 10^(-13) cm =
= 2 x 10^(-16) cm
Since the Compton wavelength r_e of an electron is about 3.86 x
10^(-11) cm, and the electron mass/energy m_e is about 0.511 MeV, the
energy level corresponding to muon 2-photon decay is 1.93 x 10^5 m_e
= 98.6 GeV, which is the same order as the mass/energy of W-bosons
(about 80 GeV) that mediate muon decay in the D4-D6-E6-E7
physics model and the Standard Model
muon
to
mu-neutrino + W
to
mu-neutrino + electron + e-antineutrino
Since 2-photon processes are characterized by the classical
electron radius r_cl, the muon mass M_mu should be of the order
M_mu = hbar / c r_cl = ( r_e / r_cl ) 0.511 MeV =
= ( 3.86 x 10^(-11) / 2.8 x 10^(-13) ) 0.511 MeV = 70
MeV
which is the same order as the experimental muon mass 105.66 MeV
and the D4-D6-E6-E7 model
calculated tree-level muon mass 104.8
MeV.
Since 3-photon processes are characterized by the triplet state of
positronium, and 2-photon processes are characterized by the singlet
state of positronium, and, according to Sakurai (Advanced Quantum
Mechanics, Addison-Wesley 1967, page 227), for the n =1, s wave bound
states of positronium, the lifetime ratio T_singlet / T_triplet = 9
pi / 4 ( pi^2 - 9 ) alpha = 1115, the tauon mass M_tau should be of
the order
M_tau = M_mu sqrt( T_singlet / T_triplet ) = 2300
MeV
which is the same order as the experimental tauon mass 1777 MeV,
the D4-D6-E6-E7 model
calculated tree-level tauon mass 1877 MeV,
and the tauon mass estimate of Khokhlov of 2200 MeV.
From Sets to Quarks:
Table of Contents:
Chapter 1 - Introduction.
Chapter 2 - From Sets to Clifford Algebras.
Chapter 3 - Octonions and E8 lattices.
Chapter 4 - E8 spacetime and particles.
Chapter 5 - HyperDiamond Lattices.
Chapter 6 - Spacetime and Internal Symmetry Space.
Chapter 7 - Feynman Checkerboards.
Chapter 8 - Charge = Amplitude to Emit Gauge Boson.
Chapter 9 - Mass = Amplitude to Change Direction.
Chapter 10 - Protons, Pions, and Physical Gravitons.
Appendix A - Errata for Earlier Papers.
References.
Tony Smith's Home Page
......

 ...
...
 ...".
...".


