The Discrete HyperDiamond Generalized Feynman Checkerboard and Continuous Manifolds are related by Quantum Superposition:
Dimensional reduction reduces the original nonassociative octonionic 8-dimensional Spacetime to a physical associative 4-dimensional Spacetime and a coassociative 4-dimensional Internal Symmetry Space. It also reduces the 28 gauge bosons of Spin(8) to 16 generators of the Lie Algebra U(4) = U(1)xSU(4) = U(1)xSpin(6) of Gravity and the Higgs Mechanism plus 12 generators of the Lie Algebra U(1)xSU(2)xSU(3) of the Standard Model.
The D4-D5-E6-E7-E8 VoDou Physics model Lagrangian action, after dimensional reduction, is the sum of 4 terms:
Int Lgr dMgr + Int Lsu3 dMsu3 + Int Lsu2 dMsu2 + Int Lu1 dMu1
where Int stands for integration,
Lgr, Lsu3, Lsu2, and Lu1 are Lagrangian densities for the gravity, color, weak, and electromagnetic forces, and
dMgr, dMsu3, dMsu2, and dMu1 are the integration volume elements for the gravity, color, weak, and electromagnetic forces.
The integration Int is taken over a neighborhood M of 4-dimensional spacetime. By Wick rotation, M can be seen as either Euclidean or Minkowski.
The Lagrangian terms for gravity, the SU(3) color force, the SU(2) weak force, and U(1) electromagnetism each determine the geometric force strength constants for their respective forces. The gauge boson curvature part of the relative geometric force strengths (not including 1/mass squared terms for the Fermi weak constant and for the Newton gravitational constant) can be calculated by looking at the gauge boson curvature terms of the form F /\ *F for
Lgr, Lsu3, Lsu2, and Lu1,
and comparing the measures dMgr, dMsu3, dMsu2, and dMu1 ,
each measure being defined by the volume of a 4-dimensional compact symmetric space of constant curvature.
The compact spaces of constant curvature are defined by transitive action of each of the 4 forces on its respective 4-dimensional Symmetry Space (for the SU(3) color, SU(2) weak, and U(1) electromagnetic forces, the coassociative Internal Symmetry Space; and for Gravity, Spacetime),
that is, by the way the gauge bosons "see" their Symmetry Space:
Denote the 4 Symmetry Space components of the gauge boson by:
The Discrete HyperDiamond Generalized Feynman Checkerboard and Continuous Manifolds are related by Quantum Superposition:
Note that S1/Z2 can be described as an orbifold.
Dimensional reduction reduces the original nonassociative octonionic 8-dimensional Spacetime to a physical associative 4-dimensional Spacetime and a coassociative 4-dimensional Internal Symmetry Space. It also reduces the 28 gauge bosons of Spin(8) to 16 generators of the Lie Algebra U(4) = U(1)xSU(4) = U(1)xSpin(6) of Gravity and the Higgs Mechanism plus 12 generators of the Lie Algebra U(1)xSU(2)xSU(3) of the Standard Model.
Corresponding to the way that 24 of the 28 Gauge Bosons of the D4-D5-E6-E7-E8 VoDou Physics model can be represented by the vertices of a 24-cell, SpaceTime plus Internal Symmetry Space, and the first-generation Fermion Particles and anti-Particles, can be represented by the vertices of a dual 24-cell:
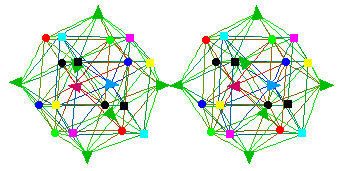
In the dual 24-cell, 8-dimensional spacetime is represented by 8 vertices that correspond, after dimensional reduction, to
In this image
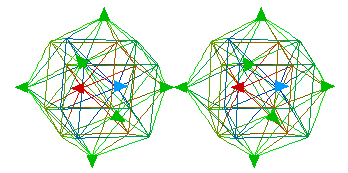
only the 8 vertices representing Physical SpaceTime and Internal Symmetry Space are marked.
Matti Pitkanen has suggested that the global structure of 4-dimensional Spacetime and Internal Symmetry Space should be given by 8-dimensional SU(3), which decomposes by SU(3) / U(2) = CP2 into CP2 base and U(2) fibre, both of which are 4-dimensional and have Quaternionic structure.
Associative 4-dimensional Spacetime, in the Minkowski version with -+++ signature (1,3), is topologically U(2) = SU(2)xU(1) = S3 x S1 (while the Euclidean version of Spacetime has topology S4),
which is consistent with the D4-D5-E6-E7-E8 VoDou Phyiscs model Spacetime of RP1 x S3. As Matti Pitkanen has noted, the Quaternions have both a natural Minkowski metric (given by the square root of the real part Re(ZZ) of Z times Z for Quaternion Z) and a natural Euclidean metric (given by the square root of ZZ* of Z times Z conjugate for Quaternion Z).
Coassociative 4-dimensional Internal Symmetry Space is CP2.
What is the relationship between 8-dimensional SU(3) and 8-dimensional Octonions?
However, 1^2 = 1 and E^2 = -1, so 1 and E are not isomorphic,so the Octonion {1,E} is not isomorphic to the SU(3) Cartan subalgebra.
Also, Octonion {i,j,k} is not isomorphic to {I,J,K}, but SU(3) 3-dim representation is isomorphic to the dual 3-dim rep.
So, SU(3) and Octonions have their differences.
Look at the automorphism group Aut(O) = G2 of the Octonions.
Unlike the Quaternion case, where Aut(Q) = SU(2) = Spin(3) = S3 = Imaginary Quaternions, Aut(O) = G2 is 14-dimensional, whereas S7 = Imaginary Octonions is 7-dim.
Also unlike the Quaternion case, where SU(2) = Spin(3) double-covers the rotation group in 3-space, Aut(O) = G2 is not Spin(7) and is not the double-cover of the rotation group in 7-space, but Spin(7) and G2 are related by Spin(7) / G2 = S7.
How does Aut(O) = G2 act on 7-space?
Look at the 6-sphere S6 in 7-space.
Aut(O) = G2 is transitive on S6, just as is the double-cover Spin(7) of the rotation group in 7-space, but the isotropy group of the double-cover Spin(7) of the rotation group in 7-space is Spin(6),
that is, Spin(7) / Spin(6) = S6,
whereas Spin(7) / G2 = S7 and Spin(6) / SU(3) = S7
and the isotropy group of G2 is SU(3), that is, G2 / SU(3) = S6.
The elements of SU(3) are automorphisms of the Octonions and SU(3) is a subgroup of Spin(6) = SU(4), by the fibration Spin(6) / U(3) = SU(4) / (SU(3)xU(1)) = SU(4) / U(3) = CP3.
What does SU(4) look like? Consider the exterior algebra graded structures:
1 + 4 + 6 + 4 + 1 SU(4) has 4 and 4 irreps 1 + 3 + 3 + 1 SU(3) has 3 and 3 irreps
The 8-dimensional adjoint rep of SU(3) is 3x3 - 1 = 9-1 = 8 dim, and can be mapped to a 1+3+3+1 = 8 dim representation of full exterior algebra, and therefore can be mapped to the sum of the 4 and 4 irreps of SU(4). (This map may not be an isomorphism but it is a nice 1-1 homeomorphism of the representation vector spaces.)
How are the 4 and 4 irreps of SU(4) related to the Octonions? Look at Spin(6) = SU(4). Spin(6) is based on the Clifford Algebra Cl(0,6):
1 + 6 + 15 + 20 + 15 + 6 + 1 = 2^6 = 64 = 8x8
rows------------> c x x x x x x x x o x x x x x x x x l x x x x x x x x u x x x x x x x x m n x x x x x x x x s x x x x x x x x | x x x x x x x x \ / x x x x x x x x
The 1x8 rows of the 8x8 matrices of Cl(0,6) are the full spinor minimal ideals, and each 1x4 and 1x4 half-row is an irreducible half-spinor minimal ideal of Cl(0,6). Each 4-dim half-row half-spinor rep of Spin(6) is isomorphic to one of 4-dim reps of SU(4). Taken together, the two 4-dim half-spinor reps of Spin(6) form its 8-dim full spinor rep.
When you embed Cl(0,6) in Cl(0,7), the 8-dim reducible full spinor rep of Spin(6) is mapped to the 8-dim irreducible spinor rep of Spin(7), which is isomorphic to the 8-dim Octonions.
All this does not give an isomorphism of the algebra of Octonions with the global group structure of SU(3), but it does give a homeomorphism between the 8-dim vector space of the Octonions and the 8-dim vector space of the SU(3) Lie Algebra (NOT the global SU(3) Lie Group).
The 8-dim spacetime Octonion vector space reduces to 4-dim physical Spacetime and 4-dim Internal Symmetry Space, and the vector space identification with SU(3) indicates that
the topology of the Minkowski version of Spacetime should be S1 x S3 (the same topology as RP1 x S3) (while the Euclidean version of Spacetime has topology S4),
and
the topology of Internal Symmetry Space should be CP2.
Since RP1xS3 is the Shilov boundary of the bounded complex homogeneous domain corresponding to the symmetric space Spin(2,4) / Spin(2)xSpin(4), where Spin(2,4) is the Conformal group of 4-dim Minkowski spacetime, if you regard Physical SpaceTime as the 6-dimensional vector space of Spin(2,4), and Internal Symmetry Space as 5-dimensional CP2, then the total space is 6+4=10-dimensional with signature (2,8). With respect to the D4-D5-E6-E7-E8 VoDou Physics model, that 10-dim space corresponds:to the 10-dim vector space of the D5 Lie Algebra Spin(2,8); andto the 10-dim element of the decomposition of the 27-dim representation of the E6 Lie Algebra into 10 + 16 + 1 under its D5 subalgebra (see, for example, Lie Algebras in Particle Physics, 2nd edition, by Howard Georgi, Perseus Books (1999), page 308).
The (1,7)-dimensional RP1 x S7 = S1 x S7 = U(1) x S7 spacetime of the D4-D5-E6-E7-E8 VoDou Physics model prior to dimensional reduction can be represented by Quaternionic Projective 2-space QP2.
As Atiyah and Berndt say in their paper Projective Planes, Serveri Varieties, and Spheres, math.DG/0206135, the S1 x S7 considered as QP2 breaks down into two parts:
Here are some excerpts from the paper by Atiyah and Berndt entitled Projective Planes, Serveri Varieties, and Spheres, math.DG/0206135, where they denote Quaternions by H rather than the Q that I usually use: "... There are natural diffeomorphisms
- CP2 / O(1) = S4 ... S0 = O(1) ...
- HP2 / U(1) = S7 ... S1 = U(1) ...
- OP2 / Sp(1) = S13 ... S3 = Sp(1) ...
... The maps from the projective planes to the spheres ... are fibrations outside the "branch locus" given by the preceding projective plane. ... The embeddings of the branch loci
RP2 in S4 , CP2 in S7 , HP2 in S13 ... If we denote the projective planes by Pn (n=0,1,2,3), so that dim Pn = 2^(n+1), then their complexifications Pn(C) are complex algebraic varieties of complex dimension 2^(n+1). ... The compact complex manifolds Pn(C) are ...
- P0(C) = SU(3) / S(U(1)xU(2)) = CP2
- P1(C) = SU(3)^2 / S(U(1)xU(2))^2 = CP2 x CP2
- P2(C) = SU(6) / S(U(2)xU(4)) = Gr2(C6)
- P3(C) = E6 / Spin(10)xU(1)
... The isometry group of Pn extends to an action of its complexification on Pn(C) leaving invariant a complex hypersurface Pn(oo). Moreover, Pn(C) has a "real structure", i.e. a complex conjugation. The real points are just Pn , and Pn(oo) inherits a real structure with no real points. ...
... when n = 1 ... P1(oo) ... with fibre L1(oo) ... is the twistor fibration for CP2 regarded as a 4-manifold with self-dual metric ... For n = 2,3 the fibration is a partial twistor fibration ...
- P2(oo) = Sp(3) / Sp(1)U(2) -> Sp(3) / Sp(1)Sp(2) = HP2 ... fibre ... L2(oo) = Sp(2) / U(2) ...
- P3(oo) = F4 / Spin(7)U(1) -> F4 / Spin(9) = OP2 ... fibre ... L3(oo) = Spin(9) / Spin(7)U(1) ...
... For each n = 0,1,2,3 we have a natural map
PSn : Pn(C) -> S(d(n)) , d(n) = 3 x 2^n + 1 ...[i.e.
- PS0 : P0(C) -> S4
- PS1 : P1(C) -> S7
- PS2 : Pn(C) -> S13
- PS3 : P3(C) -> S25
]... which is a fibration outside the branch locus Pn and the hypersurface Pn(oo). The fibres are the spheres S0, S1, S3, S7. ... the complexification of CP2 is just the product CP2 x CP2, while ... the complexification of HP2 turns out to be the complex Grassmannnian Gr2(C6) of 2-planes in C6 ... and ... the complexification of OP2 is the exceptional Hermitian symmetric space E6 / Spin(10)xU(1) ...
... denote by Gn the groups of isometries of Pn ... namely
- G0 = SO(3)
- G1 = SU(3)
- G2 = Sp(3)
- G3 = F4
... The space Hn of Hermitian ..[3x3]... matrices is a representation of Gn , which splits off a trivial factor (corresponding to the trace). ... Pn is contained in Hn , the space of Hermitian 3x3 matrices over the division algebra An . It is the orbit of the diagonal matrix Diag(1,0,0) under the compact Lie group Gn ... Note that Pn is contained in Hn(1) , the affine subspace of matrices of trace one. ... the real projective space of the vector space Hn ...[has dimension]... 3 x 2^n +2 ... the generic orbit of the action of Gn on Pn(C) has codimension one ... the generic orbits are
- n = 0 : SO(3) / O(1)
- n = 1 : SU(3) / U(1)
- n = 2 : Sp(3) / Sp(1) x Sp(1)
- n = 3 : F4 / Spin(7) ... this follows from ... S15 = Spin(9) / Spin(7) ...
... consider ... the action of SU(3) on HP2 via the embedding SU(3) in Sp(3) , and on S7 as the unit sphere in the vector space of Hermitian 3x3 complex matrices of trace zero equipped with its usual norm. For S7 we find two copies of CP2 as special orbits and the complex flag manifold of all full flags in C3 as generic orbit ... For HP2 the two special orbits are CP2 and a circle bundle over the dual CP2 which is a 5-dimensional sphere S5 (as one sees by using all quaternion lines, i.e. 4-spheres, determined by complex lines). ...[There is]... a map HP2 -> S7 compatible with the two SU(3) actions. It identifies the CP2 in HP2 with one of the two CP2 in S7 , and on the complement HP2 \ CP2 it is an S1 bundle over the complement S7 \ CP2 . The SU(3) determines a maximal subgroup U(3) of Sp(3) , and the central U(1) in this U(3) acts trivially on the CP2 and gives the fibres on HP2 \ CP2 . ...
... Wallach proved that the only simply connected closed smooth manifolds admitting a homogeneous Riemannian metric with positive sectional curvature are ...
- ... the even-dimensional spheres
- ... the projective spaces CPm , HPm , and OP2 (m > 2)
- ... the flag manifolds
- SU(3) / U(1)^2 ... of all full flags in CP2 ...
- Sp(3) / Sp(1)^3 ... of all full flags in ... HP2 ...
- F4 / Spin(8) ... of all full flags in ... OP2 ...
However, we shold point out that the positive curvature metrics on these flag manifolds are not the induced metrics from the spheres with their standard metrics. ...
... Now we shall extend these results ... to the non-compact groups ... of projectivities of Pn. ... we have a cubic polynomial det in Hn whose vanishing defines a hypersurface Zn ...[in].... the real projective space associated with Hn ... Consider ... the projective lines of Pn ...[to get a]... picture of the geometry of Zn in relation to Pn. ... any line in Pn ... is a sphere of dimension 2^n ... For a fixed line in Pn the geometry of its interior is just hyperbolic geometry and the subgroup of ... projectivities ... preserving the line is the conformal group of the sphere or the isometry group of its interior. ... ".
Since Gauge Bosons can be represented as AntiSymmetric Pairs of Fermion Nearest-Neighbors, consistently with
Since n (n-1) / 2 is the dimension of grade-2 Gauge Boson Bivectors of a Clifford Algebra Cl(n), and
since, by Triality, for the Cl(8) Clifford Algebra of the D4-D5-E6-E7-E8-E8 VoDou Physics model the dimension 8 of the half-spinor representation space of the Fermion Particles, and hence the number 8 of the Fermion Particles prior to dimensional reduction, is equal to the number 8 of Fermion AntiParticles, and to the dimension 8 of unreduced vector SpaceTime:
Since gluons can carry {+r,-r;+g,-g;+b,-b} charge, a gluon can emit three pairs: {+r,-r};{+g,-g};{+b,-b}.
As a gluon can emit three pairs, it can enlarge its path of transitive action in Internal Symmetry Space to 4 dimensions. Therefore, gluon boundary conditions are the same all around the boundary. Since SU(3) is complex, the corresponding compact space of constant curvature is complex projective 2-space CP2:
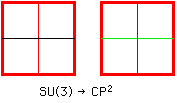
CP2 Internal Symmetry Space is a nice space on which SU(3) acts globally,
( Global Group Structure of the Standard Model is discussed here.)
The global nature of the color force SU(3) action on CP2 is related to the nature of a gluon as a link with both spacetime and color internal symmetry space characteristics, which requires gluon confinement within protons, pions, and other particles containing them.
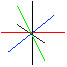
Since weak bosons can carry {+1,-1} charge, a weak boson can emit a {+1,-1} pair.
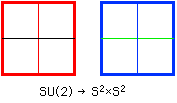
As a weak boson can emit a pair, it can enlarge its path of transitive action in Internal Symmetry Space to 2 dimensions. Therefore, weak boson boundary conditions form two 2-spheres:
Since CPn = Cn u CP(n-1) (where u = union, by putting a CP(n-1) at infinity),
CP2 = C2 u C1 u C0 = C2 u CP1 = C2 u S2.
Therefore, CP2 Internal Symmetry Space contains a 2-sphere S2 on which SU(2) can act globally,
since SU(2) / U(1) = S2.
A second copy of S2 is necessary to get a 4-dimensional manifold S2xS2.
The second copy of S2 can live in the C2 of CP2 = C2 u C1 u C0 = C2 u S2.
In the C2 of CP2 = C2 u S2, the C2 contains a copy of S2 that is linearly independent of the S2.
The local nature of the weak force SU(2) action on CP2 is related to the nature of weak bosons as having only internal symmetry space characteristics.
The mass factor for the weak force has a visualization (arising from e-mail discussion with Dick Andersen). Gauge bosons are visualized as going from a source through a medium to a target. The weak force mass factor is related to the Higgs mechanism. The Higgs scalar field absorbs some of the weak bosons as they go through the medium, thus weakening the weak force and producing the weaker effective weak force that is observed by experiments;
Since all photons have no charge, a photon can only move along its path of transitive action in Internal Symmetry Space.
As a photon cannot emit another photon, it cannot enlarge its path of transitive action in Internal Symmetry Space beyond the 1 dimension of the path of transitive action in Internal Symmetry Space. Therefore, photon boundary conditions form a 4-torus, or four 1-spheres:
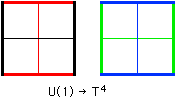
Since CPn = Cn u CP(n-1) (where u = union, by putting a CP(n-1) at infinity), and CP0 = C0 = {point},
CP2 = C2 u C1 u C0.
Since C1 contains the unit circle S1 = U(1),
U(1) has a natural action on a part of CP2 Internal Symmetry Space.
Three more copies of S1 are necessary to get a 4-dimensional manifold S1xS1xS1xS1 = T4.
In the C2 of CP2 = C2 u C1 u C0, the C2 contains three copies of S1 that are linearly independent of each other and of the S1 that is the unit circle in the C1.
The local nature of the electromagnetic U(1) action on CP2 is related to the nature of photons as having only internal symmetry space characteristics.
Since gravitons can carry {+1,-1;+r,-r;+g,-g;+b,-b} charge, a graviton can emit four pairs: {+1,-1};{+r,-r};{+g,-g};{+b,-b}.
As a graviton can emit at least three pairs, it can enlarge its path of transitive action in its Symmetry Space to 4 dimensions. Therefore, graviton boundary conditions are the same all around the boundary. Spin(5), a compact Lie group corresponding to Spin(2,3), acts globally on a compact space of constant curvature, a 4-sphere = S4 = Spin(5)/Spin(4), the Euclidean version of Spacetime ( the non-compact Minkowski version on which Spin(2,3) acts being RP1xS3 ):
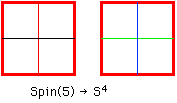
Unlike the other 3 forces that act transitively on the coassociative Internal Symmetry Space, gravity comes from the U(4) subgroup of Spin(8) and therefore acts transitively on the associative physical spacetime.
By the emission of four pairs, a graviton can describe the structure of a 4-dimensional spacetime.
A 4-pair graviton emission is effectively creation of a virtual 1-vertex spacetime Planck mass black hole.
The mass factor for gravitation has a visualization (arising from e-mail discussion with Dick Andersen). Gauge bosons are visualized as going from a source through a medium to a target. The graviton by itself is long-range and massless, but virtual Planck-mass black holes in spacetime absorb some of the gravitons as they go through the spacetime medium, thus weakening the gravitational force and producing the weaker effective gravitational force that is observed by experiments;
If the space and time axes of the 1-vertex black hole become connected with the space and time axes of the original spacetime, then the virtual Planck-mass black hole acts to provide the mass factor (1/MPlanck^2) for the force strength of low-energy effective gravitation in the D4-D5-E6-E7-E8 model.
4-pair graviton interactions are important in the Many Worlds Quantum Theory of the D4-D5-E6-E7-E8 model.
Virtual Gravitons might allow communication between a Parent Universe and a New Universe created at a vertex of the Parent Universe by a Cosmological Instanton.
Quantum fluctuations of new spacetime creation may interchange time and space axes, creating a new spacetime with lightcones tilted with respect to the original spacetime. The new tilted spacetime then has its own lightcone and conformal symmetry. For an illustration of tilted lightcones, see the lightcones in Duchamp's The Large Glass.
The tilted lightcone spacetimes probably constitute a very small part of any quantum superposition describing physical spacetime, so that conformal symmetry and preservation of lightcone structure is probably a good enough approximation to use quantum conformal fluctuations to describe cosmology using the D4-D5-E6-E7-E8 model.
However, even if only a very small fraction of the spacetime geometries in the superposition contain closed timelike loops resulting from tilted lightcones, non-computable operations could be performed by a human-brain quantum computer.
The mass factor for gravitation has a visualization (arising from e-mail discussion with Dick Andersen). Gauge bosons are visualized as going from a source through a medium to a target. The graviton by itself is long-range and massless, but virtual Planck-mass black holes in spacetime absorb some of the gravitons as they go through the spacetime medium, thus weakening the gravitational force and producing the weaker effective gravitational force that is observed by experiments;
According to week 120 of This Week's Finds in Mathematical Physics by John Baez: , the Regge Calculus formalism of Gravitational Curvature was "... invented by Regge in 1961. Regge came up with a discrete analog of the usual formula for the action in classical general relativity. His formula applies to a triangulated 4-manifold whose edges have specified lengths. In this situation, each triangle has an "angle deficit" associated to it. It's easier to visualize this two dimensions down, ...[as in this figure
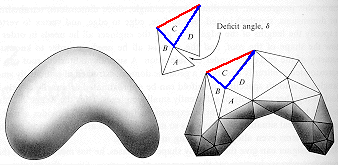
adapted from the book Gravitation, by Misner, Thorne, and Wheeler (Freeman 1972)]... where each vertex in a triangulated 2-manifold has an angle deficit given by adding up angles for all the triangles having it as a corner, and then subtracting 2 pi. No angle deficit means no curvature: the triangles sit flat in a plane.
The idea works similarly in 4 dimensions. Here's Regge's formula for the action: take each triangle in your triangulated 4-manifold, take its area, multiply it by its angle deficit, and then sum over all the triangles. Simple, huh? In the continuum limit, Regge's action approaches the integral of the Ricci scalar curvature - the usual action in general relativity. For more see ... T. Regge, General relativity without coordinates, Nuovo Cimento 19 (1961), 558-571. ...".
Note that the Regge Calculus of angle deficits only describes the Curvature part of Gravitation, and does not describe Torsion Gravitational effects. To see the Torsion part of Gravitation, the Regge Calculus must be given addtional structure, such as describing the edges of the 4-simplices by spinors in units of hbar instead of only by length magnitudes.
Since the Regge Calculus formulation of Gravitational Curvature
it has a correspondence with the MacDowell-Mansouri formulation of Gravitation
which is based on a local Spin(2,3) gauge Lie group (anti-deSitter) with 10 generators, having the characteristics of
Spin(2,3) comes from the Clifford algebra Cl(2,3) with graded structure 1+5+10+10+5+1.
The even subalgebra of Cl(2,3) is 1+10+5 = 16-dimensional, and is the Clifford algebra Cl(2,2) with graded structure 1+4+6+4+1 and dimensionality 16 = 2^4 = 1+4+6+4+1 = 4x4 = 4^2.The graded structure 1+4+6+4+1 of the even subalgebra of Cl(2,3) can be given a product so that it forms the 16-dimensional Lie algebra U(2,2) = U(1) x SU(2,2), with the 15-dimensional SU(2,2) corresponding to the 10+5 gradcd elements of Cl(2,3).
Note that in the D4-D5-E6-E7-E8 VoDou Physics model Gravitation is constructed, not just from anti-deSitter Spin(2,3) but from the larger Conformal Group Spin(2,4) of which Spin(2,3) is a subgroup.
Spin(2,4) comes from the Clifford algebra Cl(2,4) with graded structure 1+6+15+20+15+6+1.The 15-dimensional bivectors of Cl(2,4) can be given a product so that they form the 15-dimensional Conformal Lie algebra Spin(2,4) = SU(2,2), which corresponds to the 10+5 gradcd elements of Cl(2,3).
The Future Light Cone at a vertex of the 4-dim HyperDiamond lattice of D4-D5-E6-E7-E8 VoDou Physics is a 4-simplex
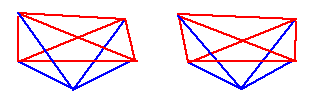
with the same graded structure 1+5+10+10+5+1 as the Cl(2,3) Clifford algebra:
When you add the Past Light Cone, you have two 4-simplices:
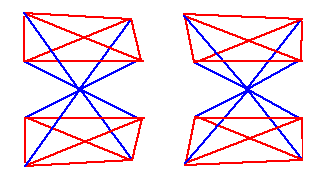
When you put in 12 further connections between Past and Future Light Cones, you have a total of six 4-simplices:
so that there are a total of six outer tetrahcdra.
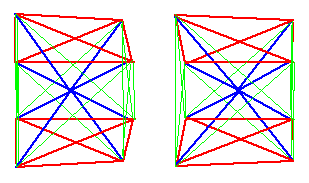
The 24 outer edges of the six outer tetrahedra correspond to the 24 vertices of a 24-cell:
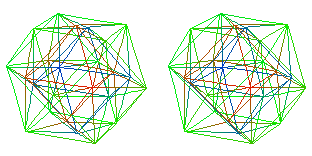
The 24-cell is the vertex figure of the D4 lattice. The D4 lattice is the even sublattice of the 4-dim HyperDiamond lattice of D4-D5-E6-E7-E8 VoDou Physics. That is, the D4 lattice can be described either as
...