As Onar Aam is a composer of music,
he has remarked that Western symphony instruments are linear, and are easily added together into a coherent whole that is a linear superposition of each part, and that many modern instruments (as rock guitar) and instruments from other cultures (as sitar) are non-linear, and have a greatly distorted sound that fills a large part of the spectrum, making them almost incompatible with other instruments. He then went on to say that a linear symphonic work (as a string quartet) could AS A WHOLE be distorted in a non-linear way (as by a bad stereo system) to produce A WONDERFUL HOWLING GUITAR INSTRUMENTAL PLAYED WITH CELLOS AND VIOLAS! THERE IS A BEAUTIFUL ANALOGY IN PHYSICS: Quantum field theories of electromagnetism, the weak force, and the color force can be expressed in terms of linear wavefunctions. The reason these quantum field theories work is that the linear wavefunctions have the property of superposition, that is, you can superpose a lot of them and you get another wavefunction that is a solution of the quantum field equations. All this takes place in a flat spacetime. So, quantum field theory of the first 3 forces is like a symphony orchestra. The 4th force, gravity, is VERY nonlinear - so much so, that it is hard to express it in terms of a quantum field theory, and gravity (in most formulations) stands alone because of its nonlinearity. Gravity is the nonlinear force. HOWEVER, if you FIRST use the superpositions of linear quantum fields of the first 3 forces to produce atoms, molecules, etc., and THEN apply gravity to the atoms, molecules, etc., you see that the atoms, molecules, etc., combine to form stars and planets and galaxies, AND the flat spacetime is curved by the gravity so that the stars, planets and galaxies move in orbits as we see them do. In a sense, OUR UNIVERSE IS A DISTORTED SYMPHONY!
Music has at least two important characteristics: Music evolves in time; and Music has mathematical structure.
According to our experience, the physical world evolves in time. The D4-D5-E6 model accounts for time evolution by using octonion structure. It identifies time with the real axis, so that it could do that with any of the real, complex, quaternion, or octonion numbers. Althogh it is necessary, a time axis is not sufficient for time evolution of the physical world. For physical time evolution, you need both a time axis and something (in the D4-D5-E6 model a spinor fermion such as a quark or electron) that experiences evolutionary change as it moves from its present point in spacetime to another point in its future lightcone. In the D4-D5-E6 model, the fundamental picture is that spacetime is a lattice of points that are connected by links. The spinor fermions are located at the points of the lattice. The evolutionary change comes when a spinor fermion moves from a point, along a future lightcone link, to another point. How can it evolve as it moves along the link? It must interact with something that lives on the link. In the D4-D5-E6 model, the things that live on the links of the lattice spacetime are gauge bosons, such as photons, gluons, gravitons, etc. For the interaction to produce an evolution that gives what I would call passage of time, it must be able to do three things to the spinor fermion: 1. carry energy from the spinor fermion to another spinor fermion at another point; 2. change the character of the spinor fermion (such from up electron to neutrino); and 3. carry energy from the spinor fermion to the spacetime lattice (so that a massive fermion can curve spacetime). In the D4-D5-E6 model, the way the gauge bosons interact (with the spinor fermions, and with each other) is determined by the Lie algebra of their gauge group. The real, complex, quaternion, and octonion numbers each determine a Lie algebra: The real numbers have no imaginary part, and so have only an empty or trivial Lie algebra. For them, there is only a time axis, but nothing to evolve on it. Real = trivial static stasis. The complex numbers have only a 1-dimensional imaginary part. Their Lie algebra is 1-dimensional U(1) = Spin(2). Since it is 1-dimensional, its basis is {i}, and the Lie algebra product is [i,i] = ii - ii = 0. In the D4-D5-E6 physics model, such gauge bosons are photons, and they can carry energy (dissipate it) but they cannot change a fermion or curve spacetime. Complex = dissipative. The quaternions have a 3-dimensional imaginary part. Their Lie algebra is 3-dimensional SU(2) = Spin(3). Since it is 3-dimensional, its basis is {i,j,k}, and the Lie algebra product is [i,j] = ij - ji = 2k , etc. Here, the Lie algebra product does not vanish, but takes the set {i,j,k} into itself. In the D4-D5-E6 physics model, such gauge bosons can be weak bosons, but they could only be a subset of the gluons or of the gravitons. As weak bosons, they can carry energy, and they can change electrons to neutrinos, but they cannot curve spacetime. Quaternions = dynamic stasis. The octonions have a 7-dimensional imaginary part. They do not form a Lie algebra, but expand into the 28-dimensional Lie algebra Spin(8) = S7xS7xG2. Here, the Lie algebra product no only does not vanish, but expands from 7 to 7+7+14=28 dimensions. In the D4-D5-E6 physics model, the 28 gauge bosons are: photon (1), weak bosons (3), gluons (8), and gravitons (15) plus a complex quantum phase (1). With octonions there are enough gauge bosons to carry energy, change fermions, and curve spacetime (plus have a quantum phase for interference experiments, which is a complex number in the D4-D5-E6 model). Octonions = evolutionary passage of time.
Onar Aam is working on the mathematical structure of music. As he says (in an e-mail message 12 Aug 95), the structure may be related to octonions: ------------------------------------------------- The octave:
| | || | | | || || | | | | || | | | || || | | | |_||_| | |_||_||_| | | | | | | | | | |__|__|__|__|__|__|__| i j k E I J K
Octonion reflexion has given me a new dearly needed tool to crack the code of musical harmony using octonions. Intuition has told me that there is a connection but I've only had three real clues to back it up. 1) 7 notes, 7 imaginaries 2) Tonika-Sub dominant-Dominant, quaternion triple 3) the octave *repeats* itself. It is fundamentally cyclic. How to preceed from here was somewhat of a puzzle for me because the seven keys do not add up trivially into the octonionic rules. Another problem was the fact that the octave is just a subset of the 12-tone scale. That the octave is a subset of the 12-tone scale I interpret as the octonion being embedded in a larger geometrical structure. This structure is related to the 24-cell. I stress that the octonion is still the arena of harmony. The 12-structure is just the background fundament from which the harmonic brilliance of the octonion stands out. Octonion harmony is nevertheless reflected in this structure. We recall that the octonion has a 3 + 4 or a 3 + 1 + 3 structure. Having in mind that the octonion is reflexive we should expect this structure to pop up quite a lot. The first appearence of this structure is immediately seen by observing the white keys on the keyboard. Each white key is separated by a black key except at two points in the octave in which the white keys intersect. This divides the octave into a 3 + 4 structure.
| | || | | | | || || | | | | || | | | | || || | | | |_||_| | + | |_||_||_| | | | | | | | | | | |__|__|__| |__|__|__|__| i j k E I J K
But from the imaginaries we see
that an 3 + 1 + 3 structure is also implicit,
namely where the IJK mirrors ijk and E is an Extraordinary number.
Is this also true?
Yes.
The keys corresponding to i,E and I are considered base harmonics.
I is called the Dominant because it "dominates" over E.
The reason is that harmonically IJK resembles ijk.
Just look at the keyboard.
The IJK section looks (and sounds) like a copy of the ijk section.
Finally we see a 3 + 1 + 3 structure if we play triad chords succesively
throughout the octave (i-k-I, j-E-J, k-I-K, E-J-i, I-K-j, J-i-k, K-j-E)
These make up 3 Major chords, 3 minor chords and 1 diminished.
Now over to the 12-structure.
We know that there are 7 white keys and 5 "background" black keys.
We may call it a 7+5 structure.
The tone which harmonizes best with i is i one octave up
(i.e. 12 halftones away).
The tone which harmonizes next best is the Dominant, I.
Guess how many halftones this is away from i.
That's right, 7.
So the chord i+I+i2 makes a 7+5 structure.
A very common pattern in music is INVERSION.
Inverting the 7+5 structure we get 5+7.
The chord which fits this pattern is i+E+i2,
and E as we recall is the Sub-dominant.
But let is stick with the 7-chord,
i.e. i+I.
Suppose these seven half tones are a mirror image
of the seven imaginaries.
We should then expect there to be a 3+4 structure in it.
Is there?
Yes!
The 4+3 = the Major chord (i+k+E), the most harmonic triad in music.
What about its inversion 3+4?
That makes up the Minor chord,
the second most harmonic triad in music.
This discourse contains no evidence, only indications.
Firm evidence requires a thorough understanding of
the 12-structure which the octonion is embedded in.
If this structure can be understood then
I think we will have a theory of music.
Onar.
-------------------------------------------------
TO EMBED
the 7-structure and the 5-structure in an octonionic 12-structure,
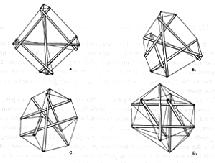
consider the Witting polytope in 8 real dimensions.
The Witting polytope also lives in 4 complex dimensions.
The Witting polytope can be constructed from the
4-dim 24-cell by a Golden Ratio expansion
of the 24-cell to a 24+96 = 120 vertex 4-dim polytope, the 600-cell.
It has octonionic structure and lives in 8-dim space.
Since the Witting polytope has 240 = 20x12 vertices,
it has 12-structure.
To see the 7 and 5 structures,
start with the 240-vertex Witting polytope in 8-dim,
and consider two of its projections in 4-dim,
the 600-cell and the 24-cell:
-------------------------------------------------
FIRST USE THE 600-CELL TO SEE THE 5-STRUCTURE:
The 600-cell has 120 vertices.
Each cell, or 3-dim face, is a tetrahedron.
A 3-dim projection of the 600-cell is an icosahedron,
with 12 vertices and 20 faces.
The faces are triangles, 5 at each vertex.
You could also look at the dual figure to the 600-cell,
the 120-cell with 600 vertices.
Each of the 120 cells are dodecahedra,
which have 20 vertices and 12 pentagon faces.
Consider the tetrahedron,
the cell (3-dim face) of the 600-cell.
It has 4 triangle faces, and 6 edges.
Note that an edge can be seen as a 2-sided polygon,
just as a triangle is a 3-sided polygon,
so you could say that a tetrahedron has 10 = 4 + 6 "faces".
Also, you can pair up the 4 faces and the 6 edges
(although it is a complicated thing to do with a
tetrahedron because of the lack of central symmetry)
to get from 10 "faces" = 4 triangles + 6 (2-sides) to
5 "faces" = 2 triangles + 3 (2-sides)
This structure is related to the tensegrity transformation
from the tetrahedron to the icosahedron:

------------------------------------------------- NOW USE THE 24-CELL TO SEE THE 7-STRUCTURE: The 12-structure of the 4-dimensional polytope,
the 24-cell, can be most clearly understood by noticing two things:
it has 24 vertices and 24 octahedra as 3-dim faces;
and
it can be projected into 3-dim space such that its
central figure is a 14-vertex polytope, the rhombic dodecahedron.
The way to picture the rohombic dodecahedron inside the 24-cell is
to consider the rhombic dodecahedron as containing an interior cube,
with the rhombic dodecahedron being built by adding a 4-sided pyramid
to each of the 6 faces of the interior cube.
Each of the 12 rhombic faces is a collapsed octahedron of the 24-cell,
with the rhombus being a cross-section of the octahedron.
That is,
the 2 outer vertices of the rhombic face are the
top and bottom vertices of the octahedron,
the 2 middle (on the interior cube) vertices are each
front and back side vertices of the octahedron, plus the edge between them,
and the 4 edges of the rhombic face are each
a side triangular face of the octahedron, plus edges.
Further, the rhombic face can be cut into 2 triangles, each of which
is 2 (front and back) triangular faces of the octahedron, plus edges.
That gives the 2 + 2x2 = 6 vertices,
the 2 + 4x2 + 2 = 12 edges, and
the 4 + 2x2 = 8 triangular faces
of the octahedron.
That accounts for 12 of the octahedra of the 24-cell.
Inside the rhombic dodecahedron there are 6 octahedra,
each with one vertex at the center of the rhombic dodecahedron
and one opposite vertex at one of the 6 outer vertices
of the rhombic dodecahedron.
The central square of each of those 6 octahedra is
a square face of the interior cube of the rhombic dodecahedron.
Each of those 6 octahedra is the projection of 2 octahedra of the 24-cell.
This accounts for all 12 + 2x6 = 24 octahedra of the 24-cell.
Since the rhombic docecahedron has 14 vertices,
and they are opposite each other,
you can get 7 vertices.
You can also consider the dual figure to the rhombic dodecahedron,
the cuboctahedron, which has 14 faces (8 triangles and 6 squares).
Since they are opposite to each other,
you can get 7 faces = 4 triangles + 3 squares.
-----------------------------------------------
THEREFORE the 7 and 5 structures in music
correspond to different projections of the Witting polytope
from 8 real dimensions into lower dimensions.
In some sense, the 7-structures are related to the 24-cell
and therefore to the ordinary 4-dim subspace
while
the 5-structures are related to the 600-cell
and therefore to the Golden sqrt(5) 4-dim subspace
of the 8-dim Witting polytope.
From the 4(complex)-dim point of view,
the 7-structures are REAL
and
the 5-structures are IMAGINARY.
Onar Aam's musical discussions also
deal with harmonic structures.
He associates the three division algebras (C ,Q and O) with
the Dissipative, the Autopoietic and the Reflexive.
Use the following correspondences:
C Q O
sine tone chord
C corresponds to the sine wave and
Q corresponds to harmonic combinations of sine waves.
The Sine wave is the most basic kind of tone.
When we combine sines harmonically
we do not experience them as many sines
but as _one_ tone, i.e. as a unity.
Instead of hearing individual sines
we experience them as _timbre_,
a kind of aural "color" gestalt.
Here is why:
When we play two sines with frequencies f1 and f2
simultaneously something strange happens perceptually.
In addition to the two sines we can also hear
a third imaginary tone f3 below with the frequency f2 - f1 .
Now, if we focus on this imaginary tone
instead of the two others then something odd happens.
The two real frequencies f1 and f2 vanish and instead
we experience them as the _timbre_ (or sharpness)
of the imaginary tone f3 .
In the quaternion product there is exactly such an annihilation.
If we multiply i and j then both i and j are annihilated and
a new imaginary k is simultaniously created.
The perceptual structure of combined sines is exactly
that of the quaternion multiplication.
The Ear works as a kind of differentiator.
If two sines with frequencies f1 and f2 are played together
then the ear will tend to hear a third frequency which
is the _difference_ between the two, f2 - f1.
When this process is applied to a harmonic sound
something rather strange happens.
A harmonic sound with basic frequency f
contains harmonics with frequencies 2f, 3f, 4f etc.
Now if we take the differences between all these frequencies
then we get the following:
4f-3f = 3f-2f = 2f-f = f
4f-2f = 3f-f = 2f
4f-f = 3f
As you see the delta-values maps into the original function.
If we continue to iterate this process
then all the values of the overtones will be mapped into f.
As a result we will only hear one frequency
in any harmonic sound, namely f.
All the other frequencies have self-annihilated
and mapped into f.
This of course does not mean that
the other frequencies have "disappeared".
Instead we now hear them as Timbre,
i.e. the sharpness and brightness of the sound.
This act of "disappearence" is what in phenomenology
is called _transparency_.
That is, the original sensations become invisible and
we see something else instead.
This is exactly how mirrors work too.
A mirror is just a surface that reflects light.
When we look into a mirror we don't see this surface,
but rather an object on the "other side".
Onar Aam has noted that
it is IMPOSSIBLE to create a STATIC 4-dimensional image of music.
The reason is as that music is essentially
a chain of _partial_ gestalts in time,
like a flow of information
rather than a single piece.
To visualize the D4-D5-E6-E7-E8 VoDou Physics model,
I have had to FIX (make static) part of the model (spacetime lattice)
to be able to comprehend enough to do calculations.
Fundamentally, the physics model is REALLY in flux,
and the spacetime lattice is not fixed and NOT STATIC.
Fundamentally, the physics model is LIKE MUSIC.
Also like music is genetic information.
It can even be represented by DNA sequence music (215k wav).
It may take a mind like Mozart's
to comprehend a complete piece of music,
or model of physics, or a DNA/RNA organism,
as a whole at once.
Dave Rusin has a web page about
In it, he says: "... unless you play nothing but octaves, say, you have two frequencies which are multiples of the first but not of each other. The most audible will be the lowest two, which are in a 3:2 ratio. This is the pure fifth, ... If we build fifths above the fifths, we get more tones in the scale (typically we reduce by an octave, i.e., a factor of 2, whenever producing a tone of more than twice the original frequency). This of course is the construction of the circle of fifths. ... the process never terminates: no power of (3/2) is ever a whole number of octaves (or indeed any integer multiple of the first frequency) ... So we fudge the fifth to make the equal-tempered scale: find a ratio r roughly equal to 3/2 so that some small power of r is a power of 2. This amounts to finding good integer approximations for the solutions of (3/2)^x = 2^y, which we rewrite as 3^k=2^l, or l/k=log3/log2=1.584962501... The theory of continued fractions tells us how to do this: Form the continued fraction expansion of this real number, stop at certain points, and reevaluate the fraction l/k which will approximate log3/log2. ... So here it is: log3/log2= cont.frac[1,1,1,2,2,3,1,5,2,23,...], which gives the following optimal approximations: 1/1, 2/1, 3/2, 8/5, 19/12, 65/41, 84/53. 485/306, 1054/667,... (I stop here because the next term to use, 23, is really large, so that 1054/667 is a much better appproximation than the 667 leads you to expect; the next best approximation has a huge denominator). ... I find it a curious twist of nature that the highly-divisible number 12 shows up here; ... Also I think it is interesting that the 12 shows up corresponding to the [1,1,1,2,2] part of the fraction; the next number (3) is larger so 19/12 is a pretty good approximant to log3/log2, considering the size of its terms; the 65/41, by contrast, is less impressively good. I guess nature just provided for us well. I think this explains the prevalence of the 5-note and 12-note scales." Note that the last integer 1 in the quoted early part of the continued fraction sequence corresponds to 84/53, indicating that a 53-note equal-tempered scale may have advantages over 41-note (coefficient 3) or 306-note (coefficient 5), and that a 53-note equal-tempered scale was discovered around 40 B.C. by King Fang, in China. It is interesting that the 53-note equal-tempered scale has the lowest number of notes with coefficient 1, and more notes than 2, since the 5-note and 12-note equal-tempered scales both have coefficent 2.
A Skytopia web page says: "... the standard (Chromatic) scale is made up of 12 notes or tones ...
Perhaps this has something to do with our brain's psychoacoustical response, with a bit of maths thrown in for good measure - but it's not really exactly clear why there are twelve notes. ...
... successive powers of 3 will 'complete' the scale after 12 iterations (the basis behind Pythagorean tuning), but this can't be the full story, since the twelth iteration (3^12 or 3^-12) is a fraction over (or under) the octave. This is infamously known as the so-called 'wolf' note. ...
... you can surround a single sphere perfectly with 12 identically sized spheres - with each sphere perfectly touching its neighbouring spheres (this forms the points of the cuboctahedron). Twelve also has the exclusive property of being the Gravitational Symmetry Limit - another sphere arrangement based on the icosahedron ...
... a little bit about each temperament. ...
... The 12-eT Vs. JI survey. Decide for yourself what tuning you prefer. ... Also see people's individual comments! ...".
Michael Rubinstein says, in his web page entitled The conspiracy of equal temperament:
"... Bach did not compose the Well Tempered Clavier to promote the equal tempered tuning system. Equal temperament actually did not come into use until the *20th* century. Bach's motivation for composing the WTC was to demonstrate the feasability of composing in well temperament and to demostrate the varying key colors in well tempered tuning as one progresses around the circle of fifths.The various well temperaments used in Bach's time are distinct from our equal temperament. (well temperament represented a departure from the various meantone tunings that were used in earlier music). ...
Equal temperament is appropriate for some music of the 20th century, especially atonal music, and music based on the whole tone scale, but not for the works of the 18th and 19th centuries. ...
The well temperaments used throughout the 17 and 18 hundreds also allow one to modulate amongst different keys. However, the octave is not divided into equal steps. Rather, some semi tones are smaller and some are larger. Overall, major fifths tend to be pretty close, while the quality of major thirds varies around the circle of fifths, with the more unstable major thirds tending to fall on the black keys, giving the various keys different characteristics. Composers of the 17 and 18 hundreds used this in their music. When we listen to their music in our modern equal temperament, we are not hearing their harmonic intentions. Key color has been lost. ...
If you don't believe me, you can read more about it in Owen Jorgensen's 1991 encyclopedic work: 'Tuning. Containing The Perfection of Eighteenth Century Temperament, The Lost Art of Nineteenth Century Temperament, and The Science of Equal Temperament'. He provides ample historical and scientific evidence for these ideas. The library call number for this masterpiece is MT 165 J667
What should you do if you want to play the music of Bach, Mozart, Beethoven, Chopin, etc the way it was intended? Find a competent piano tuner who knows how to tune historic well temperaments! ... In Austin, I recommend Charles Ball ... will have my piano tuned to Thomas Young's 1799 well temperament. Owen Jorgesen regards it as an idealization of the various well temperaments used. ...
I finally had my piano was finally retuned ala Thomas Young. My simple piano is bursting with character. I've never had more fun playing through my favorite pieces. The new tuning is also a source of improvisational inspiration, with the character of the keys suggesting various musical possibilities. Note for note, there is not much difference between Thomas Young's temperament and equal temperament (at most 9% of a semitone). However, the effect of playing various note combinations is substantial. ... in Thomas Young's temperament, because there are several perfectly tuned 5ths and 4ths, and depending on which key, some other very close intervals, the piano resonates like a gorgeous chime when the sustain pedal is pressed (thus freeing the other strings to resonate in sympathy with whatever sounds are present). One can spend hours just playing simple note combinations in Thomas Young and not get bored. ...".
Edward Dunne has a nice web page about equal temperament and continued fractions, in which he says: "... around 40 B.C., King Fang, in China, discovered the [84/53 approximation] ... In particular, Fang noticed that fifty-three perfect fifths are very nearly equal to thirty-one octaves. This leads to what is sometimes called the Cycle of 53. It can be represented by a spiral of fifths, replacing the more usual circle of fifths...."
N. J. A. Sloane writes and maintains The On-Line Encyclopedia of Integer Sequences. The continued fraction expansion for log_2(3) is in the Data Base of Integer Sequences Part 3: I A028507 S A028507 1,1,1,2,2,3,1,5,2,23,2,2,1,1,55,1,4,3,1,1,15,1,9,2,5,7, T A028507 1,1,4,8,1,11,1,20,2,1,10,1,4,1,1,1,1,1,37,4,55,1,1,49, U A028507 1,1,1,4,1,3,2,3,3,1,5,16,2,3,1,1,1,1,1,5,2,1,2,8,7,1,1 N A028507 Continued fraction expansion for log_2(3). R A028507 O A028507 1,4 K A028507 nonn,cofr H A028507 More info. H A028507 More info. A A028507 Tony Smith (tsmith@innerx.net) p A028507 Digits:=200: convert(evalf( log(3)/log(2) ),confrac);
According to Prof. Dr. Helmut Moritz (Physical Geodesy, Graz Technical University Austria) (in e-mail correspondence): "... Paul Hindemith ... in contrast to most other compose[r]s, was not a pianist but a professional viola player who led his own string quartet. So he had a very refined musical ear which was offended by the tiny impurities of the tempered scale and, in his book "Unterweisung im Tonsatz" ("A course of musical composition") he tried to replace it by intervals of rational numbers. This was not generally recognized, also because the musical fashion in those years (after 1930) was 12-tone music which made a dogma of the rigorous equality of all 12 tones of the chromatic scale. Fortunat[el]y, this dogma was later relaxed and now composers freely use all harmonic tools developed since Johann Sebastian Bach. The piano is now the standard instrument and would be unthinkable without the tempered scale, allowing free "enharmonic" modulation through all tonalities. Tonalities like A flat major of F minor, preferred by romantic composers such as Schubert, Schumann, Chopin and Liszt, would sound horribly on a diatonic piano before the introduction of the tempered scale. Schumann was an excellent pianist and accepted the situation but called the piano "the most unmusical instrument"... Most other people, including myself, do not hear the difference, and I fully accept the tempered scale for practical reasons. Curiously enough, new organs are now frequently built after some historical model, say in the pre-Bach Italian diatonic style. I once tried to play, on such an organ, a work of the late romantic composer Max Reger, and it sounded so badly that even I noticed the impurity. Last year I performed some analysis in Mathematica of Hindemith's proposal and approximation by continued fractions, referred to the tempered scale, and it turned out that Hindemith was acceptable, but the continued fractions were not. The best, for me, is still the tempered scale...".
In his mathematica notebook on Hindemith and his work "Unterweisung im Tonsatz", Helmut Moritz says:
"... The music of Pythagoras (around 500 B.C.) was primarily a theoretical and abstract subject. By means of his monochord (one string only) he studied simple integer ratios: octaves, fifth and fourths. Only these intervals were considered consonant ("poor but pure"). Thirds generated by superimposing 3 fifths (and subtracting 2 octaves), were considered "dissonant". (So the triad c - e - g was dissonant.). But he knew well the overtones; calling the following particularly bad third "Pythagorean" seems to me unfair. (Practically, the Greeks had a much richer musical material, even some kind of chromatic scale, and what is called "church scales": doric, lydic, ionic, etc, but harmony seems to have been poorly developed and little is known). Anyway, Pythagoras laid the foundation of both relativity and quantum theory: a^2 + b^2 = c^2 was the humble origin of line element ds^2 = dx^2 + dy^2 + dz^2 - dt^2 for Minkowski spacetime, and overtones were to become the corner stone of explaining quantum theory: the Fourier - Hilbert - Heisenberg vector and matrix mechanics, etc).... [ Helmut Moritz said in e-mail: "... Quantum Theory was founded independently in two completely different mathematicalforms by two equally great physicists, Heisenberg and Schroedinger. The miracle was that both mathematical formulations were soon recognized to be equivalent: the underlying Hilbert space may be formulated in two equivalent ways: as a space of functions or a space if infinite-dimensional vectors. A periodic function is equivalent to the infinite vector formed by its Fourier coefficients. ]...
- ... Diatonic Scales (up to and including JSBach's earlier "Inventions and Symphonies" for Piano): old church organs; playable keys: C major, c minor, D, d, E flat major, E , e, F, f, G, g, B flat major, b minor (13 keys out of 24)
- Tempered Scale (from later JSBach's "Das wohltemperierte Klavier"): all 24 keys playable, all "enharmonic modulations" possible; Haydn, Mozart, Beethoven, Schubert, Schumann, Liszt, Wagner, Richard Strauss, Debussy, Bartok, Gershwin, Schoenberg,...); all modern pianos, organs...
- .... Paul Hindemith - Hindemith' s chromatic scale systematically based on overtones; table from book "Unterweisung im Tonsatz", "A course of musical composition". He find as simple fractions as possible, guided by "systematic intuition" ...
... General Problem: To approximate the irrational numbers of the chromatic scale as closely as possibe by fractions that are as simple as possible There are several different general methods:
- 1. Pythagorean method: Piling up (or down) one fifth after the other (Slightly unfair terminology) THEORETICAL, limited power, but historically important and also practically used (in combination with Method 2) for tuning string instruments. ( By the way, Pythagoras was well aware of the overtones!)
- 2. Overtone method: PHYSICAL, refined, used by Hindemith
- 3. The MATHEMATICIAN immediately thinks of Continued Fractions - Reference: Edward. G. Dunne, "Pianos and Continued Fractions", INTERNET - In general, however, it is IMPOSSIBLE to obtain the Hindemith scale by a continued-fraction development of the tempered scale, as I had hoped originally. ...
The Pythagorean Comma - Eric Weisstein' s Encyclopedia of Music, INTERNET - Piling up 12 fifths should give the same as piling up 7 octaves, hence the following result should be ONE. The deviation from 1 is called a COMMA
The continued fractions are basic, however, for solving a DIFFERENT PROBLEM: Let us try to approximate optimally n octaves by m fifths. best approximation by as small m and n as possible
This is why our scale, in the Pythagorean or in the tempered or in the Hindemith variety, comes so NATURAL. Physically, of course, all goes back to the natural overtone scale. This is why we divide the octave into 12 (equal or slightly unequal ) parts rather than, for instance, into 22 parts. My guess is that this is based on the OVERTONE STRUCTURE OF OUR EAR. ...".
Here are some excerpts from some CD liner notes by Constantin Floros:
"... Johannes Brahms numbered ...[ Beethoven's last quartets ]... among the most imaginative of Beethoven's works, and Richard Wagner described the Quartet in C sharp minor [ Op. 131 ] as a "revelation from another world." ...... Gustav Mahler advocated that the quartets should be played orchestrally, as he was of the opinion that "performance by four players is wholly inadequate" ...
... with passage of time the enormous technical difficulties with which Ignaz Schuppanzigh and his colleagues had to struggle were overcome, so that Theodor Helm could write in 1910: "It is precisely those works of Beethoven which the great majority of his contemporaries described as confused, insufferable, even "crazy" (this epithet was applied to the last quartets almost universally for more than a lifetime) which now grip, thrill, involve and move us the most." It is curious that Beethoven himself foresaw this development. When the news was brought to him that one of his quartets, played by Schuppanzigh, had met with a poor reception, he said laconically: "One day it will please them." ...
... As to the Grosse Fugue, a critic described its first performance by the Schuppanzigh Quartet on 21 March 1826 "... as incomprehensible, "Chinese" ... the Babylonian confusion is complete; the result is a concert which only Moroccans can enjoy." ... the Viennese art and music dealer Matthias Artaria, who had already undertaken to publish the work, did everthing in his power to persuade Beethoven to replace the Fugue, "which is difficult to comprehend", by another finale [for the quartet Op. 130] "more accessible to the performers, and easier for the public to understand". He ... [declared] ... his willingness ... to publish the Grosse Fugue separately with an opus number of its own. Beethoven agreed to this proposal ... The question of what factors may have caused him to make so radical an alteration to his work is one which still engages the attention of scholars. ...".
When I listen to the dumbed-down substitute finale (movement 6 of the quartet Op. 130), it seems to me that Beethoven wrote it so boringly formulaic that it would be obvious to understanding listeners that they should replace it with the Grosse Fugue (which is what I do on CDs that I burn for my own listening). To make a physics analogy, I see the substitute movement 6 of Op. 130 as like conventional superstring theory (which in my opinion is, as physics, an idiotic mess although it does contain bits and pieces of interesting mathematics) and the Grosse Fugue as like the Clifford algebra structure that I like to use as a physics model foundation. The fugue structure looks to me like the periodicity of real Clifford algebras.
Beethoven's Op. 134, Grosse Fugue in B flat major, per piano a quattro mani, is the second of two compromises that Beethoven made with respect to the Grosse Fugue (the first being the final movement of Op. 130), but, unlike the first compromise, I think that the piano Grosse Fugue is interesting and illuminating, as it was made at the request of serious, intelligent pianists who wanted to be able to understand = play the Grosse Fugue.
Jean-Marc Bonard, in physics/0008053, has written
whose abstract states:
"An experimental study of strings, woodwinds (organ pipe, flute, clarinet, saxophone and recorder), and the voice was undertaken to illustrate the basic principles of sound production in music instruments. The setup used is simple and consists of common laboratory equipment. Although the canonical examples (standing wave on a string, in an open and closed pipe) are easily reproduced, they fail to explain the majority of the measurements. The reasons for these deviations are outlined and discussed.".
In the book Triangle of Thoughts (American Mathematical Society, 2001) Alain Connes, Andre Lichnerowicz, and Marcel Paul Schutzenberger discuss the interrelationships among Mathematics, Physics, and Philosophy. In Chapter 8, they say:
"... A.C. - ... I am trying to use a mathematical model that allows me to conceive of time in a way that is more fruitful and more individually satisfying than this dreadfully one-dimensional time upon which we inscribe our existence and which I find profoundly distasteful. ...
The first example that comes to mind ... is Kronecker's foliation, a straight line that winds at an irrational angle around a torus of very high dimension. ... most of the points of reference allowing us to feel and monitor time are cyclical rhythms ... There are a huge number of rhythms, each of which is a variable winding around in a circle. ... the multiple periods that, not being necessarily commensurate, allow us to imaging intuitive time as a high dimensional torus. There are as many dimensions as there are cyclical times ... Of course this can be compared to the linear physical time winding around this torus, if we trace the path of an individual. ...
M.P.S. - ... I wonder whether the simple problem of the coexistence of individual polycyclic time with its socialization is not virtually insoluble from the start.
A.C. - Not necessarily. These multiple cycles originate in a biological periodicity, which is common to a huge number of individuals. ... it is geographic proximity that imposes consistency and that causes the diverse parameters to be in phase within a particular society. Whenever the number of cyclical parameters is reduced, the "vital space" available to an individual is reduced. ... It has been observed that Anglo-Saxon societies are much more dependent on an affine time than are Mediterranean civilizations, which are much more familiar with polycyclic time. ... In Spanish literature, the individual's naive time is not one-dimensional, but rather a return time - return of the sun, of the moon - a time in which the accumulation associated with aging is not experienced in a drab bureaucratic manner.
... My assertion is that the one-dimensional model of time is too reductive for individual time. ... I am going to propose a model for you to examine. The universe in which you are located ... is that of language. ... I would say "the universe of words," simply to give it a name. ... I ... propose a ... definition of the "Self." ... It is simply the discrete information coded in the reproducible genetic information. The Universal Self is this immense genealogical tree that we are part of ... I consider myself to be a sort of translation, a material realization, of this abstract Self, through its interaction with physical reality. ...
M.P.S. - ... There is the consciousness of time, but there is also the consciousness of consciousness of time, which is not the same thing. ... I have reservations about the problem of language, because there are realities that are not verbal, such as music. ...
A.C. - All the same, music is transmissible and reproducible. It resembles a language. ... like a language it is written, spoken, and transmitted. ... I am fascinated by the relation between the usual model of time and the sequential nature of written language. This writing is perfectly adapted to associative algebra in the sense that the associativity condition simply means that a product of elements of an associative algebra can be written without the encumbrance of parentheses. ... Commutativity does not hold, but since sequential writing preserves the order of the terms of a product, it is perfect for handling non-commutativity. ...
a non-commutative algebra naturally engenders a one-parameter group of automorphisms that makes it evolve, that makes it rotate in such a way that the passage from xy to yx corresponds to what evolution yields for the purely imaginary value t = sqrt(-1) of the parameter t of the evolution group. We must ... introduce evolution only after choosing a state in the algebra, but the evolution obtained is modified only by inner automorphisms and these are in a certain sense invisible. Here, I believe, is the key link that Hamilton sought between time and algebra. ...
M.P.S. - Is musical notation sequential?
A.C. - I don't think so. Musical notation allows several themes to be developed simultaneously. Several melodies dan coexist and a dialogue can be established in the same instant; polyphony is a dialogue that is simultaneous, not sequential. In this sense, I think that music is an outline of a language that is inscribed in a multi-dimensional not sequential framework; it is a language that, except for certain musicians, cannot be effectively used as a means of communicating factual data ...
There are people who are capable of listening to an opera and hearing several voices at once. This is what made Victor Hugo jealous of Giuseppe Verdi.
M.P.S. - But you cannot compare the impressions that different people have when they listen to music.
A.C. - Not yet. ...
M.P.S. - ... Alain, you are sketching an image of evolving humanity: why do you believe it is evolving rather than static.?
A.C. - I can easily imagine the time when writing was never read silently, when it was transmissible only by reading aloud, so an oral reader was required. ... The time when one bought a book and read it silently came later. ...
Music in its current stage is analogous to oral reading: at this stage, the text can be transmitted only by the emission of sounds.
I claim there is another stage beyond this. I remember having heard the conductor Solti explain how he prepared for a concert. ... he simply took the score and holed up in a room where he would spend hours reading the score in silence.
M.P.S. - ... In other words, you conceive of the possibility of music that exists only in written form ...
A.C. - ... and that is inscribed in a time that would no longer be sequential, because a score is a multitude of chords, a tangle projected onto physical time of course, but that manifestly evolves in an higher dimensional space ...
M.P.S. - Silent reading must have begun in the 11th or 12th century, in Benedictine convents, so that the monks would not make too much noise reading. Little by little, people reached the stage of internalized reading. ... We know at what point people began to be taught to read directly by internalizing. It is a very curious phenomenon.
A.C. - Reading one voice is easy; reading a page of polyphony, as does a conductor, is much more difficult. ... music is still at the primitive stage, much more primitive than spoken language.
A.L. - Music is as old as language. ... social polycyclic time seems to me to be much more complicated.
A.C. - And it could be formalized by music.
M.P.S. - ... according to you, we can assume that the evolution of language can serve as a model for music. ... language begins with poetry rather than grammar; euphony plays a big role here.
A.C. - ... I sincerely believe that music is at its very beginnings, like language when it was at the stage of euphony. I think we migh succeed in this way to educate the human mind to deal with polyphonic situations in which several voices coexist, in which several states coexist ...
the problem of adaptation ... has to be resolved in order for us to understand quantum correlation and interrelation which we discussed earlier, and which are fundamentally schizoid in nature.
It is clear that logic will evolve in parallel with the development of quantum computers, just as it evolved with computer science. ...".
Tony Smith's Home Page ......