The 8-dimensional HyperDiamond lattice is made up of one hypercubic checkerboard D8 lattice plus another D8 shifted by a glue vector
Conway and Sloane, in their book Sphere Packings, Lattices, and Groups (3rd edition, Springer, 1999), in chapter 4, section 7.3, pages 119-120) define a packing
[ where the gule vector [1] = (1/2, ... , 1/2) ] and say: "... D+n is a lattice packing if and only if n is even.
D+n is what David Finkelstein and I named a HyperDiamond lattice (although in odd dimensions it is technically only a packing and not a lattice).
Conway and Sloane also say in chapter 4, section 7.1, page 117) that the lattice Dn is defined only for n greater than or equal to 3.
To see what happens for n = 2, note that D2 should correspond to the Lie algebra Spin(4),which is reducible to Spin(3)xSpin(3) = SU(2)xSU(2) = Sp(1)xSp(1) = S3xS3, and is not an irreducible Lie algebra. The root lattice of D2 is two copies of the root lattice of SU(2), which is just a lattice of points uniformly distributed on a line.
If you are to fit the two lines together, you have to specify the angle at which they intersect each other, and requiring "lattice structure" or consistency with complex number multiplication does NOT unambiguously determine that angle: it can be either
60 degrees, which gives you the A2 root lattice
*--* / \ * * \ / *--*
of the Lie algebra SU(3) and the Eisenstein complex integers
90 degrees, which gives you the C2 = B2 root lattice
*--*--* | | * * | | *--*--*
of the Lie algebra Spin(5) = Sp(2) and the Gaussian complex integers.
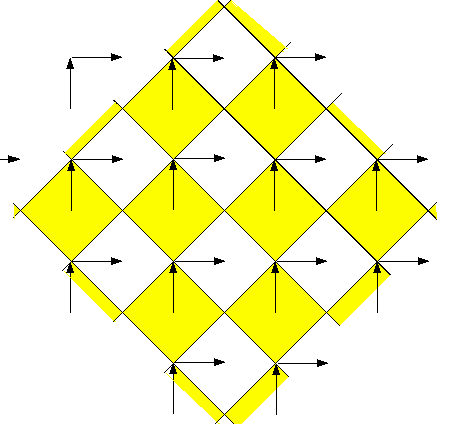
Since a Dn lattice for n > 3 is a checkerboard, or half of a hypercubic lattice, it is natural to define D2 as a checkerboard, or half of a C2 = B2 square lattice. Then the 2-dimensional HyperDiamond lattice D+2 = D2 u ( [1] + D2 ) is seen to be the Z2 square lattice C2 = B2

where the orginal D2 is made up of the centers of the yellow squares, the glue vectors are the (1/2,1/2) represented by pairs of arrows, and the ( [1] + D2 ) is made up of the centers of the white squares.
The total 2-dim hyperdiamond structure is the Z2 integer lattice, sort of analogous to the 4-dim case in which D4 u ( [1] + D4 ) = Z4, so that
Note that the basic D2 structure is consistent with Feynman's 2-dimensional checkerboard in which the lines of the checkerboard are 2-dim light-cone lines.
The E8 HyperDiamond lattice is used to construct the HyperDiamond Feynman Checkerboard model.
John Baez, in week 20 of This Weeks Finds, reviews the bookof Conway and Sloane, including icosians and E8
In the D4-D5-E6-E7-E8 VoDou Physics model, an 8-dimensional spacetime has the structure of an E8 lattice with Planck length lattice spacing.
If octonionic coordinate are chosen so that a given minimal vector in E8 is +1, the vectors in E8 that are perpendicular to +1 make up a spacelike E7 lattice.
The E8 8-dim spacetime lattice is made up of two D8 lattices.
(E8 is the D8+ lattice, sort of like the D3+ diamond non-lattice structure that is two D3 face-centered cubic lattices.)
The 8-dimensional E8 lattice has octonionic structure, but no nearest neighbor light-cone links.
To build the E8 Lattice: Begin with an 8-dimensional spacetime R8 = O, where a basis for O is {1,i,j,k,e,ie,je,ke} . The vertices of the E8 lattice are of the form
(a01 + a1e + a2i + a3j + a4ie + a5ke + a6k + a7je)/2 ,
where the ai may be either all even integers, all odd integers, or four of each (even and odd),
with residues mod 2 in the four-integer cases being (1;0,0,0,1,1,0,1) or (0;1,1,1,0,0,1,0) or the same with the last seven cyclically permuted.
E8 forms an integral domain of integral octonions.
The E8 lattice integral domain has 240 units:
±1, ±i, ±j, ±k, ±e, ±ie, ±je, ±ke, (±1±ie±je±ke)/2, (±e±i±j±k)/2, and the last two with cyclical permutations of {i,j,k,e,ie,je,ke} in the order (e, i, j, ie, ke, k, je).
The cyclical permutation (e, i, j, ie, ke, k, je) preserves the integral domain E8, but is not an automorphism of the octonions since it takes the associative triad {i,j,k} into the anti-associative triad {j,ie,je}.
The cyclical permutation (e, ie, je, i, k, ke, j) is an automorphism of the octonions but takes the E8 integral domain defined above into another of Bruck's cycle of seven integral domains. Denote the integral domain described above as 7E8, and the other six by iE8 , i = 1, ... , 6.
The 240 units of the 7E8 lattice corresponding to the integral domain 7E8 represent the 240 lattice points in the shell at unit distance (also commonly normalized as 2) from the origin (points on the line with iE8, jE8 notation are common points with the iE8 and jE8 lattices):
±1, ±i, ±j, ±k, ±e, ±ie, ±je, ±ke,
(±1 ±ie ±je ±ke)/2 (±e ±i ±j ±k)/2
(±1 ±ke ±e ±k)/2 5E8, 4E8 (±i ±j ±ie ±je)/2
(±1 ±k ±i ±je)/2 (±j ±ie ±ke ±e)/2
(±1 ±je ±j ±e)/2 6E8, 2E8 (±ie ±ke ±k ±i)/2
(±1 ±e ±ie ±i)/2 3E8, 1E8 (±ke ±k ±je ±j)/2
(±1 ±i ±ke ±j)/2 (±k ±je ±e ±ie)/2
(±1 ±j ±k ±ie)/2 (±je ±e ±i ±ke)/2
The other six integral domains iE8 are:
1E8: ±1, ±i, ±j, ±k, ±e, ±ie, ±je, ±ke,
(±1 ±je ±i ±j)/2 (±k±e±ie±ke)/2
(±1 ±j ±ie ±ke)/2 5E8, 6E8 (±i±k±e±je)/2
(±1 ±ke ±k ±i)/2 (±j±e±ie±je)/2
(±1 ±i ±e ±ie)/2 7E8, 3E8 (±j±k±je±ke)/2
(±1 ±ie ±je ±k)/2 2E8, 4E8 (±i±j±e±ke)/2
(±1 ±k ±j ±e)/2 (±i±ie±je±ke)/2
(±1 ±e ±ke ±je)/2 (±i±j±k±ie)/2
2E8: ±1, ±i, ±j, ±k, ±e, ±ie, ±je, ±ke,
(±1 ±i ±k ±e)/2 (±j,ie,je,ke)/2
(±1 ±e ±je ±j)/2 7E8, 6E8 (±i±k±ie±ke)/2
(±1 ±j ±ke ±k)/2 (±i±e±ie±je)/2
(±1 ±k ±ie ±je)/2 1E8, 4E8 (±i±j±e±ie)/2
(±1 ±je ±i ±ke)/2 3E8, 5E8 (±j±k±e±ie)/2
(±1 ±ke ±e ±ie)/2 (±i±j±k±je)/2
(±1 ±ie ±j ±i)/2 (±k±e±je±ke)/2
3E8: ±1, ±i, ±j, ±k, ±e, ±ie, ±je, ±ke,
(±1 ±k ±ke ±ie)/2 (±i±j±e±je)/2
(±1 ±ie ±i ±e)/2 7E8, 1E8 (±j±k±je±ke)/2
(±1 ±e ±j ±ke)/2 (±i±k±ie±je)/2
(±1 ±ke ±je ±i)/2 2E8, 5E8 (±j±k±e±ie)/2
(±1 ±i ±k ±j)/2 4E8, 6E8 (±e±ie±je±ke)/2
(±1 ±j ±ie ±je)/2 (±i±k±e±ke)/2
(±1 ±je ±e ±k)/2 (±i±j±ie±ke)/2
4E8: ±1, ±i, ±j, ±k, ±e, ±ie, ±je, ±ke,
(±1 ±ke ±j ±je)/2 (±i±k±e±ie)/2
(±1 ±je ±k ±ie)/2 1E8, 2E8 (±i±j±e±ke)/2
(±1 ±ie ±e ±j)/2 (±i±k±je±ke)/2
(±1 ±j ±i ±k)/2 3E8, 6E8 (±e±ie±je±ke)/2
(±1 ±k ±ke ±e)/2 7E8, 5E8 (±i±j±ie±je)/2
(±1 ±e ±je ±i)/2 (±j±k±ie±ke)/2
(±1 ±i ±ie ±ke)/2 (±j±k±e±je)/2
5E8: ±1, ±i, ±j, ±k, ±e, ±ie, ±je, ±ke,
(±1 ±j ±e ±i)/2 (±k±ie±je±ke)/2
(±1 ±i ±ke ±je)/2 2E8, 3E8 (±j±k±e±ie)/2
(±1 ±je ±ie ±e)/2 (±i±j±k±ke)/2
(±1 ±e ±k ±ke)/2 7E8, 4E8 (±i±j±ie±je)/2
(±1 ±ke ±j ±ie)/2 1E8, 6E8 (±i±k±e±je)/2
(±1 ±ie ±i ±k)/2 (±j±e±je±ke)/2
(±1 ±k je ±j)/2 (±i±e±ie±ke)/2
6E8: ±1, ±i, ±j, ±k, ±e, ±ie, ±je, ±ke,
(±1 ±e ±ie ±k)/2 (±i±j±je±ke)/2
(±1 ±k ±j ±i)/2 3E8, 4E8 (±e±ie±je±ke)/2
(±1 ±i ±je ±ie)/2 (±j±k±e±ke)/2
(±1 ±ie ±ke ±j)/2 5E8, 1E8 (±i±k±e±je)/2
(±1 ±j ±e ±je)/2 7E8, 2E8 (±i±k±ie±ke)/2
(±1 ±je ±k ±ke)/2 (±i±j±e±ie)/2
(±1 ±ke ±i ±e)/2 (±j±k±ie±je)/2
The vertices that appear in more than one lattice are:
±1, ±i, ±j, ±k, ±e, ±ie, ±je, ±ke
in all of them;
(±1±i±j±k)/2 and (±e±ie±je±ke)/2 in 3E8, 4E8, and 6E8 ;
(±1±i±e±ie)/2 and (±j±k±je±ke)/2 in 7E8, 1E8, and 3E8 ;
(±1±j±e±je)/2 and (±i±k±ie±ke)/2 in 7E8, 2E8, and 6E8 ;
(±1±k±e±ke)/2 and (±i±j±ie±je)/2 in 7E8, 4E8, and 5E8 ;
(±1±i±je±ke)/2 and (±j±k±e±ie)/2 in 2E8, 3E8, and 5E8 ;
(±1±j±ie±ke)/2 and (±i±k±e±je)/2 in 1E8, 5E8, and 6E8 ;
(±1±k±ie±je)/2 and (±i±j±e±ke)/2 in 1E8, 2E8, and 4E8 .
The unit vertices in the E8 lattices do not include any of the 256 E8 light cone vertices, of the form (±1±i±j±k±e±ie±je±ke)/2.
They appear in the next layer out from the origin, at radius sqrt 2, which layer contains in all 2160 vertices.
In the image below,
the 240 in the first layer look like  the
112 look like
the
112 look like 
the 256 look like  in the second the 1792 look like
in the second the 1792 look like  (7 copies of 128+128).
(7 copies of 128+128).
The real 4_21 Witting polytope of the E8 lattice in R8 has
6,720 edges;
60,480 triangular faces;
241,920 tetrahedra;
483,840 4-simplexes;
483,840 5-simplexes 4_00;
138,240 + 69,120 6-simplexes 4_10 and 4_01; and
17,280 7-simplexes 4_20 and 2,160 7-cross-polytopes 4_11.
The E8 lattice in R8 has a counterpart in C4, the self-reciprocal honeycomb of Witting polytopes, a lattice of all points whose 4 coordinates are Eisenstein integers with the equivalent congruences
u1 + u2 + u3 = u2 - u3 + u4 = 0 (mod i sqrt(3)) and
u3 - u2 = u1 - u3 = u2 - u1 = u4 (mod i sqrt(3)).
The self-reciprocal Witting polytope in C4 has
240 vertices,
2,160 edges,
2,160 faces, and
240 cells.
It has 27 edges at each vertex.
Its symmetry group has order 155,520 = 3 x 51,840.
It is 6-symmetric, so its central quotient group has order 25,920.
It has 40 diameters orthogonal to which are 40 hyperplanes of symmetry,each of which contains 72 vertices.
It has a van Oss polygon in C2, its section by a plane joining an edge to the center, that is the 3{4}3 in C2, with 24 vertices and 24 edges.
The 24-cell 3{4}3 in R4 has
24 vertices,
96 edges,
96 faces, and
24 cells.
The Witting honeycomb has a van Oss apeirogon that is a 3{4}6, whose vertices and edges are the vertices and faces of the real tessellation of triangles {3,6}.
The vertices of a 3{4}6 can be represented as the Eisenstein integers a + bw,
where w = (- 1 + i sqrt(3))/2 is a complex cube root of unity.
REFERENCES:
Conway and Sloane, Sphere Packings, Lattices and Groups, 2nd ed, Springer 1993.
Coxeter, Regular Polytopes, Dover 1973 (reprint from 1963).
Coxeter, Regular and Semi-Regular Polytopes. III. Math. Z. 200, 3-45, 1988.
Coxeter, Regular Complex Polytopes, 2nd ed, Cambridge 1991.
Edward Dunne has a nice WWW page about the Lie group E8.
......