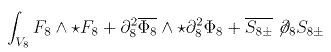Introduction to my May 2002 Cookeville Clifford Algebra talk:

 

Complex Clifford Periodicity

Cl(2N;C) = Cl(2;C) x ...(N times tensor product)... x Cl(2;C)

Cl(2;C) = M2(C) = 2x2 complex matrices

spinor representation = 1x2 complex column spinors

Hyperfinite II1 von Neumann Algebra factor is the completion of the union of all the tensor products

Cl(2;C) x ...(N times tensor product)... x Cl(2;C)

By looking at the spinor representation, you see that "the hyperfinite II1 factor is the smallest von Neumann algebra containing the creation and annihilation operators on a fermionic Fock space of countably infinite dimension."

In other words, Complex Clifford Periodicity leads to the complex hyperfinite II1 factor which represents Dirac's electron-positron fermionic Fock space.

Now, generalize this to get a representation of ALL the particles and fields of physics.

 

Use Real Clifford Periodicity to construct a Real Hyperfinite II1 factor as the completion of the union of all the tensor products

Cl(1,7;R) x ...(N times tensor product)... x Cl(1,7;R)

where the Real Clifford Periodicity is

Cl(N,7N;R) = Cl(1,7;R) x ...(N times tensor product)... x Cl(1,7;R)

The components of the Real Hyperfinite II1 factor are each

Cl(1,7;R)

[ my convention is (1,7) = (-+++++++) ]

Cl(1,7) is 2^8 = 16x16 = 256-dimensional, and has graded structure

1   8   28   56   70   56   28   8   1
What are the physical interpretations of its representations?

There are two mirror image half-spinors, each of the form of a real (1,7) column vector with octonionic structure.

The 1 represents:

The 7 represent:
One half-spinor represents first-geneneration fermion particles, and its mirror image represents first-generation fermion antiparticles.

Second and third generation fermions come from dimensional reduction of spacetime, so that

There is a (1,7)-dimensional vector representation that corresponds to an 8-dimensional high-energy spacetime with octonionic structure

that reduces at lower energies to quaternionic structures that are

There is a 28-dimensonal bivector representation that corresponds to the gauge symmetry Lie algebra Spin(1,7)

that reduces at lower energies to:

There is a 1-dimensional scalar representation for the Higgs mechanism.

The above structures fit together to form a Lagrangian

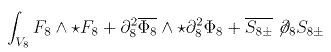
that reduces to a Lagrangian for Gravity plus the Standard Model.

Representations have geometric structure related to E6

E6 is an exceptional simple graded Lie algebra of the second kind:

E6 = g = g-2 + g-1 + g0 + g1 + g2

g0 = so(1,7) + R + iR

dim g-1 = 16

dim g-2 = 8

This gives real Shilov boundary geometry of S1xS7 for (1,7)-dimensional high-energy spacetime representation and for the first generation half-spinor fermion representations.

The geometry of the representation spaces, along with combinatorial structure of second and third generation fermions, allows calculation of relative force strengths and particle masses:

 

 

 

However:

Fermilab says that the T-quark mass is about 170 GeV.

?? Which is the True T-quark mass: 130 or 170 ??

 

 

 

 

 

The quote is from John Baez's web page week 175 at http://math.ucr.edu/home/baez/week175.html

E6 GLA structure is from Soji Kaneyuki's writing in Analysis and Geometry on Complex Homogeneous Domains, by Jacques Faraut, Soji Kaneyuki, Adam Koranyi, Qi-keng Lu, and Guy Roos (Birkhauser 2000).

Frank D. (Tony) Smith, Jr., Cartersville, GA, March 2002http://www.innerx.net/personal/tsmith/TShome.html