Tony's Home
A Classical
Radius Black Hole in
Ordinary SpaceTime is
connected through a Ring
Singularity to a Compton Radius
Vortex in Exotic SpaceTime.
A Compton
Radius Vortex in
Ordinary SpaceTime is
connected through a Ring
Singularity to a Classical Radius Black
Hole in Exotic SpaceTime.
At the Planck Mass, the Classical Radius equals the Compton
Radius, so that a Planck Mass Black Hole is also a Planck Mass
Compton Radius Vortex, so that
a Planck
Radius Vortex Black Hole
lives in both Ordinary
SpaceTime and Exotic
SpaceTime, acting as a Bridge or Window or Pivot between
Ordinary SpaceTime and
Exotic SpaceTime, so I call it
the
Planck Pivot Vortex
whose Symmetry Group
is
The Planck Pivot Vortex gives rise to Planck Fulcrum
Ordinary/Exotic Duality Equations for Length L and Mass M:
L(ordinary) L(exotic) = Lplanck^2
M(ordinary) M(exotic) = Mplanck^2
It took several e-mail messages from Jack
Sarfatti to convince me that we can go below the Planck
Scale.
One reason that I thought that we could not go below the Planck
Scale was what Feynman said in his book QED (Princeton Press
paperback 1988), from footnote 1 on page 129: "... perhaps the idea
that two points can be infinitely close together is wrong ... If
we make the minimum possible distance between two points as small as
10^(-100) centimeters (the smallest distance involved in any
experiment today is
around 10^(-16) centimeters), the infinities disappear, all right -
but other inconstencies arise, such as the total probability of an
event adds up to slightly more or less than 100%, or we get
negative energies in infinitesimal amounts. It has been suggested
that these inconsistencies arise because we haven't taken into
account the effects of gravity - which are normally very, very weak,
but become important at distances of [ the Planck Scale,
10^(-5) gm, or ] 10^(-33) cm."
What I had not realized was that, as Kip Thorne says in his book
Black Holes and Time Warps (Norton 1994, pages 491-492), "... in 1974
... Hawking inferred as a byproduct of his discovery of black hole
evaporation ... that vacuum fluctuations near a [Black
Hole]'s horizon are exotic: They have negative
average energy density as seen by outgoing light beams near the
hole's horizon. ... it is this exotic property of the vacuum
fluctuations that permits the hole's horizon to shrink as the hole
evaporates ... The horizon distorts the vacuum fluctuations away from
the shapes they would have on Earth, and by this distortion it makes
their average energy density negative,that is, that is, it makes the
fluctuations exotic. ... Gunar Klinkhammer ... has proved that in
flat spacetime ... vacuum fluctuations can never be exotic ... Robert
Wald and Ulvi Yurtsever have proved that in curved spacetime ... the
curvature distorts the vacuum fluctuations and thereby makes them
exotic. ...".
Feynman's Negative Energies below the Planck Scale are due
to Exotic SpaceTime Vacuum Fluctuations.
The Planck-Scale 4-dimensional
HyperDiamond Lattice used in the D4-D5-E6-E7
physics model is not fundamental because it is the latttice
at the smallest possible scale, it is fundamental because it
is the
There are 3 possible types of particles connecting
Ordinary SpaceTime and
Exotic SpaceTime.
Here are orders of magnitudes of examples of each type:
Electron, Planck Mass Black Hole,
Solar Mass Black Hole, and our
Universe
based on the Planck Fulcrum Ordinary/Exotic Duality Equations:
L(ordinary) L(exotic) = Lplanck^2
M(ordinary) M(exotic) = Mplanck^2
ORDINARY SPACETIME BOTH EXOTIC SPACETIME
Electron Ring
Compton Radius Vortex Singularity Classical Black Hole
10^(-11) cm 10^(-55) cm
10^(-27) gm 10^17 gm
Planck Mass Black Hole
Compton Radius Vortex = Classical Black Hole
10^(-33) cm = 10^(-33) cm
10^(-5) gm = 10^(-5) gm
Solar Mass Black Hole Ring
Classical Black Hole Singularity Compton Radius Vortex
10^5 cm 10^(-71) cm
10^33 gm 10^(-43) gm
Universe Ring
Classical Black Hole Singularity Compton Radius Vortex
10^28 cm 10^(-94) cm
In Each of the 3 types, the Structure is a Sarfatti
4-Mouth Structure:
- Compton/Classical Vortex/Black Hole
Mouth in Ordinary SpaceTime
- Ring Singularity Mouth in Ordinary
SpaceTime
- Ring Singularity Mouth in Exotic
SpaceTime
- Classical/Compton Blackole/Vortex in
Exotic SpaceTime
Each of the 3 types of 4-Mouth Structures has its own
Symmetry Group:
Compton Radius Vortex in Ordinary
SpaceTime: K4
Classical Black Hole in Ordinary
SpaceTime: Z3 \ Z2
Planck Pivot Vortex: (K4 \ Z3) \ Z2 =
TD
The interplay between Ordinary SpaceTime and Exotic SpaceTime is
important in
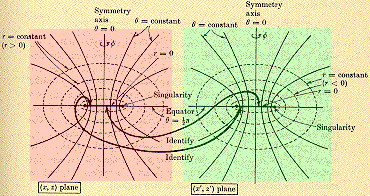
Start with a
with a^2 greater than m^2:
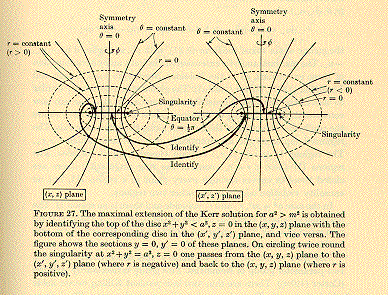
Roughly, this looks like
A 1
_____________ _____________
B 2
where
the lines ___________ are edge-on views of the ring
singularity,
the line between 1 and 2 is the ring singularity in the ordinary
part of the extended spacetime in which distances are positive and
gravity is attractive, and
the line between A and B is the same ring singularity in the
exotic part of the extended spacetime in which distances are negative
and gravity is repulsive.
Since the A and B sides of the exotic singularity differ from the
1 and 2 sides of the ordinary singularity in that distances are
negative or positive, respectively, and
since the A and 1 sides differ from the 1 and 2 sides in that they
are on the top and bottom of the singularity as defined by its spin
on its axis,
The External Symmetries of a Compton Radius Vortex are those
of Position in SpaceTime, Mass=Area, Spin=Angular Momentum, Electric
Charge, and Color
Charge.
The Internal Symmetry Group of the Compton Radius Vortex
Kerr-Newman Black Hole with a^2 greater than m^2 is the Klein 4-group
K4.
For particles such as leptons and quarks that are less massive
than the Planck Mass Mplanck, the Classical Radius given by G M^2 / R
is much smaller than the Compton Radius given by hbar / M c. Some
examples of Classical and Compton Radii are:
- Massless Neutrino - RclassicalNeutrino = 0 - RcomptonNeutrino
= scale of Universe
- Electron - RclassicalElectron = 10^(-55) cm - RcomptonElectron
= 10^(-11) cm
- Quark - RclassicalQuark = 10^(-52) cm - RcomptonQuark =
10^(-13) cm
- Planck Mass - RclassicalPlanck = 10^(-33) cm =
RcomptonPlanck
If you tried to probe the Electron or Proton within their Compton
Radius Vortex all the way down to its Classical Radius, you would
have to use a probe whose energy is on the order of hbar / Rclassical
c. For the Electron, it would be EprobeElectron = 10^41 GeV, and for
a Quark it would be EprobeQuark = 10^38 GeV, both far more energetic
than the Planck Energy Eplanck = 10^19 GeV.
Since any energy higher than Eplank = 10^19 GeV would disrupt
SpaceTime by graviton creation of new
SpaceTime forming a Black Hole of mass at least the Planck Mass
Mplanck = 10^19 GeV,
the Classical Radius Vortex of Electrons, Quarks, and
other particles less massive than the Planck Mass Mplanck = 10^19 GeV
does not exist in Ordinary SpaceTime,
but lives in Exotic SpaceTime.
The only elementary particles for which the
Classical Radius
is greater than the Compton Radius are Black
Holes with mass greater than the Planck Mass.
The Compton Radius Vortices of Black Holes larger than Planck
Mass do not exist in Ordinary
SpaceTime, but live in Exotic
SpaceTime.
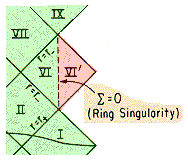
The Maximal Extension of SpaceTime for such a Black Hole is shown
in Figure 12.4 from General Relativity by Robert M. Wald (Chicago
1984):
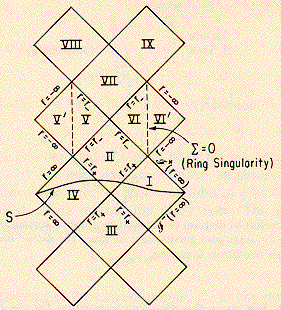
At such a Black Hole, you can travel from External SpaceTime
Region I to Extenal SpaceTime Region IX by going through 3 Regions,
Regions II, VI, and VII, that are inside Event Horizons.
Also, you can travel through the Ring Singularity such as from
Region VI to Region VI' and back to Region VI.
The External Symmetries of a Classical Radius Black Hole are those
of Position in SpaceTime, Mass=Area, Spin=Angular Momentum, Electric
Charge, and Color
Charge.
The Internal Symmetry Group of a Classical Radius Black
Hole is
an extension (denoted by \ ) of
the cyclic group Z3 of the 3 Interior
Regions
of the journey from Region I to Region IX and
the group Z2 of going through the Ring
Singularity
from Region VI to Region VI' and back
so that the total Symmetry Group is an extension \
Z3 \ Z2
Only for a Planck Mass Black Hole
(of mass 10^19 GeV and radius 10^(-33) cm, for which the
Classical Radius equals the Compton Radius)
can
both the Classical Radius and the Compton
Radius
be observed from both Ordinary
SpaceTime and Exotic SpaceTime,
forming a Bridge or Window or Pivot between them,
so that a Planck Mass Black Hole has Symmetry Group that is an
extension (denoted by \ ) of the extension Z3 \ Z2 of the Classical
Radius Black Hole and K4 of the Compton Radius Vortex
so that the ingredients K4, Z3, and Z2 produce T = A4 = K4 \ Z3
and TD = T \ Z2, and
(K4 \ Z3) \ Z2 = TD
is the 24-element Symmetry Group of a Planck Mass Black Hole.
TD, the Binary Tetrahedral Group, or
Double A4,
is the McKay group for E6 of the
D4-D5-E6-E7 physics model.
E7, whose McKay group is OD,
the 48-element Binary Octahedral Group, or Double S4D, appears in
the D4-D5-E6-E7 physics model as the
group of the Super Implicate Order
Macrospace.
The 24-element Octahedral Group O, which is double-covered by OD,
is the Symmetric Group S4.
Jack Sarfatti remarks
(with respect to his closely related structures that motivated me to
write this page): "... Note you get the full S4 symmetry at the
Planck mass. The symmetry is broken when you move off the Planck
scale. ... That's what we want. ...".
Saul-Paul Sirag remarks
(with respect to his closely related structures that motivated me to
write this page): "... Ezekiel saw the 4 cherubim. John's vision of
the throne of God in the book of Revelation has 4 "living creatures"
(zoon in Greek) around the throne, and 4! = 24 elders surrounding the
throne. Of course the main number, repeated over and over is 7, which
goes back to the 7 days of Creation + Sabboth. But there is a deep
connection between S4 and 7 as we will see. [Aside: For a while,
I called the 4 objects permuted by S4 Zons.] ... Carl Jung has
pointed out that the 4 cherubim correspond to 4 cardinal figures of
the Zodiac. (He was undoubtedly not the first to notice this.) From
Jung we may pass to Arthur Young, who was a student of Jungian
symbolism (he went through a long Jungian analysis, which he credited
with the cure of his paralyzed arms -- but that's another story. Jung
had emphasized the symbolism of fourness, in addition to the well
known threeness of the Christian trinity. Because of Arthur Young's
fascination with the fourness, he was very intrigued with the
tetrahedron. In March of 1974 he asked me (as his "research
associate" at the Institute for the Study of Consciousness, which he
set up in the fall of 1973) to work out the group table for the
symmetries of the tetrahedron. ... the rotations of the tetrahedron
have the symmetry group consisting of the 12 even permutations of 4
objects (this is called the alternating-4 group, A4, and also the
tetrahedral group, T. Moreover, the full symmetry group (which
includes reflections) is the set of all permutations of 4 objects,
the symmetric-4 goup, labeled S4, and also called the octahedral
group, O, because it is the rotational symmetry group of the
octahedron (and cube which is the dual figure). One of the things I
learned while working out this S4 group table was that I could take
short cuts by way of the structure of the Klein-4 group K4 as a
subgroup of S4. In standard group theory languange, S4 is the
semi-direct product of the K4 group and S3, the Symmeric-3 group.
Thus there are 6 cosets of K4 in S4. In other words, I stumbled onto
the concept of cosets without knowing what they were called. Sometime
in 1980, Abdas Salam sent Jack a copy of his Nobel Prize address
(1973). In it Salam mentions 24 particles (18 quarks in 3 families
and 3 colors; and 6 leptons in 3 families). Jack made the claim that
these 24 particles must correspond to the 24 elements of S4. I looked
at my S4 table and saw immediately that since there are 5 classes of
S4 elements, and that there were 1, 3, & 8 elements making up the
even permutations of the A4 subgroup, while the remaining 12 elements
separate into two classes each containtin 6 elements. It looked like
the even permutations would correspond to gauge bosons, and the odd
permutations would correspond to basic fermions. After all 1, 3, 8,
6, 6 had become a particle physics mantra: 1 photon, 3 weakons, 8
gluons, 6 quarks, 6 leptons. The multiplication of permutations would
match the basic rule of particle physics: fermions interact by
exchanging bosons; bosons can interact with each other, by exchanging
bosons. Moreover, the cosets of K4 arranged these 12 odd permutations
as 2 of each class in three separate cosets. The idea that group
multiplicaton of elements modeled particle interactions was, of
course, a radically new idea. This was the jumping off point for the
development of the S4 (Octahedral) group algebra theory of the
unification of the forces (other than gravity). The Standard Model
Lie groups are imbedded as a Principal fiber bundle (the unitary
elements) in the Group Algebra C[S4], also known as the
octahedral group algbra C[O] In order to bring in gravity, I
went to the double cover of O, the octahedral double group OD. The
group algebra C[OD] = C[O] + P + D, where P is the
complex Pauli algebra and D is the complex Dirac algebra (which are
complex Clifford algebras, i.e. complex C(3) and complex C(4). There
are now 8 classes in OD, which correspond to 8 basic representations,
and thus to 8 total matrix algebras of dimensions 1, 2, 3, 4, 3, 2,
1, 2. By the correspondence proved by John McKay (1979) these are
what I call "balance" numbers of the E7 Lie algebra. ... I have been
pushing the idea that the entire set of A-D-E
Coxeter graphs is implicated in the ultimate
description of reality. This is because the A-D-E graphs have
been shown by mathematicians in recent decades to be a ubiquitous
classification structure. At least 20 different mathematical objects
have been brought into this scheme -- Lie algebras
(and groups), Coxeter (Weyl) reflection
groups, finite subgroups of SU(2), which I call McKay
groups, catastrophe structures, singularities (of differentiable
maps), 2-d conformal field theories, graviational instantons,
error-correcting codes -- to name only a few
of the well known (and of great interest to physics). ... Each of the
A-D-E classifications is merely a different window into some vast
object (Vast Active Living Inteligent System -- a la Phillip K.
Dick?) What is clear through one window is seen only dimly (or not at
all) through another. The A-D-E Coxeter graphs provide a way to
transform from one type of object to another, or to transform within
a particular type. There is an infinite number of A's, and an
infinite number of D's beginning with D4, and only three E's: E6, E7,
E8. ... The D series begins with D4, so
we are back to 4 again. ..."
My remarks are that these symmetries are consistent with the
HyperDiamond Lattice structure of the
D4-D5-E6 physics model, and that
Saul-Paul's work with S4 was a key that led me to construct the
D4-D5-E6 physics model. Unlike Jack and
Saul-Paul, I use the 24-element
Double-cover Tetrahedral group TD (also called the Binary Tetrahedral
Group) instead of the 24-element Octahedral group O = S4, but
there is much similarity among the various approaches.
All these fascinating symmetries are related to mental
pictures that Jack Sarfatti, Saul-Paul Sirag, Nick Herbert, Dimi
Chakalov, and I have had, and to the images
and ideas of Mark Thornally:

How deeply have we probed within a Compton Radius
Vortex?
What have we seen?
If you tried to probe the Gaja/Ganesha
Electron or Proton inside its Compton Radius Vortex all the way down
to its Classical Radius, you would have to use a probe whose energy
is on the order of hbar / Rclassical c. For the Electron, it would be
EprobeElectron = 10^41 GeV, and for a Quark it would be EprobeQuark =
10^38 GeV, both far more energetic than the Planck Energy Eplanck =
10^19 GeV. Since any energy higher than Eplank = 10^19 GeV would
disrupt SpaceTime by graviton creation of new
SpaceTime forming a Black Hole of mass at least the Planck Mass
Mplanck = 10^19 GeV, you cannot probe all the way down to its
Classical Radius.
When we have probed as deeply as we can with our current
experiments, down to about 10^(-16) cm at about 100 GeV energies, we
have found pointlike Musa/Ganesha
Electrons, Quarks, and Gluons.
Gordon Kane describes what "pointlike" means in this context, in
his book Modern Elementary Particle Physics, Updated Edition, by
Gordon Kane (Addison-Wesley 1993 pages 217-221):
"... The basic quantity we need to organize the data is the cross
section [ sigma(point) ] for e+ e- -> f fbar where f is a
point-like spin 1/2 fermion [and fbar is the antiparticle of
f]. By comparison of the actual cross section with the point-like
one, we want to test whether any given fermion is point-like. ...
[equation 19.7] d sigma(point) / d OMEGA = ( Qf^2 alpha^2
/ 4 s ) ( 1 + cos^2(theta) )
... [Section] 19.1 Are Quarks, Lepton, and Gluons
Point-Like? How well has the point-like nature of quarks,leptons, and
gluons been tested? At LEP, the processes e+ e- to e+ e-, e+ e- to
mu+ mu-, and e+ e- to tau+ tau- have been studied for a center of
mass energy up to MZ [about 90 GeV], and behave to an
accuracy of order 1% as expected from equation 19.7 as functions of s
and theta. The same result holds for e+ e- to q qbar . It is
particularly impressive here, since the quarks are produced as jets,
as described in Chapter 15. The jets have the 1+cos^2(theta) expected
from equation 19.7 if they are spin 1/2 fermions. For example, the
number of jets pointing at 0 degrees or 180 degrees is twice that
pointing at 90 degrees. The sizes of the cross sections are given
correctly for the fractional electric charges normally assigned to
the quarks. The c quark and b quark can be identified from their weak
decays, so the cross sections for e+ e- to c cbar and e+ e- to b bbar
have been studied to MZ as well, and are point-like. ... For
comparison, the cross section for e+ e- to p pbar will be about
10^(-9) of the point cross section at sqrt(s) = 150 GeV because the
proton is not point-like. How can these results be interpreted?
Historically, structure has always appeared when the available
"particles" were probed with projectiles having energies small
compared to the mass - for molecules, atoms, nuclei, and nucleons.
Here the energies of the probes are of two or more orders of
magnitude larger than the masses and no evidence for structure has
appeared. Ultimately it will remian an experimental question, but it
is already clear that quarks and leptons cannot have structure in the
same sense that atoms or nuclei or protons had structure. The same
result holds for photons and gluons and W+/- and Z0 bosons, whose
cross sections are all point-like. ..."
Tony Smith's Home Page
......





