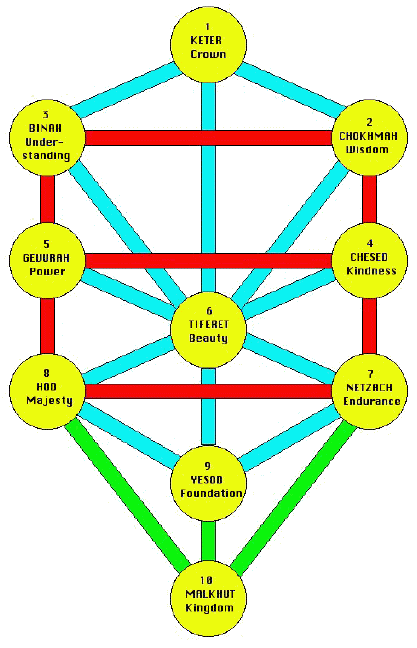
This diagram of the Sefirot (and the English words for each vertex) come from a figure on page 193 of the book The Jew in the Lotus, by Rodger Kamenetz (HarperCollins 1994). I added the 3 colors for the lines. There exist other, slightly different, arrangements of the 22 lines, such as those shown on the web pages of Michael Graffam.
The Sefirot has some structure that is similar to the structure of Singularities.
The 22 lines can be put in correspondence with the 22 letters of the Hebrew alphabet.
The Hebrew alphabet has 22 letters (compare the 0 plus 21 Major Arcana of the Tarot); 3 are Elementary (compare quaternion imaginaries)(green Sefirot lines); 7 are Double (compare octonion imaginaries)(red Sefirot lines); and the remaining 12 are Simple (compare the 12 Branches)(cyan Sefirot lines); as shown in this table that lists a correspondence with ASCII characters that can be used in an internet version of the Torah:
Elementary Double Simple Final ALEF A BET B GIMEL G DALET D HEY H VAV V ZAYIN Z HET X TET + YUD Y KAF K LAMED L MEM M NUN N SAMEH $ AYIN O PEH P TZADE C QOF Q RESH R SHIN/SIN S TAV T KAF SOFIT k MEM SOFIT m NUN SOFIT n PEH SOFIT p TZADE SOFIT c
The 12 Simple letters correspond to the 12 vertices (both concave and convex) of the Mogan David:
/\ ____/__\____ \ / \ / \/ \/ /\ /\ /__\____/__\ \ / \/
In addition to the 22 Hebrew letters,
there are 5 Finals that also appear in the Torah sequence.
Stan Tenen is studying relationships between
the 22 Hebrew letters and the 5 Final,
and has shown how the 27 letters correspond to a Magic Cube.
The Sefirot has 3+7 = 10 vertices (compare the 10 Stems).
It is basically 3 columns:
x
x x
x x
x
x x
x
x
3 vertices - 4 vertices - 3 vertices
The pattern of 10 vertices could correspond to
the 10-dimensional Poincare group or
the 10-dimensional compact Spin(5) deSitter group,
by letting
the left column represent Spin(3) rotations,
the right column represent Spin(3) Lorentz boosts,
and
the central column represent 4-dimensional spacetime.
The central column has a 1+3 structure like spacetime,
with the top vertex representing time.
Consider the 8 vertices:
x
x x
x x
x
x x
Now consider the octonions, with basis {1,i,j,k,E,I,J,K}.
The 8-vertex set could represent the octonions:
1
i I
j J
E
k K
This part of the Sefirot could represent the octonion
vector representation space
of the D4 Le algebra Spin(8) of the D4-D5-E6-E7 physics model.
What about the other two vertices, F and G?
1
i I
j J
E
k K
F
G
If they are added to the octonionic 8 vertices,
you get the 10-dimensional vector representation space
of the D5 Lie algebra Spin(10) of the D4-D5-E6-E7 physics model.
The D5 Lie algebra Spin(10) is 45-dimensional,
representing all possible connecting lines
between the 10 vertices of the Sefirot.
The traditional Jewish Rabbinical Kabbala uses only 22
of the 45 lines that connect Sefirot vertices.
Those 22 lines, plus the 10 vertices,
form a total of 32 things,
called the 32 Paths of Wisdom.
The 32 Paths of Wisdom correspond to
the 32-dimensional full spinor representation of D5 = Spin(10).
Adding the 45 dimensions of the adjoint representation of D5
and the 32 dimensions of the full spinor representation of D5
plus 1 more dimension (mathematically, a complex U(1)),
gives
the 45+32+1=78-dimensional Lie algebra E6
of the D4-D5-E6-E7 physics model.
Why does the Kabbala use only 22 lines ?
There may be many reasons.
One reason may be to show underlying Octonionic structure:
2 lines connect i to j and j to k
orienting the associative triangle ijk;
6 lines connect ijk to E and E to IJK
defining the coassociative square EIJK
whereby E acts to mirror ijk and IJK;
3 lines connect ijk to IJK
identifying the triangle subspace
of the EIJK coassociative square;
2 lines connect I to J and J to K
orienting the triangle subspace
of the EIJK coassociative square;
2 lines connect ij to JI
defining i and j as
the algebraically independent generators of the quaternions;
3 lines connect 1 to iEI
defining the associative triangle iEI;
2 lines connect E to F and F to G
defining EFG as a mirror of IJK and of ijk; and
2 lines connect k to F and F to K
orienting the triangle kFK related to
the associative triangle kEK.
What about the 23 lines that are not shown on the Sefirot?
They also indicate octonionic structure:
Since i and 1 form the complex numbers,
there is a line from i to 1
but the 2 lines from j or k to 1 are omitted;
Since I mirrors i,
the 2 lines from J or K to 1 are omitted;
Since k is not algebraically independent,
the 1 line from k to i is omitted;
Since K mirrors k,
the 1 line from K to I is omitted;
Since k and IJ are in mirror image triangles,
the 2 lines from k to I and from k to J are omitted;
Since K mirrors k,
the 2 lines from K to i and from K to j are omitted;
Since G is not octonion,
and is algebraically dependent on E and F through EFG,
G is connected only to F
and the other 8 lines from G are omitted; and
Since F, also not octonion, is the middle element of EFG,
and E mirrors i and F mirrors j,
the 1 line from F to 1 is omitted,
but is implicitly defined through E.
Since F is algebraically independent of E within EFG,
the mirror property of F is shown by the kFK lines
from F to k and from F to K.
The 4 lines of the iFI and jFJ are omitted,
but are implicitly defined through E.
The 5 implicit lines from F correspond to the 5 Finals.
Added to the 22 explicit Hebrew letter lines,
the full 27-letter alphabet of the Torah sequence is formed.
Since EFG is a mirror of IJK and of ijk,
and
since ijk, the imaginary quaternions, form a 3-sphere S3,
and
since 1 represents a point,
a nice representation of the Sefirot
is by a point and three 3-spheres:
1
S3 S3
S3
What if you expand the quaternionic 3-spheres S3
to octonionic 7-spheres S7 ?
Then you get the configuration:
1
S7 S7
S7
with 1 + 3x7 = 22 vertices,
corresponding to the 22 lines of the Sefirot,
and to the 22 letters of the Hebrew alphabet,
and to the 21 Major Arcana plus 0 of the Tarot,
and to the 21-dimensional Lie algebra Spin(7) plus U(1).
If you cannected all 22 vertices to each other,
you would have 22x21/2 = 231 lines,
corresponding to pairs of the 22 Hebrew letters.
Stan Tenen is studying relationships between
the 22 Hebrew letters and the 5 Finals.
If you add the 5 final letters to the configuration,
one to each of the three 7-spheres
to make three octonions, OX, OY, and OZ,
and
the other two to the 1
to make three real numbers a, b, and c,
you get the configuration:
a,b,c
OX OY
OZ
that has 3 + 3x8 = 27 vertices.
To see more about this algebraically,
represent the 5 Final letters by bars and dots,
two letters being
represented by solid and broken bars: ___ _ _
and
three letters being
represented by 3 sets of dots: . .. ...
If the 22 Hebrew letters are broken into 3 groups
of 8, 6, and 8 letters,
and if the two Final lines are added to make 5 groups
of 1, 8, 6, 8, and 1 letters including 2 Finals,
those 24 letters and Finals represent
the 24 vertices of a 24-cell,
or,
equivalently, 3 octonions.
If the three Final sets of dots are added,
and are taken to represent 3 real numbers,
then
the resulting 27-letter Hebrew alphabet represent
the 3x3 Hermitian Octonion Matrices
a OX OZ
OX* b OY
OZ* OY* c
(where * denoted octonion conjugation)
of the exceptional Jordan algebra J3(O),
and
correspond to the 27 lines on a cubic surface,
whose symmetry is
that of the Weyl group of the 78-dimensional E6 Lie algebra,
corresponding to the 78 Tarot cards.
The Sefirot has some structure that is similar to the structure of Singularities:
Beauty/Tiferet has 8 lines, and the bimodal singularities have 8 infinite series plus 14 (corresponding to the Lie group G2) exceptional families.
Yesod/Foundation has 3 lines (plus 1 other line to Malkhut/Kingdom), and there are 3 H singularities (H2, H3, H4) plus the I2(k) singularities.
Malkhut/Kingdom has 3 lines, and the simple singularities are A, D, and E (if the E is the central line up to Yesod/Foundation, it is a connection between E and H).
The 6 outer vertices, 2 sets of 3 (like ijk and IJK of the 1ijkEIJK octionions, are connected to each other by a network of 7 lines (like the 7 imaginary octonions).
According to the book Singularities of Differentiable Maps, Volume I, by V. I. Arnold, S. M. Gusein-Zade, A. N. Varchenko (Birkhauser 1985):
"... a non-Jew who studies the details of the seven Noahide laws, which are incumbent on him, deserves the honors due a Kohen Gadol (Sanhedrin 59a). The study of the seven Noahide laws may lead him to study most of the precepts of the Torah (Meiri to Sanhedrin 59a; see Responsa, Rama section 10). ...
... Noahide Laws - the seven commandments given to Noah and his sons, which are binding upon all gentiles. These laws include the obligation to have a body of civil law, and the prohibitions against idolatry, immorality, bloodshed, blasphemy, stealing and robbing, and eating limbs from a live animal. ...". (From Talmud Bavli / Tractate Chagigah, The Gemara, The ArtScroll Series / Schottenstein Edition, Mesorah Publications Ltd. (1999) 13a 3)
...
...