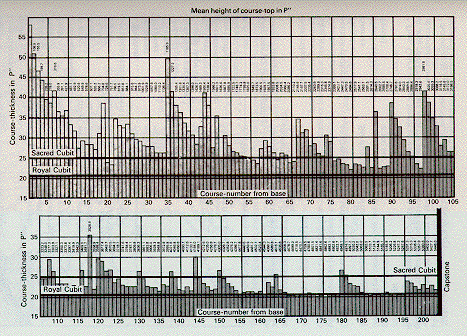
Here, the units of measurement are
the Primitive Inch (PI = 2.54268 cm)
and the Royal Cubit (RC = 20.6066 PI, or 52.396 cm).
The Royal Cubit was a fundamental unit of measurement
used in ancient times. The chart shows that
all the courses of the Great Pyramid
are at least 1 RC thick.
The Primitive Inch was introduced as a convenient unit
for correlating the dimensions of the Great Pyramid.
A Primitive Inch is
very close to a British Inch (1 PI = 1.00106 BI).
Another unit shown,
the Sacred Cubit (SC = 63.56725 cm = 25 PI),
was introduced by Isaac Newton
to show relationships among
the Great Pyramid, the Temple of Solomon, and
the size of the Earth (of radius 10,000,000 SC).
If you number the courses starting at the top
rather than the base, and if you count the capstone
as course number 0, then the base is course number 203.
It is clear from the chart that some of the courses are
distinctively thick. Starting at the top,
these 13 courses are thicker than any preceding course, and (except for 0 and 1) thicker than any adjacent course: Course Number from top = 204 - number from bottom 0 1 2 4 8 24 54 60 86 106 (Upper Shaft outlets are 100(S), 101(N)) 160 (Upper Chamber floor is 154) 169 (top of Aurora-parallelogram) 203 (base of Great Pyramid is 203) These 11 courses are local peaks, thicker than any other within 3 courses: 32 40 66 74 96 114 (Mid Chamber Outlets would be at 113, 114) 118 130 137 145 (Upper Chamber roof) 185 (Mid Chamber floor is 179)
Jim Branson (e-mail: knowhow@cyberhighway.net) has noted that the course thickness variations may not be arbitrary. Here is a modified version of his idea: Consider dividing a musical octave into 12 semitone intervals of the 12th root of 2. Then use the thickness of the thinnest courses, 1 RC = 20.6066 PI, as the fundamental unit, and semitone ratios to get a range of thicknesses. You can then fit the course thicknesses to the semitone thicknesses. To illustrate how it works, the following table gives a fit for the lowest 24 courses. Other courses can be done similarly. For example, course number 7 is about 41.21 PI thick, and so is 1 octave, or 12 semitone steps, away from the fundamental. The table also shows the 7 Platonic notes of the octave, with the Platonic ratio given for those notes. The table is approximate, in that calculations have round-off error, and in that course thicknesses are approximated. Semi Plato's Steps Ratios Ratio Thickness Courses 0 1 1 1 RC = 20.6066 13 1 1.0595 21.83 2 9/8 1.125 23.18 20 3 1.1893 24.51 19 4 81/64 1.266 26.08 17 5 4/3 1.333 27.48 6 1.4145 29.15 14,15,16,18 7 3/2 1.500 30.91 8 1.5878 32.72 12,22,23,24 9 27/16 1.688 34.77 9,11,21 10 1.7824 36.73 8,10 11 243/128 1.898 39.12 5,6 12 2 2 2 RC = 41.21 7 13 2.1198 43.68 4 14 18/8 2.250 46.36 3 15 2.3796 49.04 16 162/64 2.531 52.16 2 17 8/3 2.667 54.95 18 2.8301 58.32 1 19=12+7 3 3 3 RC = 61.82 Since no course is thinner than course 13 at 1 RC = 20.6066 PI and the bottom course 1 is the thickest at about 58.32 PI, you can fit all the courses within 18 steps of the fundamental. Since the bottom 24 steps are thicker than average, the table is NOT representative of all the courses. You can go to the gif image near the top of this page to see thicknesses all the courses in the Great Pyramid. Here is a similar table for the Chinese 5-note octave, with the 5-note equal tempered value of the ratio given after the ratio, thickness calculated by ratio, but no course numbers given: Steps Ratio Equal Tempered Thickness 0 1 1 1 RC = 20.6066 1 8/7 1.15 23.55 2 4/3 1.32 27.48 3 3/2 1.52 30.91 4 7/4 1.74 36.06 5 2 2.00 2 RC = 41.21 6 16/7 2.30 47.10 7 8/3 2.64 54.95 8=5+3 3 3.03 3 RC = 61.82 There is also a Chinese 53-note octave, with 84 steps to the Perfect Fifth in the second octave, developed by King Fang about 40 BC, but I have not written a table for it. Some musical/mathematical references used here are: The Music of the Spheres, by Jamie James (Copernicus of Springer-Verlag, 1993); and Edward Dunne's web page on Pianos and Continued Fractions. It would be interesting to set the fundamental and intervals to a musical scale and play the music of the Great Pyramid courses.
Here is some more interesting geometry: The Aurora is a unit of area, 10,000 square Royal Cubits. At the center of the base of the masonry core of each face of the Great Pyramid is
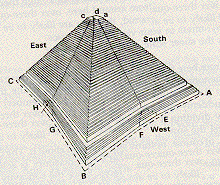a flat triangle related to the concavity of the face.
/ \
/________________________\ course 169
/ /\ \
/____________/__\____________\ course 203
The base of the triangle is at course 203, the base course,
and the top of the triangle is at course 169,
the 35th course from the base.
The sides of the triangle are
parallel to the sides of the pyramid,
so the triangle divides the face
into two mirror-image parallelograms
with the center of course 169 as top,
course 203 as bottom,
a triangle side for one side, and
a pyramid side-segment for the other side.
Each parallelogram has altitude 1160.9 PI
and base 3652.4 PI, giving an area
of 56.4 RC x 177.3 RC = 9,999.7 RC^2 = 1 Aurora.
Symbolically: Since the Great Pyramid is a Square Pyramid, the 24 courses that are distinctly thick might represent the Square Pyramidal Number SPN(24) = 1 + 4 + 9 + 16 +...+ 24^2 = 4900 = 70^2 the only Square Pyramidal Number that is itself a square. In 24 dimensions, it has the elegance of the 2-dimensional 3,4,5 triangle of 9+16 = 25 that represents the slope of the Second Pyramid. (Thanks to Herm Sorem (herms@ix.netcom.com) for correcting a typo I had made on SPN(24).) The capstone, course 0, might represent the Integers; course 1 might represent the Real Numbers; course 2 might represent the Complex Numbers; course 4 might represent the Quaternions; course 8 might represent the Octonions; and course 24 might represent the Leech Lattice.
What was the Capstone of the Great Pyramid? The capstone of the Great Pyramid has been missing so long that there are no reliable records of what it looked like. It is possible that it was a small pyramid, or pyramidion, on top of an obelisk set on the present square top of the Great Pyramid about 264.5 RC (one RC = 0.524 meters) above its base. If the pyramidion were constructed so that its top was at the geometric apex of the Golden Ratio Pyramid, the top of the pyramidion would have been roughly 282 RC above the base of the Great Pyramid, with a pyramidion/obelisk height of roughly 17.5 RC, or roughly 9.2 meters. However, it is possible that the pyramidion/obelisk could have been more than 9.2 meters high. If it were 25.6 meters or about 48.8 RC, roughly comparable to the height of the obelisk from Luxor, now in Paris at the Place de la Concorde in Paris, then the total height from the base of the Great Pyramid would have been about 313.3 RC, or 31.3 RC above the geometric apex height of about 282 RC, or 10/9 of the geometric height of about 282 RC, or, from the point of view of the web page of John Miller, the Golden Ratio geometric apex height would be 10% less than the height of the pyramidion/obelisk, and the top of the pyramidion/obelisk would then be at the vertex of a half-octahedral pyramid with slope angle about 54.7356 degrees.