Cl(1,3) from Cl(1,2) and Cl(1,1)
is an important structure in many physics theories, including the D4-D5-E6-E7-E8 VoDou Physics Model. There are two Clifford Algebras for Minkowski Spacetime:
Cl(3,1) = M(4,R) = 4x4 Matrix Algebra over the Real Numbers for signature (3,1); andCl(1,3) = M(2,Q) = 2x2 Matrix Algebra over the Quaternions for signature (1,3).
They are not isomorphic. The key to understanding how they work is the isomorphism
of the 4x4 Matrix Algebra over the Real Numbers with the tensor product of two Quaternionic spaces.
To see how that isomorphism works, let { 1, i, j, k } be a basis for Q. Since Quaternionic Multiplication is not commutative, you have to distinguish between Left-Multiplication and Right-Multiplication.
Let { 1, iL, jL, kL } denote Left-Multiplication by 1, i, j, and k, and let { 1, iR, jR, kR } denote Right-Multiplication by 1, i, j, and k. Left- and Right-Multiplication by 1 is the same, but by 1, j, and k it is different.
Let QL denote the Left-Multiplication actions whose basis is { 1, iL, jL, kL } and let QR denote the Right-Multiplication actions whose basis is { 1, iR, jR, kR }. Note that QL and QR have in common the real axis spanned by { 1 }.
Since QL is isomorphic to QR and both are isomorphic to Q, describe the tensor product Q x Q by the tensor product QL x QR, so that the basis elements of Q x Q are formed from
or, in other words:
iL, jL, kL,
iR, jR, kR,
iL iR, iL jR, iL kR,
jL iR, jL jR, jL kR,
kL iR, kL jR, kL kR }
These 16 elements are isomorphic to M(4,R), or, in Geoffrey Dixon's terminology, to the full adjoint action QA of the Quaternions. M(4,R) has graded structure 1 4 6 4 1 and is generated by the 4 vector basis elements, which can be written as
1 0 0 0 0 1 0 0 0 0 -1 0 0 0 0 -1 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 1 0 0 -1 0 0 -1 0 0 1 0 0 0 0 0 0 1 0 0 1 0 0 -1 0 0 -1 0 0 0
In this representation, the scalar identity of M(4,R) is
1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1
and the pseudoscalar of M(4,R) is
0 0 -1 0 0 0 0 1 1 0 0 0 0 -1 0 0
M(2,Q) = Cl(1,3) is generated by its 4 vector generator basis elements
1 0 0 -1 0 i i 0 0 j j 0 0 k k 0
In this representation, the scalar identity of M(2,Q) is
1 0 0 1
and the pseudoscalar of M(2,Q) is
0 1 -1 0
If you tensor Cl(3,1) with itself, you get M(4,R) x M(4,R) = M(4x4,RxR) = (since RxR = R) = M(16,R) = Cl(0,8), which is the basis of the D4-D5-E6-E7-E8 Vodou Physics Model and is the basis of the 8-fold Periodicity of Real Clifford Algebras and of Homotopy.
If you tensor Cl(1,3) with itself, you get M(2,Q) x M(2,Q) = M(2x2,QxQ) = (since QxQ = M(4,R)) = M4,M(4,R) = M(16,R) = Cl(0,8), which is also the basis of the D4-D5-E6-E7-E8 VoDou Physics Model and is also the basis of the 8-fold Periodicity of Real Clifford Algebras and of Homotopy.
there is the question:
John Baez, on the usenet group sci.physics.research, said:
Note that Spin(-+++) = Spin(+---) = SL(2,C), so that you can't use the Spin group to tell which is the right one, so look at the Clifford algebra from which the Spin group is derived. The Clifford algebras of candidate physical spacetimes are:
Cl(-+++) = Cl(1,3) = M(2,Q) the 2x2 quaternionic matrix algebra.
Both of them are Clifford algebras with a real 4-dim vector space, and graded structure
Since all these spaces are real, the bosons in both of them are real.
However, the fermions should correspond to half-spinors, with the fermion particles being +half-spinors and the fermion antiparticles being mirror image -half-spinors.
For Cl(+---) = Cl(3,1), the full spinor space (minimal ideal of the Clifford algebra) is 1x4 real column of the 4x4 real matrix and each half-spinor space is 1x2 real column, so a fermion half-spinor would be real.
For Cl(-+++) = Cl(1,3), the full spinor space (minimal ideal of the Clifford algebra) is 1x2 quaternionic column of the 2x2 quaternionic matrix and each half-spinor space is 1x1 quaternion column, or, in other words, a fermion is a quaternion.
Therefore, if "... fermions are quaternionic and bosons are real ..." then
Some interesting structure of Cl(1,3) is shown by
modifying the construction of Minkowski Cl(3,1) = R(4) from Cl(2,0) = R(2) and Cl(1,1) = R(2) of Dennis W. Marks, Larry J. Arbuckle, James Baugh, David Ritz Finkelstein, Jason Looper, and Heinrich Saller as described by Dennis Marks in his talk at SESAPS 2002 at Auburn
to a construction of Minkowski Cl(1,3) = Q(2) from Cl(0,2) = Q and Cl(1,1) = R(2).
In the notation below:
Cl(0,2) = Q
Note that the quaternions are natural variables for a Dirac equation in 2-dimensional Eucliudean space with Planck constant factor Ih.
basis (1x1 quaternion):
1 i j k
z y Ih
2x2 complex Pauli representation basis:
1 0 0 1 1 0 0 i
0 1 1 0 0 -1 -i 0
Cl(1,1) = R(2)
Note that (1,1) signature is that of 1+1=2-dim spacetime with space/time conversion factor Ic which also acts as Planck constant factor Ih for a Dirac equation in 2-dimensional Minkowski space.
basis (2x2 real):
1 0 0 -1 1 0 0 1
0 1 1 0 0 -1 1 0
t x Ic
Cl(1,1) x Cl(0,2) = Cl(1,3) = Q(2)
Note that the 2-dim Ic and Ih factors map to middle-grade bivectors while the factor Ich that is effective in 4-dim is the pseudoscalar and that Ich acts as both space/time conversion factor and Planck constant factor.
basis
1 0 0 -1 1 0 0 1
0 1 1 0 0 -1 1 0
i 0 0 -i i 0 0 i
0 i i 0 0 -i i 0
j 0 0 -j j 0 0 j
0 j j 0 0 -j j 0
k 0 0 -k k 0 0 k
0 k k 0 0 -k k 0
or,
taking into account
1 2 1 1ijk
1 2 1 R(2) matrices
1 2 1
2 4 2
1 2 1
1 4 6 4 1
with graded structure:
---------------------------------------
1 0
0 1
---------------------------------------
i 0 j 0
0 i 0 j
z y
0 -1 1 0
1 0 0 -1
t x
---------------------------------------
k 0
0 k
Ih
0 -i j 0 0 -i j 0
i 0 0 -j i 0 0 -j
0 1
1 0
Ic
--------------------------------------
0 i 0 j
i 0 j 0
0 -k k 0
k 0 0 -k
--------------------------------------
0 k
k 0
Ich
--------------------------------------
In this case of Cl(1,3) = Q(2),
the full spinor space would be 8-dimensional:
1
0
i
0
j
0
k
0
and
0
1
0
i
0
j
0
k
Each half-spinor space would be 4-dimensional
with quaternionic structure
and would have a triality-like isomorphism
with the vector space of Cl(1,3).
That triality would correspond to the triality of Cl(1,7) = R(16)
with dimensionality 2^8 = 256 = 16x16
and
8-dimensional half-spinors
and
graded structure
1 8 28 56 70 56 28 8 1
that is used in the D4-D5-E6-E7-E8 VoDou Physics model.
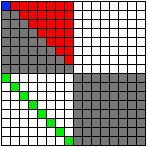
The D4-D5-E6-E7-E8 VoDou physics model is based on representations of Spin(0,8). In 8 dimensions, Cl(0,8) = M16(R) the 16x16 real matrices
The 1-dimensional scalar 0-grade subspace is represented as the blue square. It is a 1-dimensional part of the symmetric part of the upper left 8x8 diagonal subspace. The 8-dimensional vector 1-grade subspace is represented as the green squares. It is part of the lower left 8x8 off-diagonal subspace. The 28-dimensional bivector 2-grade subspace is represented as the red squares. It is the antisymmetric part of the upper left 8x8 diagonal subspace. This accounts for the 1 8 28 graded elements of the 1 8 28 56 70 56 28 8 1 = 256-dim Cl(0,8). The 56-dimensional trivector 3-grade subspace is represented as the white squares in the lower left quadrant. In the full 8-dimensional theory, the 56 trivectors are related to the structure of 3+1=4-dimensional subspaces of 1+7=8-dimensional spacetime that are connected with the E8 HyperDiamond lattice links that are (normalized) sums of 4 of the basis octonions. To reduce the dimension of spacetime to 1+3=4 dimensions, an associative 3-form is used. This effectively fixes a particular trivector, so the 56 trivectors do not play a dynamical role in the 4-dimensional phase of the D4-D5-E6 model. Here and now, we do not have the technology to do experiments that could test the structure of the full 56-dimensional trivector sector. The 70 4-vectors in the 4-grade subspace are reducible to two sets of 35 4-vectors each. One set of 35 4-vectors is represented as the grey squares in the upper left quadrant. They are the symmetric parts of the upper left 8x8 diagonal subspace, remaining after taking out the 1-dimensional scalar 0-vector Higgs scalar. The 1-dimensional scalar 0-vector representing the Higgs scalar can be thought of as the trace of the full symmetric 1+35=36-dimensional space of symmetric 8x8 real matrices. The 35 4-vectors are the traceless symmetric 8x8 matrices. They are related to the coassociative 4-form that is fixed in the dimensional reduction process to determine the internal symmetry space. At our low energy levels, below the Planck-scale at which dimensional reduction occurs in the D4-D5-E6 model, the 35 4-vectors do not play a dynamical role that we can test experimentally here and now. However, they show that the Higgs mechanism is related fundamentally to BOTH the particles and fields of the internal symmetry space and the spacetime of conformal MacDowell-Mansouri gravity.
According to Dennis W. Marks, in his paper A Binary Index Notation for Clifford Algebras (revised 27 February 2003):
"... we define the n x n co-identity matrix asJ_n = e_(2^n - 1) = e_(1 ... n ones ...1)
... Duality operations generate isomorphism between grades k and n-k. There are several different duals, including
- the Clifford dual, which we will write as e_m*, defined ... as e_m* = e_m J_n,
- and the Hodge dual, which we will write as m_e_*, defined as m_e_* = (m_e) J_n = (-1)^( k_m ( k_m - 1 ) / 2 ) e_m J_n = (-1)^( k_m ( k_m - 1 ) / 2 ) e_m*.
- ... A dual distinct from the preceding duals is introduced by bit inversion that maps e_m -> e_mbar , where mbar is the bit inverse of m ... In particular, bit inversion transforms vectors (grade 1) ... into covectors (grade n-1) ...
The bit inverse of the bit inverse is the original element: e_mbarbar = e_m.
For the various duals involving J_n, the dual of the dual of e_m is +/- e_m ...
The duals involving J_n also ...[depend on]... the handedness of the base coordinate system, because J_n changes sign with the swapping of two of the bases.
Bit inversion does not ...[ depend on the handedness of the base coordinate system ]...
Complementarity between space-time and momentum-energy is achieved by bit inversion, which interconverts between position representation and momentum representation.
Treating momentum as a Clifford covector has the virtue of automatically enforcing the Heisenberg commutation relation as a consequence of the commutation and anti-commutation propeerties of the Clifford elements. ...".
In the case of 4-dimensional physical space-time, with Clifford algebra Cl(1,3) and graded structure
1 4 6 4 1
Marks's bit inversion complementarity acts on the middle-grade 6-dimensional bivectors (grade 2) as a map of the 6-dimensional Lorentz Lie Algebra Spin(1,3) = Spin(3) x Spin(3) into itself, acting as an isomorphism between the 3-dimensional Spin(3) rotation Lie algebra (rotations of positions with x, y, and z components) and the 3-dimensional Spin(3) boost Lie algebra (transformations of momenta with tx, ty, and tz components).
In the case of 8-dimensional space-time, with Clifford algebra Cl(1,7) and graded structure
Since the 70 decomposes into two 35s, just as the Cl(1,3) 6 decomposes into two 3s,
you can write the graded structure as
1 8 28 56 (35+35) 56 28 8 1
where the blue 1 8 28 56 35 have the 8-position-related physical interpretation given above, and Dennis Marks's bit inversion gives a complementarity between the position-related blue 1 8 28 56 35 and the corresponding momentum-related Clifford co-multivectors of the red 35 56 28 8 1. The bit inversion complementarity can be visualized in terms of the figure
as a mapping of the two left-hand quadrants (8-position-related) onto the two right-hand quadrants (8-momentum-related) by reflection through the center (origin) of the figure.
The relevant Duality Structure can be seen in such physical concepts as Type IV(2) Domains, Hyperspace, Black Holes, Wavelets, and Conformal SpaceTime.
What about the SPINOR representations? To see the two 8-dimensional half-spinor spaces of Cl(0,8), look at the even subalgebra Cle(0,8):
The minimal-left-ideal column 8-dimensional half-spinors are the blue-green columns, one each in the two 8x8 diagonal subspaces of Cle(0,8). The minimal-right-ideal row 8-dimensional half-spinors are the yellow-green rows, one each in the two 8x8 diagonal subspaces of Cle(0,8). The two 8-dimensional half-spinor spaces and the 8-dimensional vector space of Cl(0,8) are all isomorphic to each other. This is Spin(0,8) TRIALITY, and is evident in the Dynkin diagram of Spin(0,8):
The 4 Spin(0,8) representations of the Dynkin diagram are: the green point is the vector, the two blue points are the two (left-ideal column) half-spinors, and the red center is the 28-dimensional adjoint.
Along with the scalar representation, these representations are used to build the 8-dimensional Lagrangian of the D4-D5-E6 physics model: The vector representation is the 8-dimensional spacetime over which the Lagrangian density is integrated. The adjoint representation gives the curvature term and (through the covariant derivative) interactions with spinor fermion and scalar particles. The half-spinor representations give the spinor fermion term. The scalar representation gives the scalar term. Path-integral quantization can produce gauge-fixing and ghost terms.
To make connection with observable physics in our regime, far below the Planck energy of 10^19 GeV, the 8-dimensional nonassociative octonionic spacetime must be reduced to a 4-dimensional associative submanifold.
Since the more realistic Minkowski Physical SpaceTime with -+++ Signature has Quaternionic Structure, a useful Clifford path is this Clifford Path that is Quaternionic from Cl(3,5) through Cl(2,4) to Cl(1,3) and from Cl(2,6) through Cl(2,5) and Cl(2,4) to Cl(1,3):
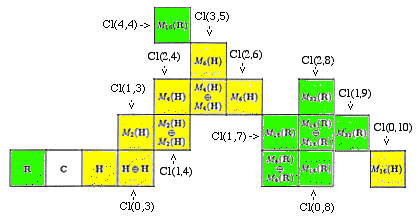
In the D4-D5-E6-E7-E8 VoDou Physics model, D5 is taken to be SL(2,O) = Spin(1,9), and spinors are R16 + R16 of Cle(1,9) = Cl(1,8),
where Cle(p,q) = Cl(p,q-1) and Cle(p,0) = Cl(0,p-1)
The D4 can initially be taken to be Spin(0,8), or, with the same Clifford algebra, Spin(1,7) or Spin(4,4). Dimensional Reduction from 8 to 4 dimensions introduces the subspace substructure of Quaternionic Physical SpaceTime in Octonionic Vector Space.
The (1,7)-dimensional RP1 x S7 = S1 x S7 = U(1) x S7 spacetime of the D4-D5-E6-E7-E8 VoDou Physics model prior to dimensional reduction can be represented by Quaternionic Projective 2-space QP2.
Atiyah and Berndt say in their paper Projective Planes, Serveri Varieties, and Spheres, math.DG/0206135, the S1 x S7 considered as QP2 breaks down into two parts:
Therefore, dimensional reduction changes Real M(16,R) of Cl(0,8), Cl(1,7), and Cl(4,4) to the Quaternionic M(8,Q) of Cl(2,6) or Cl(3,5).
Cl(2,6) = M(8,Q) Spin*(8) = Spin(2,6) Cl(2,5) = M(4,Q)+M(4,Q) Spin(2,5) Cl(2,4) = M(4,Q) Spin(2,4) = SU(2,2)
Spin(2,4) = SU(2,2) is the connected component with identity of the Conformal(1,3) Group of Minkowski SpaceTime. Since both 1+1 and 3+1 are even, Conformal(1,3) has 4 components, not 2 components as for Conformal(p,q) where p+1 and/or q+1 are odd. U(2,2) = U(1)xSU(2,2) corresponds to compact U(4) = U(1)xSU(4), the compact isotropy space of the 12-dimensional rank-2 symmetric spaces Spin*(8) / U(4) (non-compact) and Spin(8) / U(4) (compact).
Cl(1,4) = M(2,Q)+M(2,Q) Spin(1,4) = Sp(1,1)
Spin(1,4) is the connected component with identity of the deSitter Group of Minkowski SpaceTime. Although the MacDowell-Mansouri mechanism, as originally formulated, produced gravity from anti-deSitter Spin(2,3) = Spin(0,5) = Sp(2), this Quaternionic chain uses, instead of Sp(2), Sp(1,1) = Spin(1,4).
Cl(1,3) = M(2,Q) Spin(1,3)
Spin(1,3) is the connected component with identity of the Lorentz Group of Minkowski SpaceTime.
Cl(0,3) = Q+Q Spin(0,3) = Sp(1) = SU(2) = S3 Cl(0,2) = Q Spin(0,2) = U(1) Cl(0,1) = C Spin(0,1) = Z2 Cl(0,0) = R Spin(0,0) = I
(Much of the above is taken from Ian Porteous's book Clifford Algebras and the Classical Groups (Cambridge 1995).)
The path from Cl(1,7) through Cl(2,4) to Cl(1,3) can also be seen from the viewpoint of spinor fermions of the D4-D5-E6-E7-E8 VoDou Physics model:
Half-Spinors for 16x16 real matrix Cl(1,7) are 1x8 real column vectors
which correspond to first-generation fermion particles:
Octonion Fermion
Basis Element Particle
1 e-neutrino
i red up quark
j green up quark
k blue up quark
I red down quark
J green down quark
K blue down quark
E electron
Full Spinors for 4x4 quaternion matrix Cl(2,4) are
1x4 quaternion column vectors:
q1
q2
q3
q4
which are reducible to two Half-Spinor mirror image
1x2 quaternion column vectors:
q+1
q+2
q-1
q-2
Since each of these is a 4-dimensional quaternion,
if you let the q+ be fermion particles
and the q- be fermion antiparticles,
you have
4 fermion particles for q+1, which can be taken to
be electron, red up quark, blue up quark, and green up quark,
and
4 fermion particles for q+2, which can be taken to
be neutrino, red down quark, blue down quark, and green down quark,
and
4 fermion antiparticles for q-1, which can be taken to
be positron, red up antiquark, blue up antiquark, and green up antiquark,
and
4 fermion antiparticles for q-2, which can be taken to be antineutrino,
red down antiquark, blue down antiquark, and green down antiquark,
so that the quaternionic spinors of Cl(2,4) correspond directly
to the fermions of the real spinors of Cl(1,7).
For Cl(1,3) the 2x2 quaternionic matrices have Full Spinors
that are 1x2 quaternion column vectors.
Each Half-Spinor space is one quaternion variable,
which has a 1-2 correspondence with first generation fermions,
and also corresponds 1-1 with the (1,3) vector space of
physical Minkowski spacetime,
resulting in a quaternionic version of triality (diluted by
the 1-2 nature of the fermion correspondence) that is
related to the reducibility of the D2 Lie algebra Spin(1,3).
Here are some other useful pathways for the D4-D5-E6-E7-E8 VoDou Physics Model:
or
as a Quaternionic Process involving the Quaternions Q.
Since the tensor product Q x Q = M(4,R) = M(2,R) x M(2,R), the Processes are Physically Equivalent.
and M(2,R) x M(4,R) = M(8,R)
and M(2,R) x M(8,R) = M(16,R)
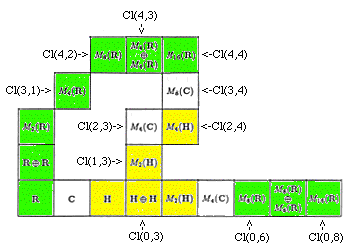
Start with Cl(4,4) = M(16,R), the 16x16 matrices with entries in the Real Numbers, and then represent them as M(2,CSG(4,2)) = M(2,M(8,R)), the 2x2 Vahlen Matrices with entries in the Clifford SemiGroup of the Cl(4,2) Clifford Algebra = M(8,R) of 8x8 matrices with Real entries, which Vahlen Matrices represent the Moebius Transformations of R^(4,2).
The Rotations are 15-dimensional Spin(4,2) = SU(2,2), of the form A x A^(-1) , with matrix form
A 0 0 A
In the D4-D5-E6-E7-E8 VoDou Physics Model, the 15 dimensions of the Rotations are the Spin(4,2) = SU(2,2) Conformal Group of Physical Minkowski SpaceTime,which, through the MacDowell-Mansouri Mechanism, forms Gravity (with Torsion and Parity Violation) plus the Higgs Mechanism.
The Translations are 2+4 = 6-dimensional, of the form x + B , with matrix form
1 B 0 1
The Transversions are 2+4 = 6-dimensional, of the form
1 0 C 1
In the D4-D5-E6-E7-E8 VoDou Physics Model, the 4+4 = 8 dimensions of the Translations and Transversions form the 8-dimensonal SU(3) of the Color Force.
In the D4-D5-E6-E7-E8 VoDou Physics Model, the 2+2 = 4 dimensions of the Translations and Transversions form the 4-dimensonal U(2) of the ElectroWeak Force.
The Dilations are 1-dimensional, of the form x D , with matrix form
sqrt(D) 0 0 1/sqrt(D)
In the D4-D5-E6-E7-E8 Vodou Physics Model, the 1 dimension of the Dilations represent the U(1) Complex Phase of Particle and Force Propagators.
Now consider the R^(4,2) Clifford Algebra Cl(4,2) = M(8,R), the 8x8 matrices with entries in the Real Numbers, and then represent them as M(2,CSG(3,1)) = M(2,M(4,R)), the 2x2 Vahlen Matrices with entries in the Clifford SemiGroup of the Cl(3,1) Clifford Algebra = M(4,R) of 4x4 matrices with Real entries, which Vahlen Matrices represent the Moebius Transformations of R^(3,1).
The Rotations are 6-dimensional Spin(3,1), of the form A x A^(-1) , with matrix form
A 0 0 A
The Translations are 1+3 = 4-dimensional, of the form x + B , with matrix form
1 B 0 1
In the D4-D5-E6-E7-E8 VoDou Physics Model, the 6+4 = 10 dimensions of the Rotations and Translations are the Spin(3,2) anti-deSitter Group of Physical Minkowski SpaceTime,which, through the MacDowell-Mansouri Mechanism, forms Gravity (with Torsion and Parity Violation).
The Transversions are 1+3 = 4-dimensional, of the form
1 0 C 1
In the D4-D5-E6-E7-E8 Vodou Physics Model, the 4 dimensions of the Transversions form the 4 degrees of freedom of the Higgs SU(2) Scalar Particle. They also correspond to the Conformal Moebius transformations involved in torsion-superluminal solutions of Maxwell's equations that may be permit longitudinal photons, thus indicating that such solutions may be related to the Higgs Mechanism.
The Dilations are 1-dimensional, of the form x D , with matrix form
sqrt(D) 0 0 1/sqrt(D)
In the D4-D5-E6-E7-E8 VoDou Physics Model, the 1 dimension of the Dilations represents the Mass/Energy Scale of the Higgs Vacuum Expectation Value, which may represent a measure of the Compressibility of Maxwell's Aether that could give rise to torsion-superluminal solutions of Maxwell's equations that may permit longitudinal photons.
Start with Cl(4,4) = M(16,R), the 16x16 matrices with entries in the Real Numbers.
Since the tensor product Q x Q = M(4,R), M(16,R) = Q x M(4,Q).
The transition from Cl(4,4) = M(16,R) = Q x M(4,Q) to M(4,Q) = Cl(2,4)
is the tensor product by the Quaternions Q,which takes M(4,Q) to M(4,M(4,R)) = M(16,R).
What does the tensor product by Q do to the Spin(2,4) = SU(2,2) part of Cl(2,4) ?
Since the tensor product by Q takes Cl(2,4) to Cl(4,4),
it should take Spin(2,4) = SU(2,2) to Spin(4,4). How does it do that?
Factor the Quaternions Q into a Real Part Re(Q) and an Imaginary Part Im(Q),
and then look at how the tensor product by Q acts on the SU(2,2) that is within Cl(2,4).
The image of this action should contain Spin(4,4), but may contain other stuff that is within Cl(4,4) (or, to be more nearly technically accurate, CSG(4,4)) but is not in Spin(4,4).
Represent Re(Q) by U(1) = S1 and Im(Q) by SU(2) = S3.
Then, regard the tensor product Q x SU(2,2) as
= ( U(2,2) , SU(2) x SU(2,2) )
The first component is just U(2,2) = U(1) x Spin(2,4), which includes the Spin(2,4) of Cl(2,4), and it makes up a 16-dimensional part of 28-dimensional Spin(4,4).
What about the other 12 dimensions of Spin(4,4) ?
They should be in the second component, the tensor product SU(2) x SU(2,2),
but they should only be in the part of it that has Lie Group structure.
To see what part that is, first observe that it contains the Lie Group SU(2) (the first factor)
Then, look at the fibration SU(2,2) / (U(1) x SU(3)) = CHP3 = Complex Hyperbolic Projective 3-space.
Then, regard SU(2,2) as U(1) x SU(3) x CHP3.
Then, since CHP3 is not a Lie Group, disregard it, leaving the Lie Groups U(1) and SU(3).
regard the result of the tensor product by Q of the Spin(2,4) = SU(2,2) part of Cl(2,4) as the 12-dimensional
U(1) x SU(2) x SU(3)
that corresponds to the Standard Model group in the D4-D5-E6-E7-E8 VoDou Physics Model,
plus the U(1) of U(1) x Spin(2,4) = U(2,2) that, in the D4-D5-E6-E7-E8 VoDou Physics Model, corresponds to the Complex U(1) Propagator Phase.
Go from Cl(2,4) = M(4,Q) = M(2,M(2,Q)) = M(2,Cl(1,3)) down to M(2,Q) = Cl(1,3).
M(2,Q) M(2,Q) M(2,Q) M(2,Q)
This step starts with the R^(2,4) Clifford Algebra Cl(4,2) = M(4,Q), the 4x4 matrices with entries in the Quaternions, which are represented as M(2,CSG(1,3)), the 2x2 Vahlen Matrices with entries in the Clifford SemiGroup of the Cl(1,3) Clifford Algebra = M(2,Q) of 2x2 matrices with Quaternion entries, which Vahlen Matrices represent the Moebius Transformations of R^(1,3).
The Rotations are 6-dimensional Spin(1,3), of the form A x A^(-1) , with matrix form
A 0 0 A
The Translations are 1+3 = 4-dimensional, of the form x + B , with matrix form
1 B 0 1
In the D4-D5-E6-E7-E8 VoDou Physics Model, the 6+4 = 10 dimensions of the Rotations and Translations are the Spin(2,3) anti-deSitter Group of Physical Minkowski SpaceTime,which, through the MacDowell-Mansouri Mechanism, forms Gravity (with Torsion and Parity Violation).
The Transversions are 1+3 = 4-dimensional, of the form
1 0 C 1
In the D4-D5-E6-E7-E8 VoDou Physics Model, the 4 dimensions of the Transversions form the 4 degrees of freedom of the Higgs SU(2) Scalar Particle. They also correspond to the Conformal Moebius transformations involved in torsion-superluminal solutions of Maxwell's equations that may be permit longitudinal photons, thus indicating that such solutions may be related to the Higgs Mechanism.
The Dilations are 1-dimensional, of the form x D , with matrix form
sqrt(D) 0 0 1/sqrt(D)
In the D4-D5-E6-E7-E8 VoDou Physics Model, the 1 dimension of the Dilations represents the Mass/Energy Scale of the Higgs Vacuum Expectation Value, which may represent a measure of the Compressibility of Maxwell's Aether that could give rise to torsion-superluminal solutions of Maxwell's equations that may permit longitudinal photons.
The dimensional reduction process starts with the Clifford algebra Cl(0,8) = M16(R), then goes to its even subalgebra Cle(0,8) which is the Clifford algebra Cl(0,7) = M8(R)+M8(R)
+
then goes to its even subalgebra Cle(0,7) which is the Clifford algebra Cl(0,6) = M8(R)
then goes to its even subalgebra Cle(0,6)
which is the Clifford algebra Cl(0,5) = M4(C).
+
The Clifford algebra chain of dimensional reduction is shown below in green:
The chain starts with a real Clifford algebra, Cl(0,8), and proceeds through other real ones until it reaches its end at COMPLEX Cl(0,5) = M4(C). Its even subalgebra is Cle(0,5) = Cl(0,4) = M2(Q) the 2x2 Quaternionic matrix algebra. Since M2(Q) is also the Clifford Algebra Cl(1,3), you get both Euclidean Cl(0,4) and Minkowski Cl(1,3) by taking the even subalgebra of the Cl(0,5) Clifford Algebra of Spin(0,5). In this way, the D4-D5-E6-E7-E8 VoDou physics model allows you to go back and forth by Wick rotation between Euclidean (0,4) and Minkowski (1,3). Further, Cl(0,5) = M4(C) is the complexification of each and every one of the five 4-dimensional real Clifford algebras, shown in blue in the figure above, some of which have Dirac algebra real structure M4(R), and some of which have quaternionic structure M2(Q) (sometimes, as in the figure, denoted M2(H)) In the D4-D5-E6-E7-E8 VoDou physics model the real part of Cl(0,5) = M4(C) describes gravity, and the imaginary part of Cl(0,5) = M4(C) describes the color, weak, and electromagnetic forces, with the Higgs mechanism affecting both sectors. For details, see the references in this home page to the D4-D5-E6-E7-E8 VoDou physics model, as well as the papers linked or cited therein.
Lars Ahlfors, in his paper Clifford Numbers and Moebius Transformations in R^n, published on pages 167-175 of the book Clifford Algebras and Their Applications in Mathematical Physics, Proceedings of NATO and SERC Workshop, Canterbury, Kent, 1985, edited by Chisholm and Common, NATO ASI Series (Reidel 1986), says:
What are Clifford Numbers? Clifford Numbers are the Clifford Semigroup CSG(n) of the Clifford Algebra Cl(n).
Ian Porteous, in his book Clifford Algebras and the Classical Groups (Cambridge 1995), describes the tensor product
and the tensor product
Pertti Lounesto, in his book Clifford Algebras and Spinors (Cambridge 1997), describes the Conformal Compactification of R^(p,q) by Moebius Transformations in terms of the p-sphere Sp and the q-sphere Sq as:
Sp x Sq Z2
Pertti Lounesto's Chapter 16 describes the tensor product relation
The cases of Cl(2,4) = M(2,Cl(1,3)) and Cl(4,2) = M(2,Cl(3,1)) are useful in physics, since Spin(2,4) = Spin(4,2) = SU(2,2) is the Conformal Group of Conformal Transformations of Minkowski Spacetime.
That leads into his discussion of Moebius Transformations and Vahlen Matrices in his Chapter 19, in which he describes them as 2x2 matrices with Clifford entries. Related Conformal Structures may produce GraviPhoton Phenomena.
Pertti Lounesto's Chapter 21 deals with Binary Index Sets and Walsh Functions.
John E. Gilbert and Margaret A. M. Murray, in their book Clifford Algebras and Dirac Operators in Harmonic Analysis (Cambridge 1991), describe the Moebius Transformations, in both Spherical and Hyperbolic Space, by SL(2,CSGn) and by SU(2,CSGn), respectively, where CSGn denotes the Clifford Semigroup of Cl(n). Related Conformal Structures may produce GraviPhoton Phenomena.
Gilbert and Murray describe the Clifford Semigroup of the Clifford Algebra Cl(n) as being made up of all x in Cl(n) such that for each y in R^(n+1) there exists z in R^(n+1) xy = zx', and they they say:
"... Denote by CSG(n) the Clifford semigroup ...CSG(n) = { x y ... z : x, y, z, ... in R^(n+1) } generated by the non-zero elements in R^(n+1), and then denote by CG(n) the Clifford group
CG(n) = { x y ... z : x, y, z, ...in R^(n+1) \ {0} } Of course, CSG(n) = CG(n) u {0}. ...
... [The Clifford norm is denoted by | | and the Clifford operator norm, defined by regarding the Clifford algebra Cl(n) as an algebra of operators on itself, is denoted by || || . They coincide on CSG(n).] ...
For each n = 0, 1, ...
Spin(n+1) = { a in CSG(n) : ||a|| = 1 } ... Now O(n) can be identified with the subgroup of SO(n+1) fixing the subspace R(1,0,...,0) of R^(n+1) ...
... [where Cl(n) has the direct sum graded structure Cl(n) = Cl(0)(n) + Cl(1)(n) + ... Cl(n)(n) and R^(n+1) is regarded as Cl(0)(n) + Cl(1)(n). Let n denote intersection and Cle(n) be the even subalgebra of Cl(n)] ...
For each n = 1, 2, ...,
Pin(n) = { a in CSG(n) : a a* = 1, ||a|| = 1 } Spin(n) = { a in CSG(n) n Cle(n) : a a* = 1, ||a|| = 1 }
... It is well-known that the unit sphere in R^(n+1) ha a multiplicative structure if n = 0, 1, or 3, when it coincides with Pin(1), Spin(2) and Spin(3) respectively. The results above show what to do for larger n:
one takes the unit sphere in the Clifford semi-group CSG(n), not just the unit sphere in R^(n+1). ...".
Gilbert and Murray describe the Periodicity Theorem, saying:
"... For each n > 0 there is a realization of Cl(n+8) as the algebraCl(n+8) = M(16, Cl(n)) of all 16x16 matrices having entries from Cl(n) ...
... For each n > 0 there is a realization of Cl(n+4) as the tensor product
Cl(n+4) = Cl(n) x M(2,Q) = Cl(n) x Cl(4) over R of Cl(n) and M(2,Q) ... [the 2x2 matrices with entries in Q, the quaternions] ...
... two-fold application of [the realization] gives
Cl(n+8) = Cl(n) x M(2,Q) x M(2,Q)
with respect to the usual tensor product of algebras. Since M(2,Q) x M(2,Q) = M(16,R), ... [ ...
Cl(n+8) = Cl(n) x M(16,R) ... ] ...".
Gilbert and Murray describe the Dirac Operator, which is the natural differential operator acting on spinors ( and therefore the natural differential operator for the fermion terms in the Lagrangian of the D4-D5-E6-E7-E8 VoDou Physics model ), saying:
"... A Clifford algebra bundle can be constructed over any Riemannian manifold, but topological obstructions may prevent the construction of Clifford modules. ... the unit sphere in C has two inequivalent spin structures. But the unit sphere in Rn, n > 3, has exactly one spin structure; its principal Spin(n) bundle is diffeomorphic to Spin(n). ... [ for k > 1 ] real projective space RP(4k-1) has two inequivalent spin structures, whereas RP(4k+1) does not have any [ although it is orientable ] ... RP(2k) is not orientable ... [ and, according to Spin Geometry, by H. Blaine Lawson and Marie-Louise Michelsohn (Princeton 1989), CPn is spin iff n is odd and QPn is spin for all n ] ... An oriented riemannian manifold X admits a spin structure if and only if its second Steifel-Whitney class is zero. Furthermore, if w2(X) = 0, then the spin structures on X are in one-to-one correspondence with elements of H1(X;Z2). ]...... h ... will denote ...[ a Cl(n)-module ]... on which there is a representation t of Spin(n) such thatt(a) e_i t(a)^(-1) = s(a) e_i ( 1 < i < n ) for all a in Spin(n), where s : Spin(n) -> SO(n) is the two-fold covering homomorphism. ...[ and where e_i (x) = SUM(1 to n) gamma^ij (x) e_i so that
e_j(x) e_k(x) + e_k(x) e_j(x) = - 2 g^jk(x) where gamma is the square root of g ]...
... the passage from R and C to more general Clifford algebras allows the notion of fractional linear transformations on R and C to be defined naturally on higher-dimensional Euclidean space. This in turn is used ... to give ... representation theory for Spino(n,1) in parallel with the well-known description of the unitary representations of SL(2,R), thinking of SL(2,R) as a transformation group on C. We derive in the process explicit realizations of the Dirac operator on hyperbolic and spherical space. ...
... The Dirac operator on ... real n-dimensional hyperbolic space Hn ... is defined ... as a differential operator on [ C(infinity) ( Rn+ with coordinates , h ) ]... by
D = ( SUM(1 to n-1) e_i ( y (d/dxi) + (1/2) dt( e_i e_n ) ) + e_n y (d/dy ) ...[where d denotes partial derivative]...
the multiplicative structure on ...[ Cl(n) describes ]... the isometry group of Hn by the action of Spin(n,1) as 'fractional linear tranformations' on Rn+ ...
... The Dirac operator on ... real n-dimensional spherical space Sn ... is defined ... as a differential operator on ...[ C(infinity) ( Rn u {infinity} , h ) ]... by
D = ( 1 + |x|^2 ) ( SUM(1 to n) e_i ( d/dxi) + (1/(1+|x|^2)) dt( e_i x ) ) ) ...[where d denotes partial derivative]...
... the fundamental Bochner-Weizenboeck theorem expresses (-D^2) in general as a second-order Laplacian together with a zero-order curvature operator. ...".
R. S. Krausshar and John Ryan, in math.AP/0212086, Some Conformally Flat Spin Manifolds, Dirac Operators and Automorphic Forms, say:
"... In this paper we study Clifford and harmonic analysis on some conformal flat spin manifolds.... manifolds treated here include RPn and S1 x S(n-1). Special kinds of Clifford-analytic automorphic forms associated to the different choices of are used to construct Cauchy kernels, Cauchy Integral formulas, Green's kernels and formulas together with Hardy spaces and Plemelj projection operators for Lp spaces of hypersurfaces lying in these manifolds. ...... Solutions to the Dirac equation are called Clifford holomorphic functions or monogenic functions. Such functions are covariant under Mobius transformations acting over Rn u {oo} . In fact this covariance is an automorphic invariance best described by a method using Clifford algebras and due to Ahlfors and Vahlen. In fact all solutions to the equation D^k f = 0 where k is in N exhibit a similar automorphic invariance under Mobius transformations. Given this natural method for describing conformal or Mobiustransformations and the automorphic invariance of solutions to D^k f = 0 under actions of the Mobius group a natural choice of generalization of Riemann surfaces from one complex variable to the present context would be conformally flat manifolds. ... Conformally flat manifolds are manifolds with atlases whose transition functions are Mobius transformations. ... one fruitful way of constructing conformally flat manifolds is to factor out a simply connected subdomain U of either the sphere Sn or Rn by a Kleinian subgroup G of the Mobius group where G acts discontinuously on U. This gives rise to the conformally flat manifold U / G. Examples of such manifolds include for example n-tori, cylinders, real projective space and S1 x S(n-1). ...".
Goeffrey Dixon has written Division Algebras: Octonions, Quaternions, Complex Numbers, and the Algebraic Design of Physics (Kluwer 1994), in which he describes Division Algebras and Clifford Algebras. He discusses in some detail how the tensor product RxR = R and CxC = C+C, but QxQ is M(4,R), the matrix algebra of 4x4 matrices of Real Numbers. He shows how Left-Multiplication of Quaternions is distinct from Right-Multiplication, so that the action QL of Left-Multiplication is not identical with the action QR of Right-Multiplication. He also shows:
For more about Clifford algebras, particularly with respect to Cl(0,8), see Why not SEDENIONS? and From Sets to Quarks, particularly Chapter 2. All Lie algebras can be built from Clifford Algebras. Also, it is conjectured that MetaClifford Algebras might be useful.
REFERENCES: Three books that are good places to start reading about the details of Clifford algebras and Spinors are: Clifford Algebras and Spinors, by Pertti Lounesto (London Mathematical Society Lecture Note Series, No 239) Spinors and Calibrations, by F. Reese Harvey, Academic Press (1990). Clifford Algebras and the Classical Groups, by Ian Porteous, Cambridge University Press (1995). Errors can creep into published books and papers in any field. So that errors don't propagate and become widely-held misconceptions, it is important to find them and point them out. The best person I know at doing that is Pertti Lounesto, who has a web page of counterexamples that not only points out errors, but shows why they were probably made, so that the error-correction process not only corrects, but also gives deeper insight into the fundamental structures that led the original authors astray. It is important that authors not be condemned for making errors, so long as they are willing to acknowledge them and correct them. OY! Barry Simon has written YABOGR! The official title is: Representations of Finite and Compact Groups (AMS 1996) What is YABOGR? Read the Book! What does YABOGR do? It, together with ideas of Onar Aam and Ben Goertzel about XOR and set theory, inspires me to write THIS PAGE ABOUT SETS, CLIFFORD GROUPS AND ALGEBRAS, AND THE McKAY CORRESPONDENCE. (any errors you see are due to me, not to Barry Simon, Onar Aam, or Ben Goertzel)
Tony Smith's Home Page ......