Tony's Home 240 Thoughts
Correlations and Lie Sphere Geometry,
historical/cultural studies such as the Kabbala,
mental phenomena such as Archetypes, and
physical phenomena of
| Gravity | Vacuum | BEC | Sonoluminescence | Water Structure |
| Atomic Clusters | Cells and Chips | Qi Field | DNA and Genetic Code |
| Quantum Computing and Superluminal Information | Communication |
of a World in the Many-Worlds is approximated by the 27-dimensional MACROSPACE is the space of 3x3 Hermitian matrices with 3 Octonion spaces O4 , O5, and O6, forming the Jordan algebra J3(O) with the symmetric product AB = (1/2)(AB + BA),
Re(O1) O4 O5
O4* Re(O2) O6
O5* O6* Re(O3)
One 8-dimensional set of neighbors differs from the Given World only by an element of the Octonion space O5.
If it differs only with respect to the timelike real axis plus spacelike associative 3-space of the 8 dimensions of O5, it differs with respect to 4-dimensional PHYSICAL SPACETIME, whose geometry is related to Gravity.
If it differs only with respect to the coassociative 4-space of the 8 dimensions of O5, it differs with respect to 4-dimensional Internal Symmetry MICROSPACE, related to the configuration of the Gauge Bosons of the Color Force, the Weak Force, and Electromagnetism.
A second 8-dimensional set of neighbors differs from the Given World only with respect to an element of the Octonion space O4. It differs with respect to the configuration of Fermion Particles.
A third 8-dimensional set of neighbors differs from the Given World only with respect to an element of the Octonion space O6. It differs with respect to the configuration of Fermion AntiParticles.
The other three 1-dimensional sets of neighbors differing only with respect to the Real Parts of Octonions Re(O1), Re(O2), and Re(O3) do not differ with respect to the configurations of spacetime, gauge bosons, or fermions, but only with respect to the way they interact in the 27-dimensional Jordan algebra J3(O). In other words, these neighbors are identical with respect to the 24-dimensional Chevalley subalgebra of J3(O), but not identical with respect to the full Jordan algebra J3(O).
a Particle-AntiParticle pair (say, Electron E and Positron P) created at a single point of lattice Physicial Spacetime:
EP
The properties of E and P are Correlated because E and P are mirror images of each other with respect to physical properties like electric charge and spin orientation.
As time goes on (up in the illustration), E may move in one direction and P in another direction. At the first time step, E and P will no longer be at the same point, but will be Nearest Neighbors.
E P \ / EP
As time goes on, E and P may become widely separated by many intervening points in lattice Spacetime:
E P \ / \ / \ / \ / EP
If E and P do not interact with other particles during their journey apart, they remain COMPLETELY CORRELATED - the physical properties of E and P remain MIRROR IMAGES of each other.
Even if they undergo interactions changing some of their properties, other properties may remain Correlated.
In any of the spaces of physics, what is
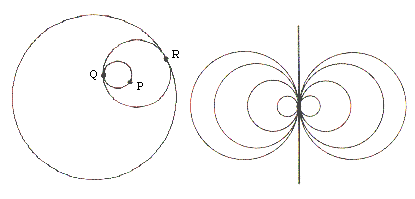
Start with the future light-cone Nearest Neighbors, each and all of them denoted by X, of a point denoted by * at an event that we will take to be the origin event of the Sphere X
X X \ / *
In the continuum approximation of N-dimensional spacetime, they form a Sphere, also denoted by X, that is the intersection of the (N-1)-dimensional future lightcone with an (N-1)-dimensional spacelike hyperplane, so that the dimension of the Sphere X is N-2.
As time goes on toward the future, the Sphere X expands as it gets more distant in time from the point * of origin.
X X \ / \ / \ / *
If another event happens at a point o of the Sphere X, that event can be considered to be the origin event of another Sphere Y
X Y YX \ \ / \ \ / \ o \ / \ / \ / *
Sphere Y is a smaller sphere nested within Sphere X, and tangent to it at point YX, which is so designated because it belongs to both Sphere Y and Sphere X. Since the Sphere Y is inside the Sphere X, the geometry is that of oriented spheres, with the sphere of opposite orientation to Sphere Y being tangent at the same point YX and of the same radius as Sphere Y, but outside Sphere X.
The lightcones originating at * and at o are also nested, and are tangent to each other on the lightlike line from the point o to the point YX.
of the Conformal Group of N-dimensional spacetime. A good introductory paper is Conformal Theories, Curved Phase Spaces Relativistic Wavelets and the Geometry of Complex Domains, by R. Coquereaux and A. Jadczyk, Reviews in Mathematical Physics, Volume 2, No 1 (1990) 1-44, which can be downloaded from the web as a 1.98 MB pdf file. Lie Sphere Geometry is, as described by Amassa Fauntleroy in his papers Projective Ranks of Hermitian Symmetric Spaces, Mathematical Intelligencer 15 (no. 2, 1993) 27-32 and On the Projective Rank of Compact Hermitian Symmetric Spaces, North Carolina State Math preprint 1993, bilholomorphic to the Hermitian Symmetric Space of Lie group cosets
If N = 4, we have Spin(6) / (Spin(4)xSpin(2)) = SU(4) / (SU(2)xSU(2)xU(1)), which is biholomorphic to the Klein quadric Q4 in CP^5. As described by S. G. Gindikin (The Complex Universe of Roger Penrose, Mathematical Intelligencer 5 (no. 1, 1983) 27-35), each point of the 4-complex-dimensional Klein quadric corresponds to a line in CP^3. The line in CP^3 is such that, if it passes through z, it also passes through z* (here * denotes complex conjugate). Through each point z of CP^3, there is one and only one line also passing through z*. Therefore, all of CP^3 is the union of such non-intersecting lines, and CP^3 is fibred into a base manifold M and fibres which are the 1-complex-dimensional lines. The dimension of M is the 3 complex dimensions of CP^3 less the 1 complex dimension of each line, so that M is 2-complex-dimensional, or 4-real-dimensional. All this is fundamental for the theory of Penrose Twistors, in which the Klein quadric Q4 is complexified compactified spacetime, and is related to the isomorphism between Hermitian Symmetric Spaces of types BDI(4) and AIII(2,2) due to
Penrose and Rindler (Spinors and space-time, vol. 1, Cambridge 1984, 1986, section 5.12) show how to describe massive, as well as massless, fields in terms of the lightcone structures of Lie Sphere Geometry.
Tittel, Brendel, Gisin, Herzog, Zbinden, and Gisin, have reported on their Experimental demonstration of quantum-correlations over more than 10 kilometers in quant-ph/9707042.
As Widom, Srivastava, and Sassaroli describe in their paper Acuasal Behavior in Quantum Electrodynamics, quant-ph/9802056, "... conventional quantum electrodynamics allows for interactions to proceed forward and backward in time as well as space-like in direction."
Timelike trajectories can be described by a series of lightcone segments with changes in direction,
\ \ / / *
and spacelike trajectories can be described by a series of lightcone segments, some of which go backward in time (as in the Stueckelberg-Feynman description of antiparticles as particles propagating backward in time).
/\ / \ *
In their paper, Widom, Srivastava, and Sassaroli discuss "... engineering problems involved in experimentally testing such causality violations on a macroscopic scale ..." Their examples include:
sending a superluminal signal, with only a few electrons so that the decay exponent is less than or equal to 1, down a 50 Ohm cable; and
an experiment with two photon coherent sources which are guaranteed to fire off exactly two photons at a time so that the counting statistics at counter 1 depends on how one sets the position of counter 2, via counter 2 events that are possibly space-like or possibly in the future of counter 1 events.
Jack Sarfatti has long advocated studying acausal phenomena in terms of the Bohm formulation of Quantum Theory.
Bohm and Hiley (The Undivided Universe, Routledge 1993, section 15.9) describe the Implicate Order of the Bohm formulation in terms of Lie Sphere Geometry as describing trajectories "... as a kind of enfolded geometric structure whose meaning can be seen all at once as a 'chain' of successively contacting spheres. ... The first step in our trajectory is represented by the point of contact P and a sphere of radius r. The corresponding null ray is in the direction of the radius of the sphere at point P. The next null ray will be represented by a larger sphere contacting the first sphere at the point Q. The next null ray will correspond to a still larger sphere contacting the second sphere at yet another point R. This procedure is to be continued indefinitely so that we obtain a complete description of the zigzag trajectory. ... a sphere of infinite radius ... represents a plane wave. ...

In our model, the implication parameter is just the radius of the sphere. ... we could have the radii of spheres decrease for a while and then increase again. ... this corresponds to pair production. ... The Lagrangian is thus, in our approach, a property of the implicate order which holds at any given moment. ... backward tracks in time are replaced by tracks in which the implication parameter is decreasing."
The equivalence of David Bohm's approach to the Many-Worlds approach has been noted by David Deutsch (The Fabric of Reality, Penguin 1997, pp. 93-94), in which he says: "... Bohm's theory is often presented as a single-universe variant of quantum theory. ... Working out what Bohm's invisible wave will do requires the same computations as working out what trillions of shadow photons will do. Some parts of the wave describe us, the observers, detecting and reacting to the photons; other parts of the wave describe other versions of us, reacting to photons in different positions. ... in his theory reality consists of large sets of complex entities, each of which can perceive other entities in its own set, but can only indirectly perceive entities in other sets. These sets of entities are, in other words, parallel universes. ..."
The D4-D5-E6-E7-E8 VoDou Physics model is fundamentally based on the Conformal structure of Lie Sphere Geometry. It not only contains a Conformal Physical Spacetime
but also is based on the Octonionic Conformal structures
(Reference - Encyclopaedia Britannica Online.)
ARCHETYPES in the human mind may help humans understand the relationships among the various levels.
A few Archetypes ( each of which may contain substructures that are also Archetypes ) are:
AT LEVELS BELOW THE PLANCK ENERGY, our genetic code uses the Double Helix

as do the quantum transactions of the D4-D5-E6-E7-E8 VoDou Physics model. Another archetype for D4-D5-E6-E7-E8 VoDou physics is the geometrical structure of a generalized torus whose equator is the 7-sphere S7. It is S7 x S1 , the product of a 7-sphere S7 and a circle S1. It is a generalized torus because it is NOT the 8-dim torus T8, but when projected into lower dimensions it looks like the 2-torus T2 = S1 x S1. Here is a stereo image of the 2-torus, generated by the program 3D-Filmstrip for Macintosh by Richard Palais.
You can see the stereo with red-green or red-cyan 3D glasses. The program is on the WWW at http://rsp.math.brandeis.edu/3D-Filmstrip. If the horizontal equatorial S1 is expanded to S7, you have S7 x S1, the octonionic structure used in the D4-D5-E6-E7-E8 VoDou Physics model to describe 8-dimensional spacetime. If the horizontal equatorial S1 is expanded to S3, you have S3 x S1, which can describe our 4-dimensional spacetime. If the vertical S1 is taken to be time, flowing upwards, then our 3-dimensional space evolves as indicated roughly by this (730 k) binhexed QuickTime movie. Played in loop mode, it shows evolution through a large-scale closed timelike loop. Another useful low-energy archetype may be the 24-cell, the 4-dimensional regular polytope shown in this stereo view of a 3-D projection (from C program by Michael Gibbs) The 4th dimension is color-coded by blue = +, green = 0, and red = -.
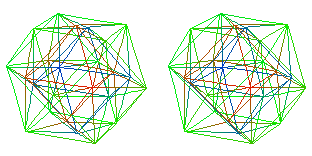
Click here for 742k quicktime.mov animation (It can be played in a loop.) NOTE that this projection of a 24-cell contains a 3-dimensional cuboctahedron
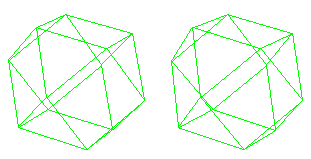
which Fuller called a vector equilibrium and regarded as a fundamental archetype. The 24-cell tiles 4-dimensional space with a tiling that is useful in understanding the Octonion Mirrorhouse. Professor Koji Miyazaki at Kyoto has done much work on such archetypes, including their long history in Asian civilizations. AT THE PLANCK ENERGY LEVEL, useful algebraic structures are Division Algebras such as the octonions and also Clifford Algebras and the sedenions. The 240-vertex Witting polytope is the 8-dimensional counterpart of the 24-cell. The 7-dimensional exotic spheres have as 3-dimensional counterparts the Poincare Dodecahedral Space. Its visualization in terms of platonic solids
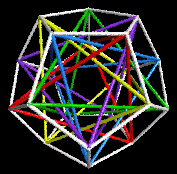
is a useful archetype. It has been illustrated (as above) by Richard Hawkins and by Gerald de Jong, who call it a Mayan Time Star.
The natural fractal structure of octonions has been studied by

Onar Aam and by Girish Joshi. AT LEVELS ABOVE THE PLANCK ENERGY, a useful archetype may be the n-dimensional simplex, the high-dimensional version of the 1, 2, and 3 dimensional line, triangle, and tetrahedron as well as
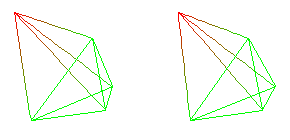
the 4 dimensional pentahedron. WITH RESPECT TO INFORMATION ON ALL LEVELS, a useful archetype may be the 24-dimensional Leech lattice, currently being studied by Geoffrey Dixon, that is related to the extended Golay code G24 and the Monster finite simple group, a group of order 2^46 3^20 5^9 7^6 11^2 13^3 17 19 23 29 31 41 47 59 71, or about 8 x 10^53. The Monster is naturally represented on a space of 196,884 dimensions, which can be broken down into 196,560 + 300 + 24. Since 300 = 25x24/2 is the symmetric square of 24, and since the Leech lattice discrete nearest-neighbor sphere has 196,560 points, and since IF the 196,560 points form a group, just as the 240 of an E8 lattice form unit octonions and as the 24 of a D4 lattice form unit quaternions then it should be possible to form the 196,560 dimensional space of the group algebra of the Leech lattice nearest-neighbor group, and then add the 300-dim space of symmetric squared Leech lattice, and then add the 24-dim space of the Leech lattice itself, to get the 196,884-dim representation space of the Monster. By going down to the underlying 24-dim Leech lattice space, it should be possible to represent the Monster on the 24-dim space of the Leech lattice. Not having a 24-dim or 196,560-dim or 196,884-dim picture, here is a Penrose tiling that is a low-dimensional slice thereof:

Quantum Information Theory is not the same as classical information theory. For example, Calderbank, Rains, Shor, and Sloane have shown that whereas many useful classical-error-correcting codes are binary over the field GF(2), quantum-error-correcting codes are quaternary over the field GF(4). As Dixon has noted, GF(4) is related to quaternions as GF(2) is to complex numbers and GF(8) is to octonions.
UNIVERSAL TRANSFORMATIONS are interpreted by IFA
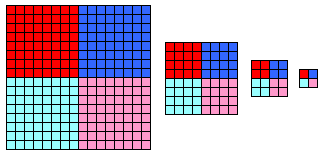
and by the I CHING.
The 4x4x4 = 64 genetic code, the 2x2x2x2x2x2 = 64 I Ching, and the 8x8 = 64 D4-D5-E6-E7 physics model are all just different representations of the same fundamental structure. This fundamental structure is not only shared by Golay codes and Leech lattice but also by Penrose tilings and musical sequences.
| Gravity | Vacuum | BEC | Sonoluminescence | Water Structure |
| Atomic Clusters | Cells and Chips | Qi Field | DNA and Genetic Code |
| Quantum Computing and Superluminal Information | Communication |
| NanoMachines and the Second Law | DARPA |
......