Bound states of fermions should correspond to soliton solutions for the full effective Lagrangian for the fermions in the bound state. Such a soliton solution would include the effects of interactions of the fermions with virtual vacuum gauge bosons and fermion-antifermion pairs, but would be difficult to calculate in general. However, the interpretation of fermion bound states as solitons leads to calculable results in some cases:
Since, by Deser's theorem, there are no solitons for pure SU(n) Yang-Mills theories (without fermion or scalar source terms) for spacetime dimensions other than 4+1, there can be no pure gluon glueballs in the physical 3+1 dimensional spacetime of the effective field theory in the D4-D5-E6 model.
Since neutrinos are coupled only to the weak force, they do not produce easily observable bound states.
Since electrons, muons, and tauons interactions with the weak force and gravitation are too weak to produce easily observable bound states, and the only other force to which they are coupled is the electromagnetic force, their bound states can be approximated by the nonrelativistic quantum theory of Coulomb electromagnetic interactions.
Quark interactions with the weak force and gravitation are too weak to produce easily observable bound states. Quark interactions with the electromagnetic force are much weaker than interactions with the SU(3) color force, so the soliton bound states can be calculated for the SU(3) color force, with the electromagnetic effects to be considered as correction factors.
Such Soliton structures can be described in terms of Compton Radius Vortex structures.
There are two ways a color-neutral soliton can be formed:
a red-blue-green triple of quarks; or
a quark-antiquark pair.
This paper deals with the quark-antiquark pair.

From the point of view of the SU(3) color force, and ignoring the electromagnetic force, the charged pion is the lowest energy bound quark-antiquark pair state, either u_d or _u d . It should be spherically symmetric in space, and therefore representable by a soliton solution in 1+1 dimensions if the 3+1 dimensional solution is of the form (1/r^2)f(r,t) so that the corresponding 1+1 dimensional solution is of the form f(r,t) and if all pertinent operators are similarly transformed.
Sine-Gordon Breathers are described on the web in the Soliton-Lab Art Gallery in Kyoto in which there is a Permanent Exhibition of the Many Faces of Solitons. in which there is a Sine-Gordon equation page. They are also described by Sidney Coleman in his Erica lecture paper Classical Lumps and their Quantum Descendants (1975), reprinted in his book Aspects of Symmetry (Cambridge 1985); and by R. Rajaraman in his book Solitons and Instantons (North-Holland 1982,1987).
Marin, Eilbeck, and Russell, in their paper Localized Moving Breathers in a 2-D Hexagonal Lattice, show "...that highly localized in-plane breathers can propagate in specific directions with minimal lateral spreading ... This one-dimensional behavior in a two-dimensional lattice was called quasi-one-dimensional (QOD) ..." (In their paper, dimensionality refers to spatial dimensionality.) They use QOD behavior to describe phenomena in muscovite mica crytstals. The Sine-Gordon Breather model of the pion in the D4-D5-E6 model uses similar QOD behavior to describe the pion.
If the quark is taken to correspond to a soliton and the antiquark to an antisoliton, the natural representation is by a doublet or breather solution to the sine-Gordon equation
L = (1/2)(df)^2 - mo^2(m^2/j)(cos(sqrt j /m)f - 1).
At the classical level, the sine-Gordon Lagrangian can be scaled to be independent of the parameter j /m^2, but the quantum energy levels depend on j /m^2 as is discussed by Rajaraman.
According to Rajaraman, classical solutions to the sine-Gordon equation include:
the soliton f(mx) = 4(m / sqrt j) arctan(exp(mx));
the antisoliton f(mx) = - 4(m / sqrt j) arctan(exp(mx)) = -f(mx); and
the doublet, or Breather
fv(mx,mt) = 4(m / sqrt j) arctan(sin(vmt / sqrt (1+v^2))/vcosh(mx / sqrt (1+v^2))).

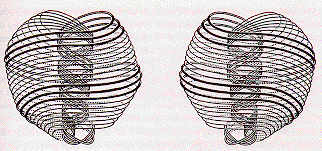
The doublet breather is confined in space (y-axis) but periodic in time (x-axis). This stereo image of a doublet breather was generated by the program 3D-Filmstrip for Macintosh by Richard Palais. You can see the stereo with red-green or red-cyan 3D glasses. The program is on the WWW at http://rsp.math.brandeis.edu/3D-Filmstrip. Here is another parameterized view of the doublet breather:

In the doublet, v is a parameter related to Lorentz-transforming the solution away from its rest frame. The doublet is a periodic solution with period 2pi sqrt (1+v^2)/v , and can be thought of as a bound soliton-antisoliton pair oscillating with respect to each other.
In the doublet's rest frame, its field is confined within the envelope
±4 (m / sqrt j) arctan( (1/v) sech(mx / sqrt (1+v^2)) ) .
If Msol is taken to be the mass of the soliton (or antisoliton) that is oscillating with respect to the antisoliton (or soliton), and if m is taken to be the mass of the doublet bound state, called the meson mass, then in the quantum theory, to leading order, Msol = 8m^3/ j - m /pi , where the term 8m^3/ j is the classical mass and the term -m /pi is the leading order quantum correction.
Assuming that the quantum correction term should also be of the form m^3/ j , the leading order formula for Msol requires that j/m^2 = pi. In that case, Msol = (8m - m)/pi = (7/pi) m.
Then, if Msol is interpreted as the constituent mass of a first-generation quark or antiquark and m as the pion mass, the D4-D5-E6 model gives
m(pion) = (pi/7) Msol(quark) = 312.75pi/7 = 140.4 Mev.
Experimentally, m(pion) = 139.57 Mev, which is in pretty good agreement with the D4-D5-E6 model leading order calculation.
A near-coincidence between the electromagnetic fine structure constant (about 1/137) and the positronium (electron-positron bound state) / pion mass ratio (about 1/135) has been noticed in the context of some physics models (including but not necessarily limited to that of Ernest J. Sternglass). In the context of the D4-D5-E6-E7-E8 VoDou Physics model, I have the following view of the physics of that near-coincidence:
e --- p separated, distinct pair sum of masses = 0.5 + 0.5 = 1.0 MeV exchange virtual bosons (photons) with probability 1/137 u --- ubar separated, distinct pair sum of constituent masses = 612 + 612 = 1224 MeV exchange virtual bosons (gluons) with probability 0.6 u ubar merged as sine-Gordon doublet breather pion merge until they exchange virtual bosons (gluons) with probability 1 since probability 1 (for merged pion) is 137 times probability 1/137 (for positronium) at full pion level of merger, pion mass is about 137 x e-p = 137 MeV
For the sine-Gordon doublet, an approach similar to the WKB formula for the hydrogen atom, called by Coleman the DHN formula for its originators Dashen, Hasslacher, and Neveu, may be an exact formula for the doublet energy levels.
Assuming that j /m^2 = pi, the DHN formula gives
m(pion) = 2 Msol(quark) sin((j/m^2)/16(1-(j /m^2)/8pi)) = = 2 Msol(quark) sin(pi/14).
Then, since in the D4-D5-E6 model Msol(quark) = 312.8 Mev, m(pion) = 625.6 sin(pi/14) = 139.2 Mev.
That is closer to the experimental value m(pion) = 139.57 Mev.
Sine-Gordon and Massive Thirring equations: In section 7.3, Rajaraman, uses the approach of Mandelstam to start with the sine-Gordon operator f to construct the operator P of the massive Thirring equation
L = iP d P - mF PP - (1/2)g(PP ) (PP ),
where mo^2(m^2/ j)cos((sqrt j/m)f) = - mFPP ,
j/4pi m^2 = 1/(1 + g/pi), and
-(sqrt j/2pi m) e(mnop) f = PP .
As discussed by Coleman as well as Rajaraman, the massive Thirring model in P describes a massive fermion-antifermion pair in one space dimension and is equivalent to the sine-Gordon equation in f.
Given f , the two-component Fermi field P in 1+1 dimensions is defined by P1(x) = C1 exp(A1(x)) and P2(x) = C2 exp(A2(x)) , where
A1(x) = (-2 pi i m / sqrt j)(Int[-oo,x] f(x') - (i sqrt j / 2m) f(x)
A2(x) = (-2 pi i m / sqrt j)(Int[-oo,x] f(x') + (i sqrt j / 2m) f(x)
Then there is the commutation relation
[f(y),y(x)] = (2pi m / sqrt j) q(x-y) y(x) , where q(x-y) is the step function.
The operator y(x) raises the value of the field j by 2ım / ÷l to the left of x and leaves it unchanged to the right of x.
The operator y(x) reduces the soliton state [f(oo) - f(-oo)] = 2ım / ÷l to the vacuum state [j(oo) - j(-oo)] = 0 .
If, according to the main assumption of this section, j/m^2 = pi, then the soliton state f(oo) = - f(-oo) = sqrt pi ,
For j/m^2 = pi the first coefficient of A1 and A2 is -i2 sqrt pi and the second coefficient is ±(i sqrt pi)/2 . Then A1(oo) - A2(oo) = -i pi.
WHAT ABOUT THE NEUTRAL PION? The quark content of the charged pion is u_d or d_u , both of which are consistent with the sine-Gordon picture. Experimentally, its mass is 139.57 Mev. The neutral pion has quark content (u_u + d_d)/sqrt(2) with two components, somewhat different from the sine-Gordon picture, and a mass of 134.96 Mev. The effective constituent mass of a down valence quark increases (by swapping places with a strange sea quark) by about DcMdquark = (Ms - Md) (Md/Ms)2 aw V12 = = 312x0.25x0.253x0.22 Mev = 4.3 Mev. Similarly, the up quark color force mass increase is about DcMuquark = (Mc - Mu) (Mu/Mc)2 aw V12 = = 1777x0.022x0.253x0.22 Mev = 2.2 Mev. The color force increase for the charged pion DcMpion± = 6.5 Mev. Since the mass Mpion± = 139.57 Mev is calculated from a color force sine-Gordon soliton state, the mass 139.57 Mev already takes DcMpion± into account. For pion0 = (u_u + d_d)/ sqrt 2 , the d and _d of the the d_d pair do not swap places with strange sea quarks very often because it is energetically preferential for them both to become a u_u pair. Therefore, from the point of view of calculating DcMpion0, the pion0 should be considered to be only u_u , and DcMpion0 = 2.2+2.2 = 4.4 Mev. If, as in the nucleon, DeM(pion0-pion±) = -1 Mev, the theoretical estimate is DM(pion0-pion±) = DcM(pion0-pion±) + DeM(pion0-pion±) = = 4.4 - 6.5 -1 = -3.1 Mev, roughly consistent with the experimental value of -4.6 Mev.
WHAT ABOUT SU(3)xSU(3) CHIRAL THEORY OF SPIN-0 MESONS? To see how chiral theory might be useful, define the relationship between the calculated constituent quark masses, denoted by mq, and QCD Lagrangian current quark masses, denoted by Mq, by Mq = mq - mu = mq - md = mq - 312.8 MeV. This makes, for the QCD Lagrangian, the up and down quarks roughly massless. Therefore the current masses can be used as input for the SU(3)xSU(3) chiral theory that, although it is only approximate because the constituent mass of the strange quark is about 312 MeV, rather than nearly zero, can be useful. SU(3)xSU(3) chiral theory can be used to get a rough estimate of the pion mass, and other meson masses. While I think that SU(3)xSU(3) chiral theory is not as accurate as the sine-Gordon soliton approach for mesons, the SU(3)xSU(3) chiral theory is more conventional, more highly developed, and more widely understood, so I will describe it here: To get the pion mass by the SU(3)xSU(3) chiral theory, recall that the 3 quarks of the SU(3) are the up quark and down quark, with roughly zero current mass for Mu and Md, and the strange quark, for which the calculated constituent mass ms = 625 MeV, so that the current Ms = ms - 313 = 312 MeV. This is somewhat higher than the 100 to 200 MeV usually used for the current strange mass Ms, but I will it for SU(3)xSU(3) chiral theory to get the Gell-Mann-Okubo relation 3 eta^2 + pion^2 = 4 kaon^2 (where eta, pion, and kaon denote masses of those mesons) Then assume: 1 - there are two types of spin-0 mesons, pion-type, made up of a quark-antiquark pair that "virtually cancel each other out part of the time", with maximal cancellation for the pion made of up and down quarks, so that for pion-type mesons the total mass is the pion mass plus the current masses (or excess of constituent mass over up or down) of any quarks other than up or down (in the chiral theory, the pion mass is considered unknown until it is calculated using the Gell-Mann-Okubo formula); and eta-type, made up of a quark-antiquark pair that do not "virtually cancel each other out part of the time" but "float together on a pion-type sea" so that meson mass is the sum of the constituent masses of the quark and anti-quark less the pion mass; 2 - the kaon is pion-type, in fact just like a pion except that one of the quark-antiquark pair is strange rather than down, so the kaon mass is the pion mass plus the excess of the strange constituent mass over the down constitutent mass, or, from another point of view, the current mass of the strange quark, so that kaon = pion + 312 MeV; 3 - the eta is eta-type, so that the eta mass is twice the up or down quark constituent mass, less the pion mass because the quark and antiquark "float in a pion sea" so that eta = 2 x 313 - pion = 626 MeV - pion. Then, from Gell-Mann-Okubo: 3 eta^2 + pion^2 = 4 kaon^2 3(391,876 - 1248 pion + pion^2) + pion^2 = = 4(97,344 + 624 pion + pion^2) 3(391,876 - 1248 pion + pion^2) + pion^2 = = 4(97,344 + 624 pion + pion^2) 1,175,628 - 3,744 pion + 3 pion^2 + pion^2 = = 389,376 + 2,496 pion + 4 pion^2 786,252 MeV = 6,240 pion pion = 126 MeV kaon = 126 + 312 MeV = 438 MeV eta = 626 - 126 MeV = 500 MeV Experimentally, the results are: pion = 134 MeV (for neutral pion) kaon = 497 MeV (for neutral kaon) eta = 547 MeV If continue, you can exhaust the possibilities of up-down-strange quarks combined in pion-type or eta-type ways, to make: eta' as pion-type with two strange parts, for mass eta' = pion + 312 + 312 MeV = 750 MeV (experimentally eta' = 958 MeV) eta(1295) as eta-type with one strange part, for mass eta(1295) = 625 + 313 - pion = 812 MeV (experimentally eta(1295) = 1,295 MeV) eta(1440) as eta-type with two strange parts, for mass eta(1440) = 625 + 625 - pion = 1,124 MeV (experimentally eta(1440) = 1,440 MeV)
CHARGED AND NEUTRAL KAONS: Just as there is a mass difference between charged and neutral pions, there is also a mass difference between charged and neutral kaons: K0 mesons, quark content (s_d or _sd), have mass about 497.7 Mev, and K± mesons (s_u or _su) have mass about 493.6 Mev, which is somewhat greater than the sum of the pion mass (=135 Mev) and the excess of the strange quark mass over the u-d quark mass (=313 Mev). In the K0, the effective constituent mass of a down valence quark increases (by swapping places with a strange sea quark) by about (Ms - Md) (Md/Ms)2 aw V12 = 312x0.25x0.253x0.22 Mev = 4.3 Mev. If the strange quark swaps places with a down sea quark, it just gives the down sea quark "kinetic" energy in the amount of the mass excess of a strange quark over a down quark, so the effective constituent mass of the strange quark is unchanged, and DcMK0 = 4.3 Mev. However, in the K±, the up quark color force mass increase is (Mc - Mu) (Mu/Mc)2 aw V12 = 1777x0.022x0.253x0.22 Mev = 2.2 Mev, so DcM(K0-K±) = 4.3 - 2.2 = 2.1 Mev. If DeM(K0-K±) = -1 Mev, then DM(K0-K±) = -1 + 2.1 = 1.1 Mev, roughly consistent with the experimental value of 4.1 Mev.
WHAT ABOUT SPIN-1 MESONS? The rho vector mesons have the same quark content as pions, but have parallel spins, and so are spin-1 instead of spin-0. Therefore they do not form sine-Gordon doublet type solitons. The rho mass, about 770 Mev, is approximately the sum of the constituent masses of an up quark and a down antiquark plus the mass of a pion binding them (312.75 + 312.75 + 139.187 = 764.687 Mev).
WHAT ABOUT MESONS MADE OF HEAVY QUARKS? For mesons made up of quarks substantially more massive than the up and down quarks of the pion, the sine-Gordon soliton picture and the chiral Lagrangian picture are relatively less important than the constituent quark picture in which the meson mass is roughly the sum of the valence quark constituent masses. D0 mesons, quark content (c_u o _cu), have mass about 1864.5 Mev, and D± mesons (c_d or _cd) have mass about 1869.3 Mev, which is somewhat less than the sum of the pion mass (=135 Mev) and the excess of the charm quark mass over the u-d quark mass (=1,770 Mev). In the D±, the effective constituent mass of a down valence quark increases by about 4.3 Mev. If the charm quark swaps places with an up sea quark, it just gives the up sea quark "kinetic" energy in the amount of the mass excess of a charm quark over a up quark, so the effective constituent mass of the charm quark is unchanged, and DcMD± = 4.3 Mev. However, in the D0, the up quark color force mass increase is about 2.2 Mev, so DcM(D0-D±) = 2.2 - 4.3 = -2.1 Mev. If DeM(D0-D±) = -1 Mev, then DM(D0-D±) = -1 - 2.1 = -3.1 Mev, roughly consistent with the experimental value of -4.8 Mev. Ds mesons, quark content (c,s), have mass about 1,970 Mev, which is somewhat less than the sum of the charm quark mass (2,085 Mev) and the strange quark mass (625 Mev). etac mesons, quark content (c,_c), have mass about 2,980 Mev, which is somewhat less than twice the charm quark mass (4,170 Mev). upsilon mesons, quark content (b,`b), have mass about 9,460 Mev, which is somewhat less than twice the beauty quark mass (11,260 Mev). B0 mesons, quark content (b_d or _bd), have mass about 5279.4 Mev, and B± mesons (b_u or _bu)have mass about 5277.6 Mev, which is somewhat less than the sum of the pion mass (135 Mev) and the excess of the beauty quark mass over the u-d quark mass (5,317 Mev). In the B0, the effective constituent mass of a down valence quark increases by about 4.3 Mev. If the beauty quark swaps places with an down or strange sea quark, it just gives the down or strange sea quark "kinetic" energy in the amount of the mass excess of a beauty quark over a down or strange quark, so the effective constituent mass of the beauty quark is unchanged, and DcMB0 = 4.3 Mev. However, in the B±, the up quark color force mass increase is about 2.2 Mev, so DcM(B0-B±) = 4.3 - 2.2 = 2.1 Mev. If DeM(B0-B±)= -1 Mev, then DM(B0-B±) = -1 + 2.1 = 1.1 Mev, roughly consistent with the experimental value of 1.8 Mev.
......