Tony Smith's Home Page

From Sets to Quarks:

Deriving the Standard Model plus Gravitation 
from Simple Operations on Finite Sets
by Tony Smith
 
is a 1997 paper (hep-ph/9708379) 
describing a TOE:  
the HyperDiamond Feynman Checkerboard model of physics. 

According to John C. Baez and S. Jay Olson in their paper at gr-qc/0201030:

"... Ng and van Dam have argued that quantum theory and general relativity give a lower bound delta L > L^(1/3) L_P ^(2/3) on the uncertainty of any distance, where L is the distance to be measured and L_P is the Planck length. Their idea is roughly that to minimize the position uncertainty of a freely falling measuring device one must increase its mass, but if its mass becomes too large it will collapse to form a black hole. ... Amelino-Camelia has gone even further, arguing that delta L > L^(1/2) L_P ^(1/2) ... Here we show that one can go below the Ng-van Dam bound [ and the Amelino-Camelia bound ] by attaching the measuring device to a massive elastic rod. ...

[ while the Ng-van Dam ] result was obtained by multiplying two independent lower bounds on delta L, one from quantum mechanics and the other from general relativity, ours arises from an interplay between competing effects. On the one hand, we wish to make the rod as heavy as possible to minimize the quantum-mechanical spreading of its center of mass. To prevent it from becoming a black hole, we must also make it very long. On the other hand, as it becomes longer, the zero-point fluctuations of its ends increase, due to the relativistic limitations on its rigidity. We achieve the best result by making the rod just a bit longer than its own Schwarzschild radius.

... Relativistic limitations on the rod's rigidity, together with the constraint that its length exceeds its Schwarzschild radius, imply that zero-point fluctuations of the rod give an uncertainty delta L > L_P . ...".

Since the D4-D5-E6-E7-E8 VoDou Physics model is 
fundamentally a Planck Scale HyperDiamond Lattice 
Generalized Feynman Checkerboard model, 
it violates Lorentz Invariance at the Planck Scale, 
affecting Ultra High Energy Cosmic Rays. 

ABSTRACT:
 
From sets and simple operations on sets, 
a Feynman Checkerboard physics model is constructed 
that allows computation of force strength constants and 
constituent mass ratios of elementary particles, 
 
with a Lagrangian structure that gives a Higgs scalar
particle mass of about 146 GeV and a Higgs scalar
field vacuum expectation value of about 252 GeV, 
 
giving a tree level constituent Truth Quark ( top quark ) mass 
of roughly 130 GeV, which is (in my opinion) supported 
by dileptonic events and some semileptonic events. 
See 
http://www.innerx.net/personal/tsmith/TCZ.html 
 
Table of Contents: 
Chapter 1 - Introduction. 
Chapter 2 - From Sets to Clifford Algebras. 
 
                 MANY-WORLDS QUANTUM THEORY.  
 
Chapter 3 - Octonions and E8 lattices. 
Chapter 4 - E8 spacetime and particles. 
Chapter 5 - HyperDiamond Lattices. 
Chapter 6 - Spacetime and Internal Symmetry Space. 
Chapter 7 - Feynman Checkerboards. 
Chapter 8 - Charge = Amplitude to Emit Gauge Boson. 
Chapter 9 - Mass = Amplitude to Change Direction. 
Chapter 10 - Protons, Pions, and Physical Gravitons. 
Appendix A - Errata for Earlier Papers. 
References.

The HyperDiamond Feynman Checkerboard model 
is a discrete model similar to 
the continuum structures of the D4-D5-E6-E7-E8 VoDou Physics model. 
Its natural Clifford algebra structure 
produces a Many-Worlds Quantum Theory. 
 
The model describes:

• Our 4-dimensional Physical SpaceTime;
• 4-dimensional Internal Symmetry Space;
• SU(3)xSU(2)xU(1) Gauge Bosons, Gravity, the Higgs Mechanism, and Complex Propagator Phase;
• 3 Generations of Musaka/Ganesha Fundamental Elementary Fermion Particles.

The Musaka/Ganesha Particles are NOT the Gaja/Ganesha Physical Electrons, Neutrinos, and Quarks, but are the Musaka/Ganesha Virtual Sea and Valence Particles in the Gaja/Ganesha Compton Vortices that are the Physical Electrons, Neutrinos, and Quarks. The Ganesha terminology is based on works of Sidharth, who described Physical Elementary Particles as Compton Vortices.

The structural basis of the HyperDiamond Feynman Checkerboard model 
is the 4-dimensional Hyperdiamond lattice. 

The Discrete HyperDiamond Generalized Feynman Checkerboard and Continuous Manifolds are related by Quantum Superposition:

• Elements of a Discrete Clifford algebra correspond to Basis Elements of a Real Clifford algebra.
• General Elements of a Real Clifford algebra correspond to Superpositions of Basis Elements = Elements of the underlying Discrete Clifford algebra.
  • Volumes of Spaces of Superpositions of some given Sets of Basis Elements correspond to Mass or Charge of Particles or Forces represented by those Basis Elements.
  • Volumes of Spaces of Superpositions of other given Sets of Basis Elements correspond to Volume of Physical SpaceTime and Volume of Internal Symmetry Space represented by those Basis Elements.

The HyperDiamond Feynman Checkerboard model makes these tree level (quark masses are constituent masses) predictions of particle masses and charges, with charges being given by their squares, the force strength constants.

Particle Masses are calculated by using:

• ratios of volumes of bounded complex homogeneous domains and their Shilov boundaries; and
• combinatiorial relationships.

Force Strengths are calculated by using:

• ratios of volumes of bounded complex homogeneous domains and their Shilov boundaries; and
• mass factors for the weak force and gravity, which mass factors have a visualization (arising from e-mail discussion with Dick Andersen): Gauge bosons are visualized as going from a source through a medium to a target:
  • The weak force mass factor is related to the Higgs mechanism. The Higgs scalar field absorbs some of the weak bosons as they go through the medium, thus weakening the weak force and producing the weaker effective weak force that is observed by experiments;
  • The graviton by itself is long-range and massless, but virtual Planck-mass black holes in spacetime absorb some of the gravitons as they go through the spacetime medium, thus weakening the gravitational force and producing the weaker effective gravitational force that is observed by experiments;

 

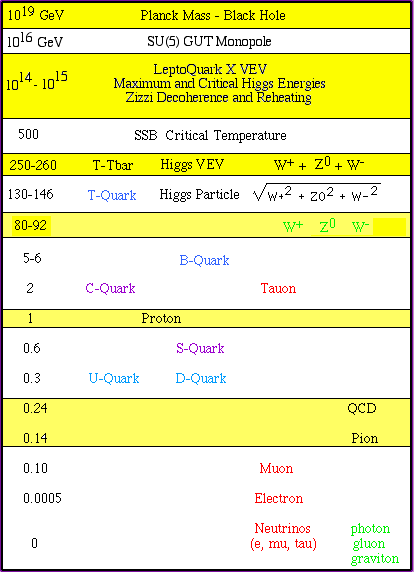
Based on the given electron mass, 
all other particle masses in this diagram 
(the massless gluons are confined, 
the massless Spin(5) gravitons are confined, 
but the massless physical gravitons propagate) 
are calculated in the model:    

Here is how the mass ratios work:

• the electron / Truth quark mass ratio is fixed, as are the mass ratios of all fundamental fermions;
• the Truth - antiTruth quark pair mass corresponds to the sum of the masses of the weak bosons W+, W-, and W0;
• the W0 / Z0 mass ratio is fixed, and the sum of the masses of the weak bosons W+, W-, and Z0 corresponds to the Vacuum Expectation Value of the Higgs scalar field that transforms the W0 into the Z0;
• the Planck mass is a condensation of fermion-antifermion pairs, somewhat like a pion condensate;
• the SU(5) LeptoQuark X-bosons have a Vacuum Expectation Value corresponding to a decoherence / condensate below the Planck mass.

It is interesting that

Based on the geometric part of the gravitational force being unity, the Relative Force Strengths of G (gravity), C (color force), W (weak force) and E (electromagnetism) are calculated from the formulae:

alphaG = (1 / MG^2 ) ( Vol(MISG) )
                     ( Vol(QG) / Vol(DG)^( 1 / mG ))
 
alphaC = alphaS = ( 1 / MC^2 ) 
                  ( Vol(MISC) ) 
                  ( Vol(QC) / Vol(DC)^( 1 / mC ))

alphaW = ( 1 / MW^2 ) 
         ( Vol(MISW))
         ( Vol(QW) / Vol(DW)^( 1 / mW ))
 
alphaE = ( 1 / ME^2 ) 
         ( Vol(MISE) )
         ( Vol(QE) / Vol(DE)^( 1 \/ mE ))

------------------------------------------------------------

alphaG = (1 / MG^2 ) ( Vol(S4) )
                     ( Vol(RP1xS4) / Vol(DG)^( 1 / 4 ))

alphaC = alphaS = ( 1 / 1 ) 
                  ( Vol(CP2) ) 
                  ( Vol(S5) / Vol(B6)^( 1 / 4 ))

alphaW = ( 1 / MW^2 ) 
         ( Vol(S2xS2))
         ( Vol(RP1xS2) / Vol(DW)^( 1 / 2 ))

alphaE = ( 1 / 1 ) 
         ( Vol(T^4) )
         ( Vol(1) / Vol(1)^( 1 \/ 1 ))
 
------------------------------------------------------------

The results of the calculations are: 

electromagnetic fine structure constant = 1/137.03608;
 
weak force Gfermi = (Gweak)(Mproton)^2 = 1.02 x 10^(-5); 
 
color force strength = 0.6286 (at 0.245 GeV);

By using the lowest order renormalization equation  
the running values of the color force strength are: 
color force strength = 0.167 (at 5.3 GeV);
color force strength = 0.121 (at 34 GeV); and
color force strength = 0.106 (at 91 GeV)
Color force strength calculation used Perturbative QCD.
If Nonperturbative QCD and other things are taken into account,
then the color force strength = 0.123 (at 91 GeV)

Based on the geometric part of the gravitational force being unity, 
all other force strengths 
(blue is weak force, red is color force, green is electromagnetism) 
in this diagram 
(horizontal axis is log(10) of energy in Gev) 
are calculated in accord with SU(5) Grand Unification:  
 

  
           

the Higgs field vacuum expectation value is about 252 GeV; 
 

the Truth quark-antiquark t-tbar mass is 259.031 GeV, 
giving a Truth Quark mass of 129.5155 GeV,
usually rounded to 130 GeV; 
 

the sum of the masses of W+, W-, and W0 is 
80.326 + 80.326 + 98.379 = 259.031 GeV, 
usually rounded to 260 GeV; 
 
and  
the sum of the masses of W+, W-, and Z0 is 
80.326 + 80.326 + 91.862 = 252.514 GeV, 
usually rounded to 80 + 80 + 92 = 252 GeV. 
 

the fermion masses are
 
Me = 0.5110 MeV (assumed);
Me-neutrino = Mmu-neutrino = Mtau-neutrino = 0;
Md = Mu = 312.8 MeV (constituent quark mass);
Mmu = 104.8 MeV;
Ms = 625 MeV (constituent quark mass);
Mc = 2.09 GeV (constituent quark mass);
Mtau = 1.88 GeV;
Mb = 5.63 GeV (constituent quark mass);
Mt = 130 GeV (constituent quark mass).
 

Kobayshi-Maskawa parameters come from
quark constituent masses and lepton masses:
 
               d                    s                     b
 
u            0.975               0.222         0.00249 - 0.00388 i
 
c           -0.222               0.974                0.0423
            -0.000161 i         -0.0000365 i
 
t            0.00698            -0.0418               0.999
            -0.00378 i          -0.00086 i
 
 
according to the following formulas:
 
phase angle d13 = 1 radian
sin(a) = [Me+3Mu+3Md] /Sqrt( [Me^2+3Mu^2+3Md^2] + [Mmu^2+3Mc^2+3Ms^2] )
sin(b) = [Me+3Mu+3Md] /Sqrt( [Me^2+3Mu^2+3Md^2] + [Mtau^2+3Mt^2+3Mb^2] )
sin(g') = [Mmu+3Mc+3Ms] /Sqrt( [Mmu^2+3Mc^2+3Ms^2] + [Mtau^2+3Mt^2+3Mb^2] )
sin(g) = sin(g') Sqrt( [Mmu+3Mc+3Ms] / [Me+3Mu+3Md] )
 

Weinberg Angle s2w = 0.235

 
Pions and Protons are 4-D versions of: 
 
Sine-Gordon Breathers made up of quark-antiquark pairs for pions; 
 
and 
 
Nontopological Solitons similar to tHooft-Polyakov monopoles 
made up of rgb quark triples for protons.
 

The Planck mass is the mass of a condensate of pions at one point, 
and 
Gravitational G = (Ggravity)(Mproton)^2 = 5 x 10^(-39);
 

HERE is a 1995 paper on the 4-dim HyperDiamond Feynman Checkerboard.
 

Here is some selected Truth Quark material,
in inverse chronological order.
 

Here is some 1984-1992 history of the Truth Quark.
 

 
The D4-D5-E6-E7 physics model emerges from bits 
just as it does from the points of 
Simplex Physics above the Planck Energy 
which is similar to its emergence 
from the arrows of quantum set theory 
and from the structure of Metaclifford algebras. 
 
 
The mathematical structures used in the D4-D5-E6-E7 model are 
much like the structures of: 
 
IFA              -  Cl(8) Clifford Algebra; 
Wei Qi           -  Spin(8) vector HyperDiamond lattice; 
I Ching          -  Spin(8) bivector gauge bosons; 
Tai Hsuan Ching  -  Spin(8) spinor fermions; 
Tarot            -  E6.    
 

Tony Smith's Home Page

......