Frank Dodd (Tony) Smith, Jr. - November 2007 - www.valdostamuseum.org/hamsmith/
Abstract
Garrett Lisi, in a 6 November 2007 paper 07110770 on the Cornell arXiv in hep-th (as of 16 November 2007), proposed "An Exceptionally Simple Theory of Everything" based on the struucture of the 248-dimensional exceptional Lie algebra E8. This paper compares his geometric structure and physical interpretation with that of my physics model based on the 256-dimensional Cl(8) Clifford algebra. This paper has three sections:
In this paper I am, for simplicity of exposition, often ignoring signature (for example, writing Cl(8) for Cl(1,7), etc).
Garrett Lisi, in a 6 November 2007 paper 07110770 on the Cornell arXiv in hep-th (as of 16 November 2007), said:
"... All fields of the standard model and gravity are unified as an E8 principal bundle connection. ... three generations of fermions [are] related by triality. The interactions and dynamics ... are described by the curvature and action over a four dimensional base manifold. ...
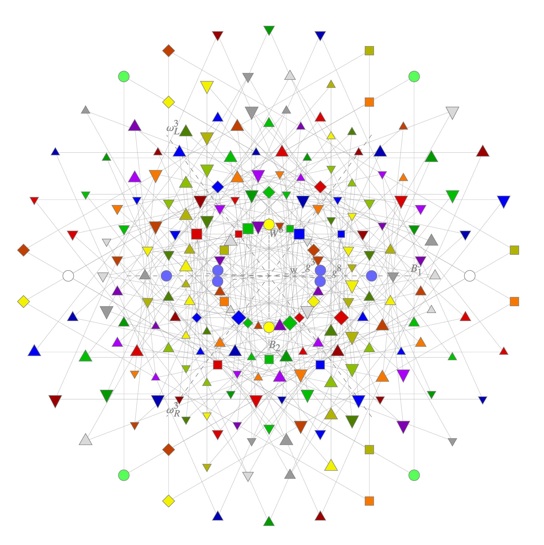
The weights of ... 222 elements - corresponding to the quantum numbers of all gravitational and standard model fields - exactly match 222 roots out of the 240 of the largest simple exceptional Lie group, E8. ... The E8 root system ... with elementary particle symbols assigned to their associated roots according to Table 9, is shown ...with lines drawn between triality partners ...

...[In the] plot...[shown below]... of E8 showing a rotation ...[ I have rotated the image about 150 degrees from Garrett's figure ]...
[ Note that in the above rotated image some of the 240 E8 vertices are projected to the same point:
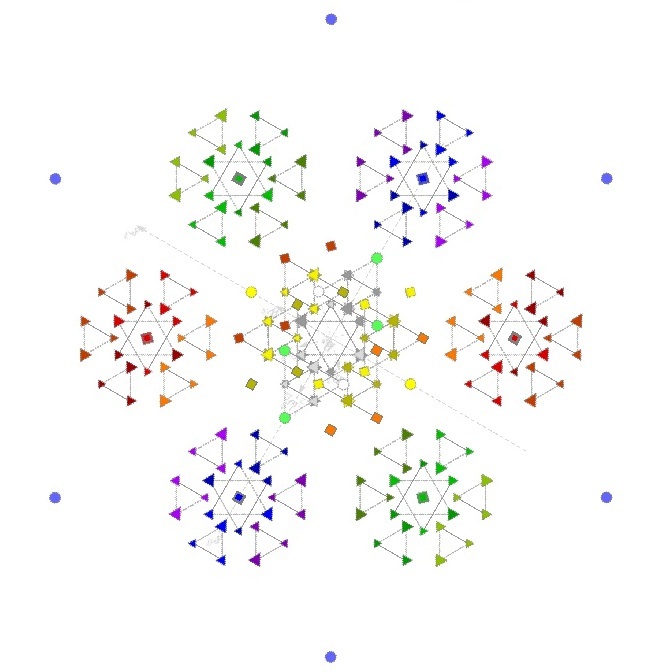
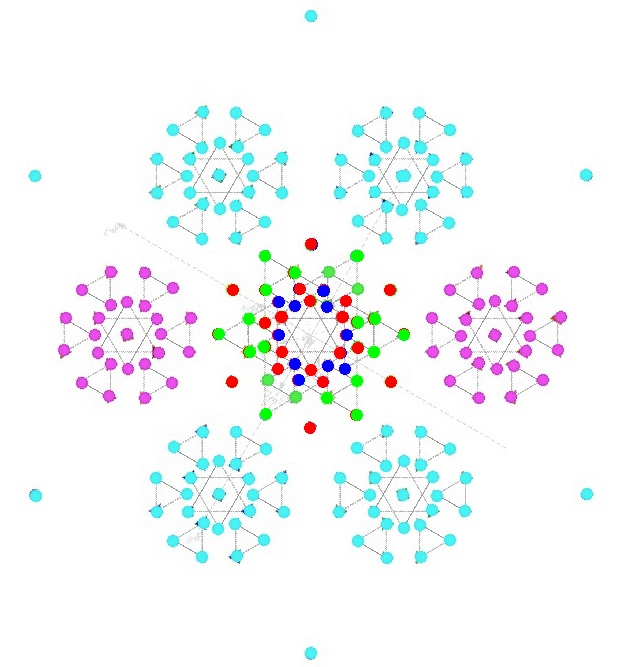
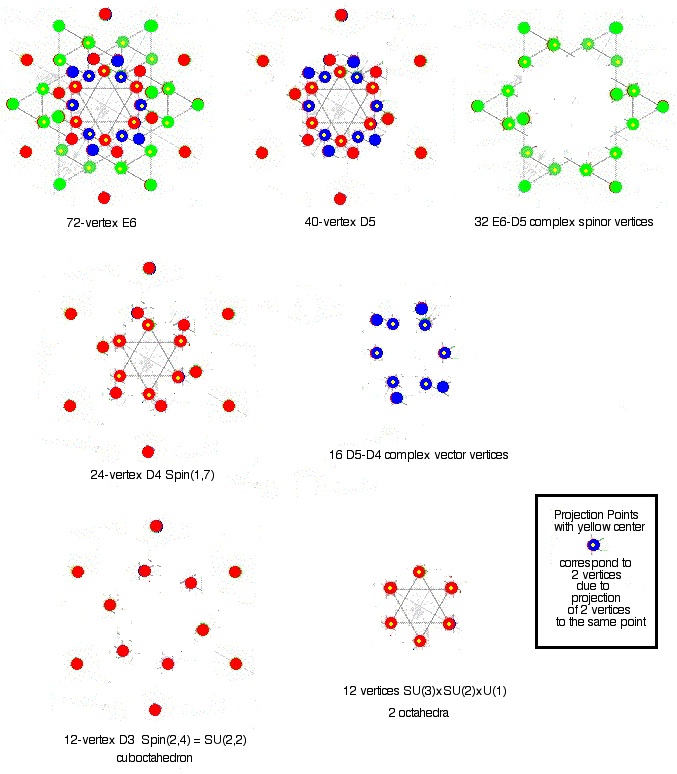
... we can find subalgebras by starting with the root system of a Lie algebra, rotating it until multiple roots match up on parallel lines, and collapsing the root system along these lines to an embedded space of lower dimension - a projection ... the central cluster of 72 roots ... is the E6 root system, which acts on each of the three colored and anti-colored 27 element clusters of the exceptional Jordan algebra ...[ J3(O) ]... the e6 subalgebra of e8 reveals how the fermions and anti-fermions ... are combined ...
[A] specific triality matrix [is] chosen to rotate between the fermion generations ... It is conceivable that there is a more complicated way of assigning three generations of fermions to the E8 roots to get standard model quantum numbers for all three generations without triality equivalence. ...
The action for everything, [is] chosen by hand to be in agreement with the standard model ...[and to be]... over a four dimensional base manifold. ... All known fields are parts of an E8 principal bundle connection in agreement with the Pati-Salam
grand unified theory, with a handfull of new fields suggested by the structure of E8 ...[and]... with gravity included via the MacDowell-Mansouri technique. The theory has no free parameters. The coupling constants are unified at high energy, and the cosmological constant and masses arise from the vacuum expectation values of the various Higgs fields ...".
To compare the E8 and Cl(8) physics models, begin with the graded structure of 256-dimensional Cl(8) and see how each Lie algebra of the series D4 - D5 - E6 - E7 - E8 can be constructed from parts of Cl(8), noting that
Note that in the above image some of the 240 E8 vertices are projected to the same point:
Since an important aspect of both the E8 model and the Cl(8) model is the representation of fermions by spinor-type structures,
such as by 8-dimensional Spin(8) +half-spinors and 8-dimensional Spin(8) -half-spinors in the Cl(8) model
and by 128-dimensional Spin(16) half-spinors in the E8 model (based on the identification of 248-dimensional E8 as the sum of the 120-dimensional Spin(16) adjoint plus a 128-dimensional Spin(16) half-spinor space)
it is useful to see how spinor-type structures appear in the above-described structure of E8 by enclosing theire enumeration in [ brackets ]:
Note that each of the [16] above live in the 27-dimensional exceptional Jordan algebra J3(O), which is the algebra of 3x3 Hermitian Octonion matrices
Re(O1) O4 O5 O4* Re(O2) O6 O5* O6* Re(O3)
where Re(Oi) is the real part (just a real number) of the i_th octonion for i = 1,2,3 and O4, O5, and O6 are full octonions, with O4 and O5 corresponding to the 8-dimensional Spin(8) +half-spinors and 8-dimensional Spin(8) -half-spinors, and O6 corresponding to the 8-dimensional Spin(8) vectors.
Given a fixed 8-dimensional Root Vector Space with Octonionic basis { 1, i, j, k, e, ie, je, ke }, the coordinates of the 240 vertices of an E8 Root Vector Polytope can be written as:
16 related to the Octonionic Basis Vectors and to the 120-8 = 112 adjoint Spin(16) Root Vectors
±1, ±i, ±j, ±k, ±e, ±ie, ±je, ±ke,
96 containing both a and ae (where a = i,j,k) related to the 120-8 = 112 adjoint Spin(16) Root Vectors
(±1 ±ke ±e ±k)/2 (±i ±j ±ie ±je)/2
(±1 ±je ±j ±e)/2 (±ie ±ke ±k ±i)/2
(±1 ±e ±ie ±i)/2 (±ke ±k ±je ±j)/2
128 containing all i,j,k types (some possibly multiplied by e) related to 128 half-spinors of Spin(16)
(±1 ±ie ±je ±ke)/2 (±e ±i ±j ±k)/2
(±1 ±k ±i ±je)/2 (±j ±ie ±ke ±e)/2
(±1 ±i ±ke ±j)/2 (±k ±je ±e ±ie)/2
(±1 ±j ±k ±ie)/2 (±je ±e ±i ±ke)/2
They generate a lattice (an E8 Lattice) that spans the 8-dimensional Root Vector Space and is consistent with Octonion Multiplication, and they are the coordinates of 240 nearest neighbors to the origin in that E8 Lattice.
None of those 240 nearest neighbors are of the form (±1±i±j±k±e±ie±je±ke)/2 (conventional light-cone form). They all appear in the next layer out from the origin of that E8 Lattice, at radius sqrt 2, which layer contains in all 2160 vertices.
The E8 set out above has 16 vertices of the form ±a and 224 vertices of the general form (±a ±b ±c ±d)/2.
Since there are ( 8 choose 4 ) = 8x7x6x5 / 1x2x3x4 = 70 sets of 4 components and 2^4 = 16 sets of signs, there are 70 x 16 = 1,120 possible 4-component vertices,
only 224 of which are used in the E8 set out above.
The other 1120 - 224 = 896 vertices are found in other independent Root Vector Polytopes of type E8.
As it turns out, there are 7 independent Root Vector Polytopes / Lattices of type E8, denoted E8_1, E8_2, E8_3, E8_4, E8_5, E8_6, E8_7. Some of them have vertices in commmon, but they are all distinct.
All of the 7 independent Root Vector Polytope Lie algebras E8_i correspond to E8 Lattices consistent with Octonion Multiplication, and the the 7 Lie algebras / Lattices / Root Vector Polytopes E8_i are related to each other as the 7 Octonion imaginaries i,j,k,e,ie,je,ke.
There are 480 different Octonion Multiplication rules, but all 7! permutations of the 7 Octonion imaginaries do not give distinct Octonion Multiplications since Octonion Multiplication has symmetry group PSL(2,7) = of order 168.
The 240 - 72 =168 vertices outside the central E6
correspond to 6 copies of 27-dimensional J3(O) plus a single vertex.
In the Cl(8) model, each of the 6 copies of J3(O)+1 is a link to the other 6 E8_i Lie algebras, and the fact that the 6 copies of J3(O)+1 have 168 elements may be related to the symmetry of Octonion Multiplication of the 7 Octonion imaginaries, corresponding to the 7 Lie algebras E8_i,
and
the physical use of the 7 independent E8_i in the Cl(8) model is in constructing D8 branes in a Bosonic String Theory with Fermions coming from Orbifolding, but without conventional supersymmetry ( see CERN preprint CERN-CDS-EXT-2004-031 and my web page at www.valdostamuseum.org/hamsmith/stringbraneStdModel.html ).
The 168-element symmetry is also related to the Klein Quartic .
Garrett Lisi describes the physics of the E8 model as
"... The action for everything, [is] chosen by hand to be in agreement with the standard model ...
The Cl(8) model Lagrangian is entirely made up of components from the Cl(8) Cifford algebra with graded structure
Dimensional reduction of physical spacetime to 4 dimensions comes from freezing out at low (our present experimental) energies of a preferred quaternionic subspace of the octonionic 8-dimensional spacetime, and the process produces:
The E8 base manifold is an ad hoc 4-dimensional addition to 248-dimensional E8,
while
the Cl(8) base manifold is a natural part (8-dimensional vector space) of 256-dimensional Cl(8).
One possibility might be to let the E8 base manifold go to 8 dimensions, as in the 4+4 = 8 dimensional Kaluza-Klein Spacetime described by N. A. Batakis in Class. Quantum Grav. 3 (1986) L99-L105, which was successful with respect to the Standard Model gauge bosons and was not generally accepted because of difficulties of adding fermions. Perhaps the boson-fermion structure of E8 could solve those difficulties of the Batakis model. By combining the 248 E8 dimensions with the 8 Batakis Kaluza-Klein spacetime dimensions, you could form the 256 dimensional Cl(8) Clifford algebra, whose structure could be used as a guide for naturally constructing a Lagrangian that could reproduce the successes of the Standard Model and Gravity based on MacDowell-Mansouri.
A problem might be that the 8 extra-from-E8 dimensions of Cl(8) seem to be structurally part of the 70-dimensional 4-vector part of Cl(8) and not in the 8-dimensional vector part of Cl(8).
The triality generation mechanism of the E8 model is substantially different from the dimensional reduction mechanism of the Cl(8) model, but Garrett Lisi does say that "... It is conceivable that there is a more complicated way [ than the E8 model triality ] of assigning three generations of fermions ...".
The Cl(8) model uses Spin(8) Triality to establish a subtle supersymmetry between Fermions (8-dimensional +half-spinors and 8-dimensional -half-spinors) and Bosons (bivectors constructed from 8-dimensional vectors),
while
The E8 model uses Triality to get 3 generations of Fermions.
The Cl(8) model uses the 7 independent E8_i in constructing D8 branes in a Bosonic String Theory with Fermions coming from Orbifolding, but without conventional supersymmetry ( see CERN preprint CERN-CDS-EXT-2004-031 and my web page at www.valdostamuseum.org/hamsmith/stringbraneStdModel.html ),
while Garrett Lisi said in a comment on Bee's blog entry about his E8 model "... LQE8 theory or whatever one wants to call it would be a competitive ToE, vying with strings ...".
The Cl(8) model has a highly developed system of calculating particle masses and force strengths, etc. For an outline, see my web page at www.valdostamuseum.org/hamsmith/July2006Update.html#octuninflation .
The Cl(8) model also permits calculation of
Details are on my web site at www.valdostamuseum.org/hamsmith/
Both the E8 and Cl(8) models produce the non-supersymmetric Standard Model.
Both the E8 and Cl(8) models use the MacDowell-Mansouri mechanism to produce Gravity.
Both the E8 and Cl(8) models use spinor-type representations of Spin groups that are naturally within the defining structures of E8 and Cl(8).
The Spin(16) of E8 and the Spin(8) of Cl(8) are related as follows: consider the graded structure of Cl(8)
and that by periodicity Cl(16) = Cl(8) (x) Cl(8) so that the 120 SO(16) bivectors of Cl(16) should be made up of three parts:
to get the 28+28+64 = 120-dim SO(16) bivector algebra of Cl(16) = Cl(8) (x) Cl(8).
Garrett Lisi said in comments on Bee's blog entry about his E8 model, and in his paper 07110770, "... The primary LQG program is a search for a successful method for describing a background independent, quantum theory of a connection -- the connection of gravity. What this E8 theory does is include all fields in a large connection. So, combined, LQE8 theory or whatever one wants to call it would be a competitive ToE, vying with strings ... ...
... The 26 is the traceless [ part of the ] exceptional Jordan algebra ... the central cluster of 72 roots in ...[ the E8 root vector polytope ]... is the E6 root system, which acts on each of the three colored and anti-colored 27 element clusters of the exceptional Jordan algebra ...
In a spin network the edges carry representation labels for gravity and gauge fields, while the vertices (nodes) are labeled by numbers for the fermions. Since, in a sense, all the fields in this theory I [ Garrett Lisi ] presented are E8 gauge fields, including the fermions, this would mean that all the representation labels would be on the edges ...".
Both the E8 model and the Cl(8) model contain structures of the 27-dimensional exceptional Jordan algebra J3(O) and, consequently, its 26-dimensional traceless part J3(O)o.
John Baez said on sci.physics.research on 16 Jan 2001 ( here I change some notation ): "... The quotient of Lie algebras e6 / f4 is a vector space that can be naturally identified with J3(O)o. That's really cool! But the quotient of Lie groups E6 / F4 is what matters for the spin foam models, and this is a bit "curvier" - it has a natural metric that's not flat. They are closely related, however: e6/f4 can be viewed as a tangent space of E6 / F4. ...". John Baez then quoted my earlier post saying that I "... would like very much to be told how such a construction goes, because in my opinion such a J3(O)o spin foam model should lead to, not just quantum gravity, but a Theory Of Everything. ..." and John Baez replied to that saying: "... Shhh! That's supposed to be secret. :-) Yes, of course something like this is my goal, but I'm not eager to count my chickens before they are hatched, nor take my ideas to market while they're still half-baked. ...". So, although unification of LQC spin foams with E8 containing copies of 26-dimensional J3(O)o may be (as John Baez indicated) not yet fully baked, it is an idea that knowledgeable people such as John Baez have as a goal.
To use the E8 model for a spin foam, it might be useful to ignore the ad hoc 4-dimensional base manifold and to use only E8 structure by
and seeing what dimensionality emerges from such a network.
To use the Cl(8) model for a spin foam, basic structures might be E6, Spin(8) adjoint, vector, and half-spinors, and J3(O) with E8 lattices related to D8 branes, along with 4-dimensional Feynman Checkerboard structures ( see my web page at www.valdostamuseum.org/hamsmith/USGRFckb.html ).
The resulting spin foams may turn out to be similar, since Spin(16) and Spin(8) are related through the real Clifford periodicity tensor product factorization
Garrett Lisi said (in comments to Bee's blog entry about the E8 model) that a "... condition ...[of]... the Coleman-Mandula theorem ... is that there needs to be a Poincare' subgroup. There is no Poincare' subgroup in this E8 theory. ... The G = E8 I [Garrett Lisi] am using does not contain a subgroup locally isomorphic to the Poincare group, it contains the subgroup SO(4,1) -- the symmetry group of deSitter spacetime. ...this theorem does not apply in this case. ...".
However,
Steven Weinberg showed at pages 12-22 of his book The Quantum Theory of Fields, Vol. III (Cambridge 2000) that Coleman-Mandula is not restricted to the Poincare Group, but extends to the Conformal Group as well.
Since the Conformal Group SO(4,2) contains Garrett's de Sitter SO(4,1) as a subgroup, it seems to me that it is incorrect to claim that use of deSitter SO(4,1) means that Coleman-Mandula "... does not apply ..." to the E8 model.
However, it may be that an E8 model could be (for other reasons) consistent with Coleman-Mandula.
With respect to Coleman-Mandula (particularly with respect to fermions) it is useful to consider what Bee said: "... the five exceptional Lie-groups have the remarkable property that the adjoint action of a subgroup is the fundamental subgroup action on other parts of the group. This then offers the possibility to arrange both, the fermions as well as the gauge fields, in the Lie algebra and root diagram of a single group ..." and what Steven Weinberg said at pages 382-384 of his book The Quantum Theory of Fields, Vol. III (Cambridge 2000):
"... The proof of the Coleman-Mandula theorem ... makes it clear that the list of possible bosonic symmetry generators is essentially the same in d greater than 2 spacetime dimensions as in four spacetime dimensions:... there are only the momentum d-vector Pu, a Lorentz generator Juv = -Jvu ( with u and v here running over the values 1, 2, ... , d-1, 0 ), and various Lorentz scalar 'charges' ...
the fermionic symmetry generators furnish a representation of the homogeneous Lorentz group ... or, strictly speaking, of its covering group Spin(d-1,1). ...
The anticommutators of the fermionic symmetry generators with each other are bosonic symmetry generators, and therefore must be a linear combination of the Pu, Juv, and various conserved scalars. ...
the general fermionic symmetry generator must transform according to the fundamental spinor representations of the Lorentz group ... and not in higher spinor representations, such as those obtained by adding vector indices to a spinor. ...".
In short, Weinberg's book at pages 382-384 says that the important thing about Coleman-Mandula is that fermions in a unified model must "... transform according to the fundamental spinor representations of the Lorentz group ... or, strictly speaking, of its covering group Spin(d-1,1). ..." where d is the dimension of spacetime in the model.
As I said in that comment, E8 is the sum of the adjoint representation and a half-spinor representation of Spin(16), so,
if the E8 model is built with respect to Lorentz, spinor, etc representations based on Spin(16) consistently with Weinberg's work,, then the E8 model may be consistent with Coleman-Mandula.
The Cl(8) model is, due to compliance with the criteria set out by Weinberg, consistent with Coleman-Mandula ( see my web page at www.valdostamuseum.org/hamsmith/d4d5e6hist2.html#ColemanMandula )
With respect to the figure

As to the first and third circles from the center, which have 12 points, to each of which 2 vertices are projected, so that each circle represents 24 vertices, the four circles together appear (in the projection)
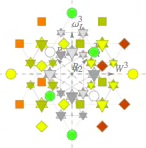
to have a total of 12 + 12 + 12 + 12 = 48 vertices, but a further rotation taken from an E8 rotation movie by Garrett Lisi (as is the image immediately above)
shows that in fact the configuration has 16 + 40 + 16 = 48 + 12 + 12 = 72 vertices, the correct number for the E6 root vector polytope.
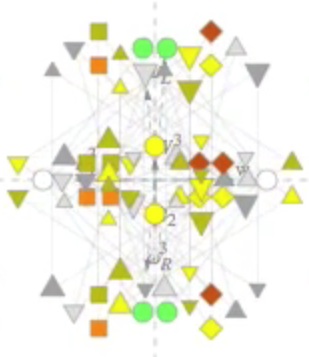
As to the central point of each of the 6 clusters corresponding to the 27-dimensional exceptional Jordan algebra J3(O), to each of which 3 vertices are projected, so that each cluster represents 27 vertices, the two concentric 12-vertex circles and the center point appear (in the projection)
to have a total of 12 + 12 + 1 = 25 vertices, but a further rotation taken from an E8 rotation movie by Garrett Lisi (as is the image immediately above)

shows that in fact the configuration has 1 + 16 + 10 = 12 + 12 + 3 = 27 vertices, the correct number for the dimension of the exceptional Jordan algebra J3(O).
Garrett, this is a long comment (see my PS at the end), but the short version is: It seems to me that Jacques Distler did not refute your E8 model (only a possible use of triality) and that his analysis, along with your comments, show how the E8 model can be OK. Here are details: Distler said in his blog: "... E8(8) includes Spin(16) as a maximal compact subgroup ... In E8(8), the 248 decomposes as 248 = 120 + 128 ... We would like to find an embedding of G = SL(2,C) x SU(3)xSU(2)xU(1) in ... E8 ... SL(2,C) = Spin(3,1)o is the connected part of the Lorentz Group, the "gauge group" in the MacDwoell-Mansouri formulation of gravity. ..." and you [Garrett] replied "... The G is embedded in a D4 x D4 subgroup of E8. ... g = so(3,1) + su(2) + u(1) + su(3) ... is in a so(7,1) + so(8) of e8 via the Pati-Salam, left-right symmetric model, g' = so(3,1) + su(2)_L + su(2)_R + su(4) The so(3,1) + su(2)_L + su(2)_R is in so(7,1), the su(4) is in so(8) ..." and Distler said "... Spin(7,1) x Spin(8) ... is a subgroup of E8(8) ...". So, an E8(8) model should be OK with the following interpretation: e8(8) = 120 + 128 120 = spin(16) = spin(8) + 64 + spin(7,1) = 28 + 64 + 28 128 = 64 + 64 where gravity comes from spin(3,1) MacDowell-Mansouri and the Standard Model comes from Pati-Salam su(4)_c + su(2)_L + su(2)_R spin(8) includes su(4) that reduces to su(3)_c spin(7,1) includes so(3,1) + su(2)_L + su(2)_R where the so(3,1) of MacDowell-Mansouri gravity is the little group, or local isotropy group, of 4-dim spacetime M4 described by the symmetric space G / Spin(3,1) where G can be anti-desitter or deSitter and where the su(2)_L + su(2)_R reduces to su(2)_L + u(1) which is the little group of a 4-dim internal symmetry space CP2 = SU(3) / SU(2)xU(1) NOTE that the Lie groups of the spin(7,1) Lie algebra form the little groups of an 8-dim M4 x CP2 Kaluza-Klein space (as used by Batakis in his 1986 paper Class. Quantum Grav. 3 (1986) L99-L105). As to the global groups of M4 x CP2, they are in the spin(8) that includes the su(4): the su(3) gives the global group SU(3) in CP2 = SU(3) / SU(2)xU(1) (as used by Batakis) and the 4-dimensional deSitter or anti-deSitter rotations of G / Spin(3,1) should be a part of 6-dim twistor-related CP3 = SU(4) / SU(3)xU(1) What about the one 64 in the 120 and the two 64 + 64 in the 128 of E8(8) ? Each of the 64 should be of the form 8x8. Generalizing the spacetime algebra approach of Hestenes, let, in each of the three 64, one of the 8 represent 8 Dirac Gammas of the 8-dim K-K space. Denote it by 8_G Since the 64 in the 120 is in the adjoint of Spin(16), its 8x8 should be correspond to the 8-dim vector K-K space, so denote the 64 in 120 by 8_v x 8_G Since the 64 + 64 in the 128 is in a spinor space of Spin(16), its 8x8 + 8x8 should be correspond to fermions ( 8 particles and 8 antiparticles) so denote the 128 64 + 64 in 128 by 8_f+ x 8_G and 8+f- x 8_G There should be a Spin(8)-type triality among the three 64 things 8_v x 8_G 8_f+ x 8_G 8+f- x 8_G The above E8(8) structure describes Gravity, the Standard Model, 4-dim physical spacetime, a 4-dim K-K space, and first-generation fermions, as well as 8 Gammas of an 8-dim Dirac equation. If the second and third generation fermions come from combinatorics of fermions living partly in 4-dim physical spacetime and partly in 4-dim K-K space, then you get all three generations. My opinion is that: a spin foam can be constructed by putting the 120 of E8(8) on links and the 128 of E8(8) on vertices, and using Jordan algebra structure related to the 27-dim exceptional Jordan algebra J3(O); and particle masses and force strengths come from ratios of geometric volumes in the spirit of Armand Wyer; neutrinos are tree-level massless, with masses coming from corrections; Dark Energy : Dark Matter : Ordinary Matter ratio comes from the structure of the twistor stuff in the spin(8) of the 120. Tony Smith PS - Sorry for the long post on mauitian. If you want me to not put such stuff here, please just let me know.
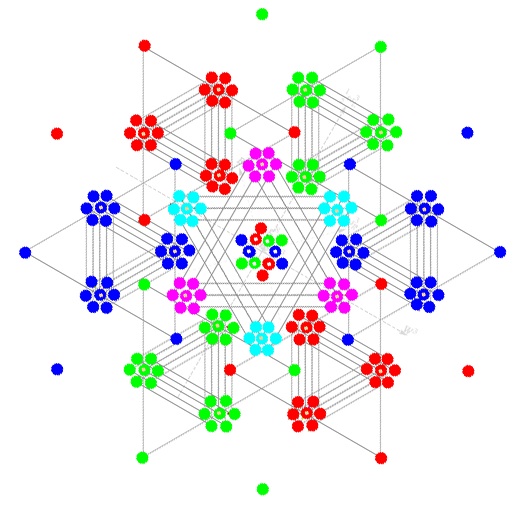
Note that in the above image some of the 240 E8(8) vertices are projected to the same point:
Note also that here (to be consistent with Garrett Lisi's notation) I am using a notation Spin(7,1) that differs from what I usually use, which is Spin(1,7).
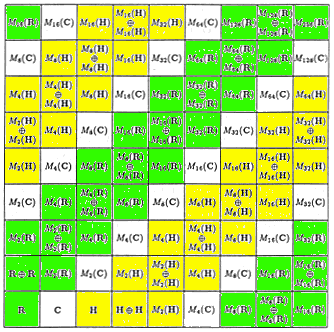
Note also that (in my usual notation) Spin(1,7) comes from Cl(1,7) which the 16x16 real matrix algebra and so is isomorphic to Cl(0,8) = Cl(8).