E8 Lie Algebra from Clifford Algebra Cl(8)

and also D4-D5-E6-E7-E8 of my VoDou Physics Model, as well as B4 and F4

The Clifford Algebra Cl(8) has dimension 2^8 = 256.

Since 256 = 16 x 16 = 2^4 x 2^4, the full spinors of Cl(8) are 16-dimensional, and the half-spinors of Cl(8) are 8-dimensional.

Cl(8) has graded structure

1   8  28  56  70  56  28   8   1

The 28-dimensional grade-2 bivectors of Cl(8) form the Lie Algebra Spin(8).

The E8 Lie Algebra is the sum (on this page I am using the word "sum" very imprecisely) of

the 120-dimensional Spin(16) Lie Algebra of the 2^16 = 256 x 256 = 65,536-dimensional Cl(16) Clifford Algebra

and

one 2^7 = 128-dimensional Cl(16) half-spinor space.

To construct E8 from Cl(8):

First, construct the 120-dimensional Spin(16) from Cl(8):

Since Cl(16) can be written as the tensor product Cl(16) = Cl(8) x Cl(8), the graded structure of Cl(16) can be written in terms of the graded structure of Cl(8) as follows:

1     8    28    56    70    56    28     8     1
      8    64   224   448   560   448   224    64     8
           28   224   784  1568  1960  1568   784   224    28
                 56   448  1568  3136  3920  3136  1568   448    56
                       70   560  1960  3920  4900  3920  1960   560    70
                             56   448  1568  3136  3920  3136  1568   448    56
                                   28   224   784  1568  1960  1568   784   224    28
                                          8    64   224   448   560   448   224    64     8
                                                1     8    28    56    70    56    28     8     1

1    16   120   560  1820  4368  8008 11440 12870 11440  8008  4368  1820   560   120    16     1

Therefore:

Spin(16) = 120 = 28x1 + 8x8 + 1x28 = 28 + 64 + 28, and

Spin(16) is the sum of two copies of Spin(8)

plus the square of the 8-dimensional Cl(8) grade-1 vector space.

Second, construct the 128-dimensional half-spinors of Cl(16) from Cl(8):

The Cl(8) half-spinors are 8-dimensional, so that the Cl(8) full-spinor space is 8e + 8o = 16-dimensional, where 8e is one half-spinor 8-dimensional space and 8o is the other mirror image half-spinor 8-dimensional space.

ou can construct the spinor space of Cl(16) as the tensor product ( 8e + 8o ) x ( 8e + 8o ) as follows:

8ex8e  +  8ex8o          
          8ox8e  +  8ox8o

If ee and oo correspond to e, and if eo and oe correspond to o, we have:

64e   + 128o  +   64e

so that the Cl(16) spinors are (64 + 64)e + 128o = 256-dimensional, and

the Cl(16) half-spinors are 128-dimensional and are the sum of the squares of the two 8-dimensional Cl(8) half-spinor spaces.

Therefore:

248-dimensional E8 is the sum of

two copies of 28-dim Spin(8)

plus

the 64-dim square of the 8-dimensional Cl(8) grade-1 vector space

plus

the sum of the 64-dim squares of the two 8-dimensional Cl(8) half-spinor spaces.

and

256-dimensional Cl(8) is the sum of

248-dim E8

plus

the 8-dim vector space of Cl(8).

E8 is the sum of 28-dim Spin(8) plus Octonionic versions of the two 8-dim half-spinor spaces of Cl(8) and the 8-dim vector space of Cl(8), each of which is 8x8 = 64-dimensional.

The second 28-dimensional Spin(8) corresponds to the Octonionic Spin(8) symmetries of each of the two half-spinor spaces and of the vector space. Note that the same Octonionic Spin(8) is used for each of the two half-spinor spaces and for the vector space, as is consistent with the fact (noted by Geoffrey Dixon in his book on Divison Algebras) that the left-adjoint and right-adjoint actions of the Octonions are both isomorphic to each other, and are also isomorphic to the 8x8 matrix algebra over a real 8-dim vector space.

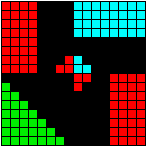
What about D4-D5-E6-E7-E8 of my VoDou Physics Model, as well as B4 and F4 ?

Here is the analogous pattern for 133-dimensional E7:

E7 is the sum of 28-dim Spin(8) plus Quaternionic versions of the two 8-dim half-spinor spaces of Cl(8) and the 8-dim vector space of Cl(8), each of which is 4x8 = 32-dimensional.

The central 9 elements correspond to the Quaternionic SU(2) symmetries of each of the two half-spinor spaces and of the vector space. Note that distinct Quaternionic SU(2)s are used for each of the half-spinor spaces, as is consistent with the fact (noted by Geoffrey Dixon in his book on Divison Algebras) that the left-adjoint and right-adjoint actions of the Quaternions are not isomorphic to each other, nor are they 4x4 matrix algebras over a real 4-dim vector space.

Here is the analogous pattern for 78-dimensional E6:

E6 is the sum of 28-dim Spin(8) plus Complex versions of the two 8-dim half-spinor spaces of Cl(8) and the 8-dim vector space of Cl(8), each of which is 2x8 = 16-dimensional.

The central 2 elements correspond to the Complex U(1) symmetries of the spinor spaces and of the vector space. Note that the same Complex U(1) is used for both of the half-spinor spaces, as is consistent with the fact (noted by Geoffrey Dixon in his book on Divison Algebras) that the left-adjoint and right-adjoint actions of the Complex numbers are both isomorphic to each other, but are not 2x2 matrix algebras over a real 2-dim vector space.

Here is the analogous pattern for 45-dimensional D5:

D5 is the sum of 28-dim Spin(8) plus a Complex versions of the 8-dim vector space of Cl(8), which is 2x8 = 16-dimensional. D5 is the Spin(10) Lie algebra of the Clifford Algebra Cl(10), which factors by tensor product into Cl(10) = Cl(2) x Cl(8). Since the graded structure of Cl(2) is 1 + 2 + 1, the graded structure of Cl(10) is

1     8    28    56    70    56    28     8     1
      2    16    56   112   140   112    56    16     2
            1     8    28    56    70    56    28     8     1

1    10    45   120   210   252   210   120    45    10     1

The 1 of the 45 corresponds to the grade-2 bivector of Cl(2), acting as U(1) on the 2-dim vector space of Cl(2). It is represented on the pattern by the central element corresponding to the Complex U(1) symmetry of the Complex version of the Cl(8) vector space.

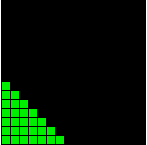
Here is the analogous pattern for 28-dimensional D4:

D4 is the 28-dim Spin(8) of the Cl(8) Clifford Algebra with graded structure

1 8 28 56 70 56 28 8 1

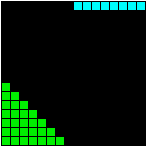
Here is the analogous pattern for 36-dimensional B4:

B4 is the sum of 28-dim Spin(8) plus the 8-dim vector space of Cl(8). B4 is the Spin(9) Lie algebra of the Clifford Algebra Cl(9), which factors by tensor product into Cl(9) = Cl(1) x Cl(8). Since the graded structure of Cl(1) is 1 + 1, the graded structure of Cl(9) is

1     8    28    56    70    56    28     8     1
      1     8    28    56    70    56    28     8     1

1     9    36    84   126   126    84    36     9     1

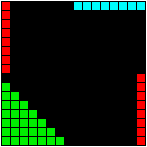
Here is the analogous pattern for 52-dimensional F4:

F4 is the sum of 28-dim Spin(8) plus the two 8-dim half-spinor spaces of Cl(8) and the 8-dim vector space of Cl(8).

Note that the 16-dimensional symmetric space F4 / Spin(9) is the Octonion Projective Plane, which is represented on the pattern by the two 8-dim half-spinor spaces of Cl(8).

I repeat that on this page I have used the word "sum" very imprecisely.

Tony Smith's Home Page

......