Tony Smith's Home
Page
What ARE Loopoids ?
Groupoids
Unfortunately, in the mathematics literature there are two
very different definitions of "groupoid". One, that I do NOT like to
use, is definition number 1 in Eric Weisstein's Encyclopedia of
Mathematics: "... an algebraic structure on a set with a binary
operator. The only restriction is closure ...".
The definition that I like to use is given by Alain Connes in his
book Noncommutative Geometry:
"... a groupoid G ... a small categrory with inverses ... consists
of
- a set G,
- a distinguished subset G0 of G,
- two maps r, s : G -> G0 and
- a law of composition o : G2 = {(g1,g2) in G x G ; s(g1) =
r(g2)} -> G
such that
- (1) s(g1 o g2) = s(g2) , r(g1 o g2) = r(g1) for all (g1,g2) in
G2
- (2) s(x) = r(x) = x for all x in G0
- (3) g o s(g) = g , r(g) o g = g for all g in G
- (4) (g1 o g2) o g3 = g1 o (g2 o g3)
- (5) Each g has a two-sided inverse g-1 , with g g-1 = r(g) ,
g-1 g = s(g)
The maps r,s are called the range and source maps. ... Here are a
few important examples of groupoids. ...
- Given a group P one takes G = P , G0 = {e}, and the law of
composition is the group law. ...
- A Lie group G is, in a trivial way, a groupoid with G0 = {e}.
...
- The groupoid G = M x M where M is a compact manifold, r and s
are the two projections G -> M = G0 = {(x,x) ; x in M} and the
composition is (x,y) o (y,z) = (x,z) for all x,y,z in M.
...".
Alan Weinstein says in his paper Groupoids:
Unifying Internal and External Symmetry:
"... a groupoid with base B is a set G with mappings a and b from
G onto B with a partially defined binary operation (g,h) --> gh
satisfying ...
- gh is defined only when b(g) = a(h) ...
- if either of the products (g h) k or g (h k) is defined, then
so is the other, and they are equal [associativity]
...
- For each g in G, there are left and right identity elements Lg
and Rg such that Lg g = g = g Rg ...
- Each g in G has an inverse g-1 for which g g-1 = Lg and g-1 g
= Rg ...
... We may think of each element g of G as an arrow pointing from
b(g) to a(g) in B; arrows are multiplied by placing them head to tail
... a(b) and Lg ( or b(g) and Rg) determine one another, thus
producting a bijective mapping I from the base B to the subset G0 of
G consisting of the identity elements. ...
... a groupoid is just a ... small ... category in which every
morphism has an inverse ...
... An orbit of the groupoid G over B is an equivalence class for
the relation x ~G y if and only if there is a groupoid element g with
a(g) = x and b(g) = y ...
... The isotropy group of x [in] B consists of those g in
G with a(g) = x = b(g) ...".
The groupoid picture is something like
G
| |
r| |s
| |
\/ \/
G0
John Baez,
on his web page at week74
and related pages, describes groupoids and applies them to category
theory.
Another way that a groupoid usefully generalizes a group is that
by taking G0 to be a larger subset of G than the singleton identity
{e}, you can use a multiplication law (such as the Octonion
x-product and xy-product) that varies over the underlying base
space G0.
However, as John
Baez pointed out to me in September 2003 e-mail messages,
when you try to use a Groupoid to describe the 7-sphere S7 of unit
Octonions, you are prevented by groupoid axiom (4), which requires
associativity of a groupoid composition law, and therefore prevents
use of S7's natural nonassociative Octonion
multiplications.
Moufang Loops and Malcev Algebras
If you want to use nonassociativity, you can consider Moufang
Loops.
Jaak Lohmus, Eugene Paal, and Leo Sorgsepp, in their book
Nonassociative Algebras in Phyiscs (Hadronic Press 1994), say:
"... Moufang loops and Mal'tsev [another
transliteration for "Malcev"] algebras ... are ... natural
(minimal) generalizations of Lie groups and Lie algebras,
respectively. Because of the uniqueness of octonions ...
octonionic Moufang loop and the corresponding simple (non-Lie)
Mat'tsev algebra are of exceptional importance ...
A Moufang loop is a set G with a binary operation
(multiplication) ... so that ...
- 1) in the equation g h = k, the knowledge of any two of
g,h,k [in] G specifies the third one uniquely;
- 2) there is a distinguished unit or identity element e of G
with the property e g = g e = g, [for all] g
[in] G;
- 3) the Moufang identity holds: (g h)(k g) = g((h k)g),
[for all] g,h,k [in] G.
A set with such a binary operation that only axioms 1/ and 2)
are satisfied is called a loop. ... roughly speaking, loops are
the "nonassociative groups". ... The most remarkable property
of Moufang loops is their diassociativity: the subloop generated
by any two elements in a Moufang loop is associative (group).
Hence, for any g,h in a Moufang loop G ... (h g)g = h g^2 , g(g h)
= g^2 h , (g h)g = g(h g) ... thanks to [which]... the
Moufang identity can be written ... (g h)(k g) = g(h k) g.
... one can define the notion of the inverse element of g
[in] G. The unique solution of the equation g x = e (x g =
e) is called the right (left) inverse element of g [in] G
and denoted as g-1R (g-1L). From ... diassociativity ... g-1R =
g-1L = g-1 , g-1(g h) = (h g)g-1 = h , (g-1)-1 = g , (g h)-1 = h-1
g-1 ; [for all] g,h [in] G.
... The Moufang loop G is said to be analytic if G is a real
analytic manifold so that both the Moufang lop operation G x G
--> G : (g,h) --> g h and the inversion map G --> G : g
--> g-1 are analytic ... denote the dimension of G by r ...
introduce the antisymmetric quantities
c^i_jk := a^i_jk - a^i_kj ... i,j,k = 1, ... , r ,
called the structure constants of G. ... The tangent algebra
G of G ...[with]... product
[X,Y]^i := c^i_jk X^j Y^k = -[Y,X]^i ; i,j,k =
1, 2, ... , r .
...[with the]... Mal'tsev identity ...
[[X,Y],[Z,X]] +
[[[X,Y],Z],X] +
[[[Y,Z],X],X] +
[[[Z,X],X],Y] = 0
... is ... the ... Mal'tsev algebra. ... the Jacobi identity
...[may fail] in G...
... every Lie algebra is a Mal'tsev algebra ... In a Mal'tsev
algebra G the Yamaguti triple product ... may be
defined as ...
[x,y,z] := [x,[y,z]] -
[y,[x,z]] + [[x,y],z]
... K. Yamaguti proved ... the possibility of embedding a
Mal'tsev algebra into a Lie algebra ... every Mal'tsev algebra can
be realized as a subspace of some Lie algebra so that the Mal'tsev
operation is a projection of the Lie algebra operation to this
subspace. ...
.... Every Mal'tsev algebra is also a ... Lie triple system ...
Lie triple systems ... serve as tangent algebras for symmetric
spaces ...
S7 Moufang Loop
According to the paper Analytic Loops and Gauge Fields by E. K.
Loginov at hep-th/0109206:
"... simple nonassociative Moufang loops
...[are]... analytically isomorphic to one of the spaces
S7, S3 x R4, or S7 x R7 ...
... Suppose A is a complex (real) Cayley-Dickson algebra, M is
its commutator Malcev algebra, and L(A) is the enveloping Lie
algebra of regular representation of A.
It is obvious that the algebra L(A) is generated by the
operators Rx and Lx, where x [is in] A. We select in L(A)
the subspaces R(A), L(A), S(A), P(A) and D(A) generated by the
operators
- Rx,
- Lx,
- Sx = Rx + 2Lx,
- Px = Lx +2Rx and
- Dx,y = [Tx, Ty]+T[x,y],
where Tx = Rx -Lx, accordingly. ...
[Rx, Sy] = R[x,y] ...[and]... [Lx,
Py] = L[y,x].
... the algebra L(A) is decomposed into the direct sums
- L(A) = D(A) + S(A) + R(A),
- L(A) = D(A) + P(A) + L(A),
of the Lie subalgebras D(A) + S(A), D(A) + P(A) and the vector
spaces R(A), L(A) ... In addition, the map x --> Sx from M into
S(A) is a linear representation of the algebra M, which transforms
the space R(A) into M-module that is isomorphic ... to the regular
Malcev M-module. ...
... the direct summands ... are orthogonal with respect to the
scalar product tr{XY} on L(A) ...
...Let A be the complex Cayley-Dickson algebra [of
Octonions]. Then A supposes the base 1, e1, ..., e7 such
that
ei ej = -delta_ij + c_ijk ek,
where the structural constants c_ijk are completely
antisymmetric and different from 0 only if
c_123 = c_145 = c_167 = c_246 = c_257 = c_374 = c_365 = 1.
It is easy to see that in such base the operators
- Rei = e[i0] - (1/2) c_ijk e[jk] ,
- Lei = e[i0] + (1/2) c_ijk e[jk] ,
where e[uv] are skew-symmetric matrices 8 x 8 with the
elements (euv)ab = delta_ma delta_nb - delta_mb delta_na . Using
the identity
c_ijk c_mnk = delta_im delta_jn - delta_in delta_jm + c_ijmn
,
where the completely antisymmetric tensor c_ijkl is defined by
the equality
(ei,ej,ek) = 2 c_ijkl el ,
we have D_ei,ej = 8 e[ij] + 2 c_ijmn e[mn] .
...
... Its enveloping Lie algebra L(A) (in fixed base) consists of
real skew-symmetric 8 x 8 matrices. Therefore we can connect every
element F = F_mn e[mn] of L(A) with the 2-form F = F_mn
dx^m /\ dx^n . ... the factors of F are such that
epsilon F0i + (1/2) c_ijk F_ jk = 0 ,
if F [is in] S(A) + D(A) ...[or]... P(A) + D(A)
epsilon F0i = c_ijk F_ jk ,
if F [is in] R(A) ...[or]... L(A)
where there is no summing over j,k in [the second
equations], c_ijk 6= 0, and
- epsilon = 0, if F [is in] D(A),
- epsilon = 1, if F [is in] S(A) + D(A), F [is
not in] D(A) or F [is in] R(A),
- epsilon = -1, if F [is in] P(A) + D(A), F [is
not in] D(A) or F [is in] L(A).
For epsilon = -1 these are precisely the (anty-self-dual)
equations of Corrigan et al. ... In addition, R(A) and L(A) are
not Lie algebras. Therefore the [second] equations, in
contrast to [the first equationa], are not Yang-Mills
equations. Nevertheless, there are a solution of the
[second] equations, which generalizes the known
(anty-)instanton solution of Belavin et al. ...".
Jaak Lohmus, Eugene Paal, and Leo Sorgsepp, say, further, in their
book Nonassociative Algebras in Phyiscs (Hadronic Press 1994):
"... The generators for the 8-dimensional irreps of the
algebra D4 [of Spin(8) and SO(8)] in terms of the regbirep
matrices of octonions ... can be written ... [f]or vector
representation 8v ... as follows:
- Gij = [ Li + Ri , Lj + Rj ]; i,j = 1,2, ... ,
7;
- Gij ej = ei , Gij ei = -ej , Gij ek = 0 ; i=/= j =/= k
...
... The generators for halfspinor irreps may be represented as
follows:
- {Lij} : Li0 x = Li x = ei x , Lij x = Lj Li x = ej (ei x)
,
- {Rij} : Ri0 x = Ri x = x ei , Rij x = Rj Ri x = (x ei) ej
.
Low-dimensional IRs of SO(8)
... Branching rules ...
IR ... SO(7) ... G2 ... SU(3)/Z3
1 ... 1 ... 1 ... 1
8v ... 1,7 ... 1,7 ... 8
8s1 ... 8 ... 1,7 ... 8
8s2 ... 8 ... 1,7 ... 8
28 ... 7,21 ... 7,7,14 ... 8,10,10bar
35 ... 1,7,27 ... 1,7,27 ... 8,27
35' ... 35 ... " ... "
35'' ... 35 ... " ... "
56 ... 21,35 ... 1,7,7,14,27 ... 1,8,10,10bar,27
56' ... 8,48 ... " ... "
56'' ... 8,48 ... " ... "
The subgroup SO(7) does not alter the unit element e0 ( 8v
--> 1 + 7 ), automorphisms form a still narrower subgroup G2
[of] SO(7). In the transition to the subgroup SO(7) from
generators of SO(8) the generators L0i (R0i) separate, forming the
Mal'tsev algebra M7 with the multiplication
[L0i * Lj0] = Li0 * Lj0 - Lj0 * Li0 ,
where the *-multiplication is defined by ... Lx Ly +
[Lx,Ry] = Lx * Ly
... Ry Rx + [Rx,Ly] = Rx * Ry ... the Ri matrices of
the octonion regbirep ... will be used for the expression of Dirac
gamma-matrices. Ri-matrices ... are anticommuting antisymmetric
matrices forming the 64-dimensional Clifford algebra C6 with 6
generic elements ... The Ri matrices corresponding to different
multiplication tables are different. The transition between two
tables may be carried out by Li-matrices. ... The group SO(8), the
invariance group of the octonion norm, is the largest group which
can be related to the octonionic space with one dimension. The
exceptional groups F4, E6, E7, E8 are groups of various
geometries of the octonionic plane. ...".
Although Loops allow you to use a single nonassociative
octonion multiplication
product, they do not let you use a product (such as the Octonion
x-product and xy-product) that varies over an underlying
space, thus using the 480 octonion
multiplication products.
Loopoids
If you want to use a nonassociative
multiplication law that varies over an underlying manifold, thus
using the 480 octonion multiplication
products, you need to use a combination of Loop structure for
nonassociativity and Groupoid
structure for variation over an underlying space - something that
John Baez calls a Loopoid - which is defined as a groupoid
except that its composition law is alternative (not necessarily
associative).
The S7 loopoid structure that I like is an xy-product
groupoid with G = S7 and G0 = G = S7 and with a composition law that
takes into account the two points x and y in G0 = S7 of the two
arrows for w and z respectively, being defined as w o z = w oxy z,
thus producing a diagram like
S7 = G
| |
r| |s
| |
\/ \/
S7 = G0
/ \
\G2/
where the G2 loop is the autormorphism group of the octonions
implicit in the xy-product composition law
The S7 and S7 and G2 combine to form the
Lie Group Spin(8). Then you can look at the irreducible
representations of Spin(8) of dimensions
1 8 28 56 35
and their duals
35* 56* 28* 8* 1*
and combine them to form the 2^8 = 256-dimensional Clifford
Algebra Cl(8) with graded structure
1 8 28 56 (35+35*) 56* 28* 8* 1*
Then you can construct ANY Clifford algebra of the form Cl(8N) ,
and therefore, if you include subalgebras, ANY Clifford algebra, by
tensor product and periodicity factoring:
Cl(8N) = Cl(8) x ...(N-fold tensor product)... x Cl(8)
The net result of all this is, in my view, that
the 7-sphere S7
"naturally grows" to produce the Clifford algebra structure that I
use in my physics model (with signature
(1,7)).
As Geoffrey Dixon says in hep-th/9411063:
"... let e_a, a = 0, 1, ... , 7, be a basis for O ... the
Octonion algebra ... and ...
- W0 = {+/-e_a} [16 elements],
- W1 = ((+/-e_a +/-e_b)/sqrt(2) : a,b distinct [112
elements],
- W2 = ((+/-e_a +/-e_b +/-e_c +/-e_d)/2 : a,b,c,d distinct,
e_a(e_b(e_c e_d)) = +/-1} [224 elements],
- W3 = {(SUM^7_a=0 +/_e_a)/sqrt(8) : odd number of +'s},
a,b,c,d [in] {0, ... , 7} [128 elements]
...
The 240 elements of W0 u W2 are
the nearest neighbors (first shell) to the origin of an E8
lattice (so are the 240 elements of W1 u W3).
Define E8^h = Gh[W0 u W2], h = 1, ... , 7, where Gh is
the O(8) reflection taking e_0 <--> e_h.
These 7 sets are nearest neighbor points for 7 different E8
lattices ...[and they]... close under multiplication
...
Actually, E8^0 = W0 u W2 is not closed under the multiplication
we started with ... If, however we modify the product, using the
X-product ... then ... E8^0 is closed ...
there are 56 X-product variants of E8^7 (and by virtue of index
cycling, all the E8^h ... [thus producing 8x56 = 448
variants]) ...
we have an exact sequence
D4 in ZS3 --> E8^0 in S7 --> Z5 in S4
... where ... D4 ... is the [24-element] inner shell of
a ... D4 lattice ... [and] ... Z5 is
...the 5-dimensional cubic lattice
[with 32-element inner shell] ...".
I think that it might be interesting to write in loopoid formalism
the reflexive/recursive
equivalence between
- the 7 octonion imaginaries e_1, ... , e_7 and
- the 7 E8 lattices E8^1, ... , E8^7
7 Imaginary Octonions i j k E I J K
/ \
|
|
\ /
7 (Associative Triangles+1) x 16 (4 signs) = 112
/ \
/ / \ \
7 E8 Lattices | 224 + 16 = 240 Units
\ | / x2 (RL)
\ \ / / ||
\ / 480 Octonion Products
7 Coassociative Squares x 16 (4 signs) = 112
showing the expanding-nesting-Russian-doll structure of
point --> lattice -(pick a point)-> point --> lattice --> ...
and to compare that structure with
the Gray Code / Hilbert
Curve nesting-Russian-doll structure
... --> Cl(8x8x8) -(pick a 64)-> Cl(8x8) -(pick an 8)-> Cl(8)
of 3-dimensional Euclidean spacelike slices of 4-dimensional
physical spacetime that comes from the Clifford
Tensor Product Structure of the periodicity
of real Clifford algebras that is used in my physics model. That
structure is described on a
web page by William Gilbert:
"... We exhibit a direct generalization of Hilbert's
curve that fills a cube. The first three iterates of this curve
are shown.
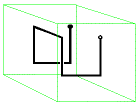
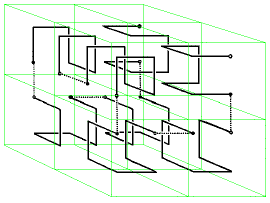
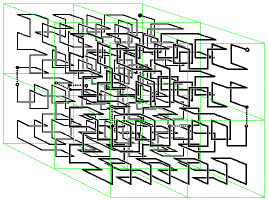
In constructing one iterate from the previous one, note that
the direction of the curve determines the orientation of the
smaller cubes inside the larger one.
The initial stage of this three dimensional curve can be
considered as coming from the 3-bit reflected Gray
code which traverses the 3-digit binary strings in such a way that
each string differs from its predecessor in a single position by
the addition or subtraction of 1. The kth iterate could be
considered a a generalized Gray code on
the Cartesian product set {0,1,2,...,2^k-1}^3.
The n-bit reflected binary Gray
code will describe a path on the edges of an n-dimensional cube
that can be used as the initial stage of a Hilbert curve that will
fill an n-dimensional cube. ...".
For a 4-dimensional physical Minkowski
spacetime neighborhood, add a 1-dimensional time to generalize
the 3-dimensional spatial structure described above to get a
structure with 16 vertices per 4-dimensional cell
... --> Cl(16x16x16) -(pick a 256)-> Cl(16x16) -(pick a 16)-> Cl(16) ->
-(pick an 8)-> Cl(8)
with the fundmental Cl(16) at each 4-dim vertex corresponding
by Cl(16) = Cl(8) x Cl(8) to 2 copies of Cl(8), aligned
along the time axis so that one is in the future of the other.
For a 6-dimensional physical
Conformal Spin(2,4) linear
spacetime neighborhood, add 2-dimensional time and 1-dimensional
space to generalize the 3-dimensional spatial structure described
above to get a structure with 64 vertices per 6-dimensional cell
... --> Cl(64x64x64) -(pick a 4,096)-> Cl(64x64) -(pick a 64)-> Cl(64) ->
-(pick an 8)-> Cl(8)
with the fundmental Cl(64) at each 6-dim vertex corresponding by
Cl(64) = Cl(8) x Cl(8) x Cl(8) x Cl(8) x Cl(8) x Cl(8) x Cl(8) x Cl(8)
to a configuration of 8 copies of Cl(8).
As Danny Ross Lunsford has noted, you can use the Traceless 4x4x2
- 2 = 30-real-dimensional Lie Algebra of SL(4,C) to construct a Lie
Algebra for a 6-dimensional linear spacetime. By imposing the
additional condition A* J = - J A where
0 0 0 1
0 0 1 0
J =
0 -1 0 0
-1 0 0 0
you get the 30/2 = 15-real-dimensional Lie Algebra of symplectic
(not-quaternionic-symplectic)
Sp(4,C) = Spin(3,3) = Spin(4,2) that corresponds to the Clifford
Algebra Cl(3,3) = Cl(4,2) = M(8,R) = Cl(0,6), which, as A. Sudbery
says in his paper Division algebras, (pseudo-) orthogonal groups and
spinors,J.Phys A, 17 (1984), 939-955 (see also math.RA/0203010),
leads to the usual 4x1 Dirac spinors and gamma-matrices.
Because I agree with John
Baez that fermions should be
quaternionic, I prefer (instead of taking SL(4,C)
as fundamental) to use the Conformal Lie Algebra of Spin(2,4)
with Clifford algebra Cl(2,4) = M(4,Q) =
Cl(1,5) = Cl(5,1) = Cl(6,0) which has 2x4 = 8-real-dimensional
half-spinors.
The octonion x-product
mentioned above is defined by Martin Cederwall and Christian
Preitschopf in hep-th/9309030
and described by Geoffrey Dixon in hep-th/9410202
where he says:
"... Let A,B,X [be in the octonions] O, with X a
unit octonion (X X* = 1) ... Define
A ox B = (A X)(X* B) = (A (B X)) X* = X ((X* A)
B)
the X-product of A and B. ... for fixed X, the algebra OX (O
endowed with the X-product) is isomorphic to O itself. Modulo sign
change each X gives rise to a distinct copy of O, so the orbit of
copies of O arising from any given starting copy is S7 / Z2 = RP7
, the manifold obtained from the 7-sphere by identifying opposite
points.
Moreover, composition of X-products is yet another X-product.
... there are 480 different
[octonion] multiplication tables ... these fall into
two groups of 240 ... related by the octonionic X-product.
...".
The octonion xy-product
is defined by Geoffrey Dixon in hep-th/9503053
where he says:
"... it is possible to modify the octonion product in
such a way that e_0 is not the identity of the result. In
particular, define
A oxy B = (AX)(Y*B) = A ox ((XY*) ox B) = (A oy (XY*)) oy
B ,
where as usual we assume that both X,Y [are in] S7
((the X-product is obtained by setting X+Y). Let OXY be O with
this modified product.
The question is, is this still isomorphic [to] O
itself? ... [yes] ... OXY [is isomorphic to] O.
...
The octonion X-product changes the octonion multiplication
table, but does not change the role of the identity. The
XY-product is very similar, but shifts the identity as well.
...
... the X-product ... generate[s] all the 480
renumberings of the e_a, a = 1, ..., 7 [imaginary octonion
basis elements], which leave e_0 = 1 fixed as the
identity.
There are 7680 renumberings of the entire collection, e_a, a =
0, ... , 7, and the XY product plays exactly the same role in this
context. ...
... in the X-product case the 480 renumberings arose from a
pair of octonion E8
lattices.
The XY-product renumberings are related in a similar fashion to
the pair of octonion /\16
lattices ...".
Note that
the /\16 Barnes-Wall lattice
(unimodular but odd) has 2x240 + 16x240 = 480 + 3,840 = 4,320 units,
related to the 16-dimensional Reed-Muller
code. The 7,680 octonion XY-product orbits are two sets of 3,840
units.
Further,
the variation of the octonion identity is equivalent to the action
on the identity of the automorphism group of the octonions, G2.
S7 and
NonAssociativity
R. M. Kane, in his book The Homology of Hopf Spaces (North-Holland
1988), says:
"... Stasheff's approach leads to the idea of an
obstruction theory for loop spaces. The A_n forms are a series of
intermediate stages between H-spaces (= A_2 spaces) and loop
spaces (= A_infinity spaces). ... in the homotopy category of
connected CW complexes we have the following identities:
loop spaces = topological groups = associative H-spaces =
A_infinity spaces ...
among the spheres, only S0, S1, S3, S7 possess A_2 forms
...[and so]... are H-spaces ... The
topological groups S0,S1, and S3 are...A_infinity spaces...= loop
space ...
[nonassociative octonionic] S7 ....[is a]...
H-space ... (= A_2 space) ...
S7 is not ... a A_3 space ...[which is] a homotopy
associative H-space...
S7_(3) is not homotopy associative ...[and]...
S7_(2) is not homotopy associative ... On the other hand,
S7_(p) is homotopy associative for p>= 5.
So the homotopy associativity obstruction is really mod 2 and
mod 3. ...".
Note that, even though S7 is a Moufang
loop, it is not a loop space in the sense used by Kane.
Kasper K. S. Andersen, Tilman Bauer, Jespar Grodal, and Erik Kjaer
Pedersen, in math.AT/0306234,
say:
"... Since the discovery of the
Hilton-Roitberg 'criminal' in 1968 it has been clear that not
every finite loop space is homotopy equivalent to a compact Lie
group. The conjecture emerged however, that this should hold
rationally ... In this paper we resolve this conjecture in the
negative by exhibiting a concrete finite loop space of rank 66
whose rational cohomology does not agree with that of any compact
Lie group. ...".
Since (in Kane's sense) loop space = topological group, their rank
66 loop space of dimension 1254 is an example of something that is a
topological group but not a Lie group.
Theorem 56 of Leon Pontrjagin's book Topological Groups (Princeton
1939) says:
"Let G be a compact topological group satisfying the
second axiom of countability. If G is locally connected ... and is
of finite dimension, it is a Lie group.".
The 1254-dimensional rank 66 loop space is a "connected finite
loop space", but it is only p-compact.
In a
post to the sci.physics.research thread Re: nonassociative category
and D-branes, John
Baez says:
"... a simple example ... of A_infinity categories ...
Take any topological space X. Take as objects the points of X, and
take as morphisms f: x -> y ... parametrized paths ... we can
compose them .. This composition is not associative!!! ...".
In a
1993 paper, Gregor Masbaum and Colin Roarke say:
"... A topological quantum field theory "TQFT" is a
functor from a "cobordism category" to a category of modules which
satisfies a number of properties ... Strictly speaking, a
cobordism category C is not a category in the usual sense. This is
because composition is not strictly associative nor are there
strict identities ... This is because (X u_S Y) u_T Z is not
strictly the same set as X u_S (Y u_T Z) where S [in] X,Y
and T [in] Y,Z are sets (though of course they are in
canonical bijection). Thus composition ... is only associative up
to canonical diffeomorphism. ... There is the question of whether
disjoint union can be defined in a coherent way in a cobordism
category ... The category of manifolds and diffeomorphisms is
certainly coherent and this might naively lead to the belief that
a cobordism category is also coherent ...
[ What is coherence? Noson S. Yanofsky in
math.CT/0007033
says "... The history of coherence theory has its roots in
homotopy theory. Saunders Mac Lane's foundational paper on
coherence theory was an abstraction of earlier work by James
Stasheff on H-spaces ..." and Peter Schauenburg in New
York J. Math. 7 (2001) 257-265 says "... It is well-known
that the tensor product of vector spaces is not associative on
the nose, but it is so up to isomorphism. ... MacLane's
coherence theorem ... says (... sloppily) that all diagrams one
can build up from associativity isomorphisms commute. ...".
]
... However this fails to work in detail for similar reasons to
the reason why a general cobordism category has non-associative
composition. ... Indeed the question of coherence is not really
meaningful for a category with non-associative composition so it
only really makes sense to ask whether our model categories can be
made coherent. But coherence must be by an isomorphism in the
category ... This is all very suggestive of an A_infinity
structure ... We conjecture that there is a genuine obstruction to
a cobordism category being strictly coherent ... and that there
may well be some interesting mathematical structure which can be
found by a careful investigation of the situation ...".
In hep-th/0102183,
C. I. Lazariou says:
"... there are good reasons (coming from the analysis of
the A-twisted topological string theory) to believe that A-type
D-branes in a type II compactification give a nonassociative
category (likely an A_infinity category), due to worldsheet
instanton effects. ...".
Tony Smith's Home Page ......


