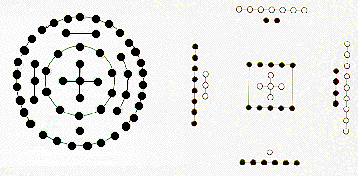
0 Tao, Simplex Physics
1 bit
2 superposition qbit
4 spacetime
16 fermions Ilm-al-Raml
256 Cl(8) IFA
65,536 Torah Genes
2^32 ~ 4 x 10^9 Genome Base Pairs
2^64 ~ 16 x 10^18 Brain Electrons Planck
2^128 ~ 256 x 10^36 Brain GraviPhotons Uncertainty
2^256 ~ 65,536 x 10^72 Particles in Universe
Chinese cosmology begins with the undivided Tai Chi,
then separating into Yin-Yang, ... :
Let o represent the undivided Tai Chi, a scalar point of origin:
| |
| |
_____|_____|_____
| |
| o |
_____|_____|_____
| |
| |
| |
Then add 4 vector directions of Physical Spacetime:
1, i, j, k of the quaternions
to get the 5 Elements:
| |
| i |
_____|_____|_____
| |
j | o | 1
_____|_____|_____
| |
| k |
| |
Then add 4 vector directions of Internal Symmetry Space:
E, I, J, K of the octonions,
which are the basis for the D4-D5-E6-E7 physics model,
to get 9 directions:
| |
J | i | I
_____|_____|_____
| |
j | o | 1
_____|_____|_____
| |
K | k | E
| |
The 10th direction is Yin-Yang reflection
of the 8 vector directions 1, i, j, k, E, I, J, K.
Now, identify the 3x3 square with the Magic Square
| |
4 | 9 | 2
_____|_____|_____
| |
3 | 5 | 7
_____|_____|_____
| |
8 | 1 | 6
| |
whose central number, 5, is also
central in the sequence 1,2,3,4, 5, 6,7,8,9
which sequence corresponds
to the octonions 1,i,j,k, 0, E,I,J,K
whose total number for each line is 15,
the dimension of the largest Hopf fibration
and the dimension of the imaginary sedenions.
If you take into account the direction in which you add each
of the 8 ways, and add all directed ways together
you get a total of 16x15 = 240
which is the number of vertices of a Witting polytope.
The total of all 9 numbers of the Magic Square is 45,
the dimension of the D5 Lie algebra Spin(10)
that is used in the D4-D5-E6-E7 physics model
in which
the D4 Spin(8) subgroup of Spin(10) corresponds
to 28 bivector gauge bosons
and the 16-dimensional homogeneous space
Spin(10) / Spin(8)xU(1)
corresponds to an 8-dimensional complex domain
whose Shilov boundary is RP1 x S7
corresponding to an 8-dimensional spacetime.
Perhaps about 5,300 years ago, China's first emperor, Fu Xi,
saw, rising from the Yellow River, a dragon-horse
with markings of the
shown here in its ancient and modern forms:
Fu Xi interpreted the 4 directions and 4 diagonal directions of the Ho Tu in terms of the Earlier Heaven arrangement of the 8 trigrams of the I Ching:
The 8 trigrams of the I Ching are similar to the 16 tetragrams of Ilm al-Raml (the Science of the Sands) attributed to the third Islamic prophet, Idris, which were preserved from the Global Early Civilization as the FA of the Fon people of Benin (Dahomey).
Baba Eyiogbe says "... It is indeed part of the Ifa tradition that Ifa was brought to China, but in a more limited form. This is sometimes attributed to a warrior path of Obatalá, Obatalá Ayaguna. This path of Obatalá is the Ifa diviner for the other paths of Obatalá as well (when Orunmila does not do it directly). ...".
It seems to me as though Vedic divination and Tai Shuan Ching are based on the Triality aspect of the 256-dimensional Cl(8) Clifford algebra of IFA, while I Ching is based on the 64-dimensional Cl(6) Clifford subalgebra of the Cl(8) of IFA.
When the 8 trigrams are combined in pairs according to the Fu Xi Earlier Heaven Ho Tu arrangement to make 64 hexagrams of the I Ching, you get a very symmetrical I Ching pattern
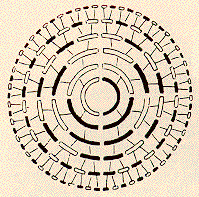
Although the Earlier Heaven arrangement of the 8 trigrams does not exactly correspond to the binary number sequence from 0 through 7 (it is 0,1,2,3,7,6,5,4 instead of 0,1,2,3,4,5,6,7), the Earlier Heaven arrangement of the 64 hexagrams does correspond to the binary number sequence from 0 through 63.
According to two 13 February 2001 articles in The New York Times by Nicholas Wade: "... Dr. J. Craig Venter and colleagues at Celera Genomics report in ...[ Science 291 (16 February 2001) 1304-1351 ]... that they have identified 26,588 human genes for sure, with another 12,731 candidate genes. ... Celera's rival, the publicly funded consortium of academic centers, has come to a similar conclusion. Its report in ...[ Nature 409 (15 February 2001) 860-921, where they say "... Genes (or at least their coding regions) comprise only a tiny fraction of human DNA, but they represent the major biological function of the genome and the main focus of interest by biologists. ...." ]... pegs the probable number of human genes at 30,000 to 40,000. Because the current gene-finding methods tend to overpredict, each side prefers the lower end of its range, and 30,000 seems to be the new favorite estimate. ... Most of the repetitive DNA sequences in the 75 percent of the genome that is essentially junk ceased to accumulate millions of years ago, but a few of sequences are still active and may do some good. The chromosomes themselves have a rich archaeology. Large blocks of genes seem to have been extensively copied from one human chromosome to another, beckoning genetic archaeologists to figure out the order in which the copying occurred and thus to reconstruct the history of the animal genome.
As the modest number of human genes became apparent, biologists in both teams were forced to think how to account for the greater complexity of people, given that they seem to possess only 50 percent more genes than the roundworm. It is not foolish pride to suppose there is something more to Homo sapiens than Caenorhabditis elegans. The roundworm is a little tube of a creature with a body of 959 cells, of which 302 are neurons in what passes for its brain. Humans have 100 trillion cells in their body, including 100 billion brain cells.
Several explanations are emerging for how to generate extra complexity other than by adding more genes. One is the general idea of combinatorial complexity - with just a few extra proteins one could make a much larger number of different combinations between them. ...
The two teams' first scanning of the genome suggests ... ways in which humans have become more complex than worms.
One comes from analysis of what are called protein domains. Proteins, the working parts of the cell, are often multipurpose tools, with each role being performed by a different section or domain of the protein. Many protein domains are very ancient. Comparing the domains of proteins made by the roundworm, the fruit fly and people, the consortium reports that only 7 percent of the protein domains found in people were absent from worm and fly, suggesting that "few new protein domains have been invented in the vertebrate lineage." But these domains have been mixed and matched in the vertebrate line to create more complex proteins. ...
Evolution has devised another ingenious way of increasing complexity, which is to divide a gene into several different segments and use them in different combinations to make different proteins. The protein-coding segments of a gene are known as exons and the DNA in between as introns. The initial transcript of a gene is processed by a delicate piece of cellular machinery known as a spliceosome, which strips out all the introns and joins the exons together. Sometimes, perhaps because of signals from the introns that have yet to be identified, certain exons are skipped, and a different protein is made. The ability to make different proteins from the same gene is known as alternative splicing. The consortium's biologists say that alternative splicing is more common in human cells than in the fly or worm and that the full set of human proteins could be five times as large as the worm's.
Another possible source of extra complexity is that human proteins have sugars and other chemical groups attached to them after synthesis.
There's a different explanation of human complexity, which is simply that the new low-ball figure of human genes derived by Celera and consortium is a gross undercount. Dr. William Haseltine, president of Human Genome Sciences, has long maintained that there are 120,000 or so human genes. ... Dr. Haseltine ... remains unshaken in his estimate of 100,000 to 120,000 genes. He said last week that his company had captured and sequenced 90,000 full-length genes, from which all alternative splice forms and other usual sources of confusion have been removed. He has made and tested the proteins from 10,000 of these genes. The consortium and Celera have both arrived at the same low number because both are using the same faulty methods, in his view. ... Dr. Haseltine notes that the gene-finding methods used by the two teams depend in part on looking for genes like those already known, a procedure that may well miss radically different types of genes. His own method, capturing the genes produced by variety of human cell types, is one that Dr. Venter says in his paper is the ultimate method of counting human genes. ... Dr. Eric S. Lander of the Whitehead Institute last week challenged Dr. Haseltine to make public all the genes he had found in a 1 percent region of the genome and let others assess his claim. ... Dr. Haseltine said yesterday that he was contemplating the best way to respond and that he was "planning to do so in one form or another, in the open literature."
Turning from genes to chromosomes, one of the most interesting discoveries in this week's papers concerns segmental duplications, or the copying of whole blocks of genes from one chromosome to the other. These block transfers are so extensive that they seem to have been a major evolutionary factor in the genome's present size and architecture. They may arise because of a protective mechanism in which the cell reinserts broken-off fragments of DNA back into the chromosomes.
In Celera's genome article, Dr. Venter presents a table showing how often blocks of similar genes in the same order can be found throughout the genome. Chromosome 19 seems the biggest borrower, or maybe lender, with blocks of genes shared with 16 other chromosomes. ... Segmental duplication is an important source of innovation because the copied block of genes is free to develop new functions. ...
Celera ordered the world's most powerful civilian computer to calculate how to assemble its
Its rival, the public consortium of academic centers, felt no need for a massive computer and assembly program because its genome decoding strategy didn't require one. But a computational biologist at the University of California, Santa Cruz, whose supervisor had been asked to help identify genes, realized the genome had to be assembled before gene identification could begin. In four weeks Jim Kent wrote an assembly program that put the consortium's jumble of DNA fragments into coherent order. It was this assembled sequence on which most of the consortium's genome analysis is based. Mr. Kent also wrote a browser, a program that aligns the known genes and other interpretive information in tracks above the actual genome sequence. Anyone wanting to take a tour of the human genome, with Mr. Kent's browser as their guide, can do so at genome.ucsc.edu. ...
One of the most intriguing hints that new biology may be discovered in the genome comes from an initial survey of the mouse genome, which Celera said this week it had assembled. Laying the mouse genome sequence over the human sequence is extremely revealing because most of the DNA has diverged in the 100 million years since mouse and man last shared a common ancestor. The DNA regions that are similar between the two species are those important enough to have been conserved. At a stroke, almost all the genes fall out as noticeably similar. So too do many of the control regions of DNA that precede the genes.
And Dr. Craig Venter, president of Celera, has now stated that there is a third category of similar DNA regions, which are not genes but are too extensive to be control regions. No one yet knows what the mystery regions are doing. ...".
According to a 21 January 2003 article in The New York Times by Andrew Pollack:
"... RNA and DNA are strings of chemical units called bases that embody the genetic code. The bases are represented by the letters A, C, G and either T in DNA or U in RNA. The C base always binds to G. A binds only to T or U. So a single strand of DNA or RNA can bind to another strand that has the complementary bases. Under what is known as the central dogma of genetics, genes, which are the recipes for making proteins, are part of the DNA of the chromosomes. When a protein is to be made, the DNA is copied onto a corresponding piece of single-stranded RNA, known as messenger RNA, that delivers the recipe to the cell's protein-making machinery. Proteins make up most of a cell and perform most of its functions, including turning genes on and off.But new evidence suggests that some RNA is not merely the intermediary between DNA and protein, but the end product. Some huge stretches of DNA that do not contain protein-coding genes and have been considered "junk" actually hold the code for some of this RNA. ...
... in addition to the DNA's containing the recipes for proteins, a lot more DNA was being copied into RNA. The recently deciphered mouse genome was found to have about twice as much in common with the human genome as could be accounted for by protein-coding genes. ... At least part of this overlap appears to be genes that produce RNA as their end product. What all of this RNA is doing is not clear ... But mounting evidence suggests that at least some RNA is involved in regulating the way genes are turned on or off. ... the most radical view: that RNA provides the command and control of cells. Proteins ... are like bricks and beams. But the RNA determines whether those bricks and beams become office buildings or houses. This RNA network ... provides the complexity that separates higher life forms from simpler ones. ...".
... Some genes ... produce tiny RNA's, known as micro-RNA's or miRNA, which are about 21 to 23 bases, or letters, in length. The micro-RNA's bind to matching pieces of messenger RNA, turn it into a double strand and keep it from doing its job. The process effectively stifles the production of the corresponding protein. ...
... RNA interference, or RNAi ...[occurs when]... double-strand RNA ... would silence the gene corresponding to that RNA. ...
... small interfering RNA's or siRNA's ...[are]... pieces of about 21 to 23 bases ... Each short segment attracts a phalanx of enzymes. Together, they seek out messenger RNA that corresponds to the small RNA and destroy it. ...
... micro-RNA's appear to be formed as longer stretches of RNA that fold back on themselves like hairpins to create double strands. The sequence of bases is sort of like a palindrome, so that when the folding occurs, complementary bases line up, and the two arms of the hairpin stick together. ...
... small RNA's bind to chromosomes to shut down genes more permanently than can be done by stifling messenger RNA. ...
... viruses ... sometimes create double-strand RNA when they replicate ... Mammalian cells, confronted with long double-strand RNA, basically destroy themselves as a defense against pathogens. But two years ago scientists at the Max Planck Institute found that short double-strand RNA, again about 21 to 23 bases, would not set off the self-destructive response but would silence the corresponding gene. ...".
According to a 7 July 2001 BBC article by Helen Briggs: "... Two rival teams that cracked the human genome may have underestimated the number of human genes, according to a new computer analysis. Scientists in the United States claim
nearly twice as many as the current consensus. ... a ... team, based at Ohio State University, Columbus, Ohio, has reanalysed the raw data, using a supercomputer, and come up with a higher estimate for the number of human genes. "We ended up with a higher estimated number of genes than the other two teams because we compared 13 different gene databases to the DNA sequences in the draft genome produced by the Human Genome Project," said Bo Yuan of Ohio State University. ... The discrepancy seems to arise from the process used to analyse human genetic data. ... The genome is the complete list of coded instructions needed to make a person There are 3.1 billion letters in the DNA code in every one of the 100 trillion cells in the human body If all of the DNA in the human body were put end to end, it would reach to the Sun and back more than 600 times. ... Buried within these coded instructions are the genes - 'sentences' which hold the instructions for the proteins of which human tissue is made. The genes occupy only about a hundredth of the length of the huge string of DNA, broken up into the 46 chromosomes in every cell. To fish out the genes, which are hidden among the long continuous string of letters, scientists rely on genetic databases. ... The Ohio State University team says Celera's genome map, and particularly, the Human Genome Project map relied mainly on two databases to locate the genes. They used these two databases plus 11 others. "We used more experimental evidence in assembling our map, and that suggests that there are probably between 65,000 and 75,000 transcriptional units," said Dr Yuan. A transcriptional unit is a length of DNA that shows strong evidence of being a gene but which requires future verification. This is where the dispute arises. "Some researchers are unsettled by the certainty with which the Human Genome Consortium is presenting its lower gene count," said Fred Wright of Ohio State University. "In my view, the final number of genes - when it is known - will lie somewhere between their high of 40,000 and our value of 70,000." ... Arguments over how many genes it takes to build a human being look set to continue. A gene sweepstake set up by scientists attending the Cold Spring Harbor Genome Meetings in the United States is still taking entries. To date, there have been 165 bets, ranging from 27,462 to 153,478 human genes. So far, the money is on 61,710. ...".
In cond-mat/0204078, Jimenez-Montano, Mora-Basanez, and Poschel say:
"... the genetic code may be represented by a six-dimensional boolean hypercubein which the codons (actually the code-words ...) occupy the [ 2^6 = 64 ] vertices (nodes) in such a way that all kinship neighborhoods are correctly represented. This approach is a particular application to binary sequences of length six of the general concept of sequence-space, first introduced in coding theory by Hamming ...
... The six-dimensional hypercube ...
... Each node is labeled with the corresponding amino acid ...
... It is well known in the field of Genetic Algorithms that a proper encoding is crucial to the success of an algorithm. Furthermore in ... R. A. Caruana and J. D. Schaffer, Representation and hidden bias: Gray vs. binary coding for genetic algorithms, in: J. Laird (ed.), Proceedings of the Fifth International Conference on Machine Learning, Morgan Kauffman Publ. Inc., 153-161 (San Mateo, 1988). ... it is shown the superiority of Gray coding over binary coding for the performance of a genetic algorithm. As it was shown above the structure of the genetic code is precisely the structure of a Gray code. ...".
Katya Walter has shown that the Fu Xi Earlier Heaven Ho Tu arrangement of the 64 hexagrams can represent the DNA genetic code:
Since the DNA genetic code can be represented by 4 things taken 3 at a time, or (2x2) x (2x2) x (2x2) = 64, and since the I Ching (which is based on 6 bars, each of which can be in 2 states - broken or unbroken) can be represented by 2 things taken 6 at a time, or 2 x 2 x 2 x 2 x 2 x 2 = 64, and since pairs of octonionic half-spinors of the Spin(0,8) Clifford algebra Cl(0,8) on which the D4-D5-E6-E7 physics model is based can be represented by 8 things taken 2 at a time, or (2x2x2) x (2x2x2) = 64, the genetic code, the I Ching, and the D4-D5-E6-E7 physics model are all just different representations of the same fundamental structure. The fundamental structure of 8 trigrams can not only be extended to 8x8 = 2^6 = 64 hexagrams, but also to 24-grams, of which there are 8^8 = 2^24 = 16,777,216. 24-grams are directly related to Golay codes and the Leech lattice. In that connection, the hexacode H6 is related to Golay codes and the Leech lattice. The hexacode H6 can be used to construct quantum-error-correcting codes that are based on GF(4), and an RNA code is based on 4 nucleotides UGAC, taken 3 at a time. Katya Walter has shown that the I Ching representation of the DNA genetic code can be transformed in a natural way to an I Ching representation of the RNA genetic code. The same fundamental structure is also shared by Penrose tilings and musical sequences. Further, you can represent genetic information by DNA sequence music (215k wav).
Katya Walter has shown that the representation of the DNA code by Fu Xi's Ho Tu arrangement of the I Ching is not superficial. The 55 points of the Ho Tu diagram can be divided into 27 SouthEast points and 28 NorthWest points, if the central point is put into the NorthWest part. The G-C base pair has 15 ring atoms and 12 other atoms, just as the SouthEast part has 15 even points and 12 odd points. The T-A base pair has 15 ring atoms and 13 other atoms, just as the NouthWest part has 15 even points and 13 odd points.
If the central point is allowed to remain central, and represent a U(1) propagator phase, then both the SouthEast and NorthWest parts have 15 even points and 12 odd points, so that they represent the 15 generators of the Spin(6) that gives conformal gravity and the Higgs mechanism and the 12 generators of the SU(3)xSU(2)xU(1) standard model, that is, all the gauge bosons of the D4-D5-E6-E7-E8 VoDou Physics model spacetime. Note that, to represent physical structures such as the DNA code and the D4-D5-E6-E7 model gauge bosons, the proper axis for the Ho Tu diagram is NorthEast-SouthWest, which is different from the North-South axis used to represent abstract Yin-Yang binary math structure. Such a diagonal axis will be used in the Lo Shu diagram, which is more oriented to representations of physical structures, as opposed to abstract structures.
China's third emperor Huang Di started the present Chinese calendar on 10 February 2697 BC. About 4,200 years ago, when Comet Hale-Bopp last appeared, Yu (father of the first emperor of the Xia dynasty) saw, rising from the Lo River, a turtle with markings of the
shown here in its ancient and modern forms:
Yu interpreted the 4 directions and 4 diagonal directions of the Lo Shu in terms of the Later Heaven arrangement of the 8 trigrams of the I Ching:
Note that the Yu Later Heaven Lo Shu arrangement of the 8 trigrams is not very symmetrical with respect to abstract Yin-Yang binary structure, but is very symmetrical with respect to a NorthEast-SouthWest axis and the physical representation of the 5 Elements. The NorthEast-SouthWest axis is Earth-Earth-Earth, SouthEast and East are Wood, NorthWest and West are Metal, and South is Fire and North is Water. Although the Lo Shu is not very symmetrical with respect to abstract Yin-Yang binary structure, the Lo Shu diagram does have the interesting mathematical structure of a Magic Square:
In addition to Square tilings of the plane,
there are Hexagonal tilings.
The only Magic Hexagon that exits also has central number 5:
15
14 13
9 8 10
6 4
11 5 12
1 2
18 7 16
17 19
3
There are 15 sums, 5 parallel to each of its 3 axes.
Each sum is 38 = 2x19, and there are 1+6+12 = 19 cells.
19x19 is the dimension of the lattice of a WeiQi board.
Perhaps because of its lack of abstract Yin-Yang binary symmetry,
the Later Heaven Lo Shu arrangement of the 8 trigrams
did not lead Yu to make
a corresponding arrangement of the 64 hexagrams.
It was not until about 3,100 years ago
that Wen-wang (father of the founder of the Zhou dynasty)
made a Lo Shu arrangement of the 64 hexagrams.
Since Wen-wang's son Wu-wang named him (posthumously) as the first emperor of the Zhou dynasty, Wen-wang is known as King Wen, and his arrangement of the 64 hexagrams often called the King Wen arrangement. King Wen created his arrangement while imprisoned by the Shang emperor. It was not an arrangement to describe abstract principles, but to describe his life and how it could be useful in overthrowing the corrupt Shang emperor and setting up a better government. The 64 King Wen hexagrams are arranged in 32 dual pairs. For 28 of the pairs, one is the other turned upside down. 8 hexagrams are the same turned upside down, so they make up 4 pairs of opposites. The 28 upside-down symmetric pairs have a similar symmetry to the 28-dimensional antisymmetric real 8x8 matrices that represent Spin(0,8) of the D4-D5-E6-E7 physics model. King Wen's arrangement is designed for life in our physical world, beginning with pure Yang, forward moving Heaven, and ending with a hexagram described by two characters that mean "not yet across (a river)", so that its ending is really also a beginning, just as in real life. Perhaps that is why the King Wen arrangement is the one most often seen in present-day I Ching books. Another son of King Wen was the Duke of Zhou, the brother of King Wu (Wu-wang). When King Wen wrote about the 64 hexagrams, he wrote for each entire hexagram a Judgment. The Duke of Zhou wrote a poetic text, the Line Text, for each hexagram Judgment. Each poem line corresponds to a hexagram line, and each whole poem goes with the Chinese characters for each hexagram Judgment. Much later commentaries, such as the Ten Wings, have been added to the present-day I Ching books. My opinion about such later commentaries is the same as that of Rosemary and Kerson Huang: "The poetic aspect of the I Ching, however, has been obscured by the Ten Wings. How can you enjoy poetry if every line is followed by government regulations on how to read it?"
Of course, it is possible to make other arrangements of the 8 trigrams and 64 hexagrams of the

than the Fu Xi and King Wen arrangements. The 8 trigrams can be arranged in 8! = 40,320 different orders. As well as ordering the 8 trigrams differently, you can pick subsets of the 8 trigrams. That can also be done in many ways: there are 2^8 = 256 subsets of the 8 trigrams. The number of subsets of the 8 trigrams is the dimension of the Cl(0,8) Clifford algebra that is used in the D4-D5-E6-E7 physics model and is related to ordering the 8 trigrams by the Clifford sequence corresponding to the binary numbers from 0 through 7 You can arrange the 64 hexagrams in 64! (about 1.27 x 10^89) different orders. As well as ordering the 64 hexagrams differently, you can pick subsets of the 64 hexagrams. That can also be done in many ways: there are 2^64 (about 1.844 x 10^19) subsets of the 64 hexagrams. The number of subsets of the 64 hexagrams is useful in estimating the Planck mass. If you want more possibilities, consider the (2^64)! possible orderings of all 2^64 subsets of the 64 hexagrams. If you want still more, consider the possible orderings within each of the 2^64 subsets of the 64 hexagrams. The ordering of the 64 hexagrams in the HuangLao Daoist Mawangdui Silk Text may be related to historical events of the time period from 613 BC (Emperor Zhuang of Chu) to the time the manuscript was copied, probably about 202-195 BC (Emperor Liu Bang of Han). A natural ordering of the 64 hexagrams is the I Ching lattice of Billy Culver
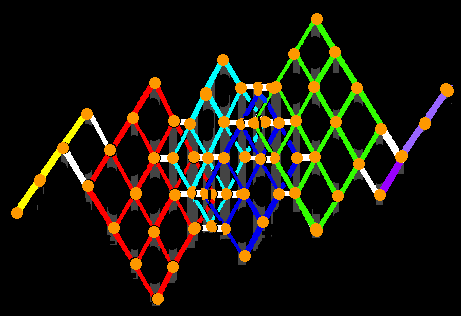
in which the 64 hexagrams are in groups of
4 + 16 + (12+12) + 16 + 4 = 4 + 16 + 24 + 16 + 4 = 64
This can be seen as a 4-fold expansion of the
1 4 6 4 1
level of the Su Meru triangle.
Another order is based on the 1 6 15 20 15 6 1 level, with 2^6 = 64 elements, of the Su Meru triangle:
----------------------
0 1 hexagram with 0 - -
----------------------
1 2 4 8 16 32 6 hexagrams with 1 - -
----------------------
3 6 12 24 48
5 10 20 40
9 18 36 15 hexagrams with 2 - -
17 34
33
----------------------
7 14 28
11 22
13 26
19
21
25
====================== 10+10 = 20 hexagrams with 3 - -
38 = 63 - 25
42 = 63 - 21
44 = 63 - 19
37 50 = 63 - 13
41 52 = 63 - 11
35 49 56 = 63 - 7
----------------------
30 = 63 - 33
29 46 = 63 - 17
27 45 54 = 63 - 9 15 hexagrams with 4 - -
23 43 53 58 = 63 - 5
15 39 51 57 60 = 63 - 3
----------------------
31 47 55 59 61 62 = 63 - 1 6 hexagrams with 5 - -
----------------------
63 = 63 - 0 1 hexagram with 6 - -
----------------------
Still another interesting order for the hexagrams
uses the order of this 8x8 Magic Square whose sum is 260.
It is constructed by writing the numbers 1...64 in sequence
and then reversing the order of the green entries:
64 2 3 61 60 6 7 8
9 55 54 12 13 51 50 16
17 47 46 20 21 43 42 24
40 26 27 37 36 30 31 32
32 34 35 29 28 38 39 25
41 23 22 44 45 19 18 48
49 15 14 52 53 11 10 56
8 58 59 5 4 62 63 1
Since 8x8 = 64 = 4x4x4 is both a square and a cube
(the smallest such number greater than 1)
you can use the same numbers and a similar method
to construct a 4x4x4 Magic Cube with sum 130.
Here is such a cube as constructed by Meredith Houlton:
1 63 62 4
60 6 7 57
56 10 11 53
13 51 50 16
48 18 19 45
21 43 42 24
25 39 38 28
36 30 31 33
32 34 35 29
37 27 26 40
41 23 22 44
20 46 47 17
49 15 14 52
12 54 55 9
8 58 59 5
61 3 2 64
The sum of the 8x8 Magic Square, 260,
is twice the sum (130) of the 4x4x4 Magic Cube.
The Maya calendar uses a period of 260 days, the Tzolkin,
as well as a period of 365 days, the Haab.
A version of the
was written by Yang Hsiung, who lived from about 53 BC to about 18 AD. As the I Ching is based on hexagrams of binary lines, for a total of 2x2x2x2x2x2 = 8x8 = 64 hexagrams, the Tai Hsuan Ching is based on tetragrams of ternary lines, for a total of 3x3x3x3 = 9x9 = 81 tetragrams.
It seems to me as though Vedic divination and Tai Shuan Ching are based on the Triality aspect of the 256-dimensional Cl(8) Clifford algebra of IFA, while I Ching is based on the 64-dimensional Cl(6) Clifford subalgebra of the Cl(8) of IFA.
The progression from the I Ching to the Tai Hsuan Ching is similar to a number of things:
The numbers shown in the arrangement below are the ternary numbers plus 1, as the ternary numbers go from 0 to 80 instead of from 1 to 81.
The ternary number arrangement is similar to
the Fu Xi binary number arrangement of the I Ching.
The 81 tetragrams correspond to the 81 verses
of the Tao Te Ching.
The Tai Hsuan Ching may be at least as
old as the King Wen arrangement of the I Ching,
since such tetragrams have been
found on Shang and Zhou dynasty oracle bones.
To construct the Tai Hsuan Ching,
start with the 3x3 I Ching Magic Square
| |
4 | 9 | 2
_____|_____|_____
| |
3 | 5 | 7
_____|_____|_____
| |
8 | 1 | 6
| |
whose central number, 5, is also
central in the sequence 1,2,3,4, 5, 6,7,8,9
which sequence corresponds
to the octonions 1,i,j,k, 0, E,I,J,K
whose total number for each line is 15,
the dimension of the largest Hopf fibration
and the dimension of the imaginary sedenions.
If you take into account the direction in which you add each
of the 8 ways, and add all directed ways together
you get a total of 16x15 = 240
which is the number of vertices of a Witting polytope.
The total of all 9 numbers is 45,
the dimension of the D5 Lie algebra Spin(10)
that is used in the D4-D5-E6-E7 physics model
in which
the D4 Spin(8) subgroup of Spin(10) corresponds
to 28 bivector gauge bosons
and the 16-dimensional homogeneous space
Spin(10) / Spin(8)xU(1)
corresponds to an 8-dimensional complex domain
whose Shilov boundary is RP1 x S7
corresponding to an 8-dimensional spacetime.
Notice that the 3x3 Magic Square gives
the gauge bosons and the spacetime
of the D4-D5-E6-E7 physics model
but
does not contain the spinor fermions.
The 3 generations of spinor fermions
corresond to a Lie Algebra Magic Square.
The Tai Hsuan Ching construction will
give us the spinor fermions,
and therefore corresponds to
the complete D4-D5-E6-E7 physics model.
To construct the Tai Hsaun Ching,
consider the Magic Square sequence as a line
3 8 4 9 5 1 6 2 7
with central 5 and opposite pairs at equal distances.
If you try to make that, or a multiple of it,
into a 9x9 Magic Square whose central number
is the central number 41 of 9x9 = 81 = 40+1+40,
you will fail because 41 is not a multiple of 5.
However, since 365 = 5x73 is
the central number of 729 = 364+1+364 , you can
make a 9x9x9 Magic Cube with 9x9x9 = 729 entries,
each 9x9 square of which is a Magic Square.
The Magic Cube of the Tai Hsaun Ching
gives the same sum for all lines parallel to an edge,
and for all diagonals containing the central entry.
The central number of the Magic Cube, 365,
the period of a Maya Haab.
The total number for each line is 3,285 = 219 x 15.
The total of all numbers is 266,085 = 5,913 x 45.
Since 729 is the smallest odd number greater than 1
that is both a cubic number and a square number,
the 729 entries of the 9x9x9 Magic Cube with central entry 365
can be rearranged to form
a 27x27 Magic Square with 729 entries and central entry 365.
27 = 3x3x3 = 13+1+13 is a cubic number with central number 14,
and there is a 3x3x3 Magic Cube with central entry 14
(14 is the dimension of the exceptional Lie algebra G2)
and sum 42:
10 24 8 26 1 15 6 17 19
23 7 12 3 14 25 16 21 5
9 11 22 13 27 2 20 4 18
The lowest dimensional non-trivial representation
of the Lie algebra E6 is 27-dimensional,
corresponding to the 27-dimensional Jordan algebra
of 3x3 Hermitian octonionic matrices.
E6 is the 78-dimensional Lie algebra
that is used in the D4-D5-E6-E7 physics model
in which
the 32-dimensional homogeneous space
E6 / Spin(10)xU(1)
corresponds to a 16-dimensional complex domain
whose Shilov boundary is two copies of RP1 x S7
corresponding to Spin(8) spinors, representing
8 fermion particles and 8 fermion antiparticles.
All 4 components of the D4-D5-E6-E7 model,
arising from the 4 fundamental representations of Spin(8),
are contained within E6:
8 half-spinor fermion particles;
8 half-spinor fermion antiparticles;
8-dimensional spacetime
(4 Physical Spacetime dimensions and
4 Internal Symmetry dimensions);
and 28 gauge bosons
(12 for the Standard Model,
15 for Conformal Gravity and the Higgs Mechanism, and
1 for propagator phase).
The Lie algebra E6 is 72+6 = 78-dimensional,
and has Weyl group of order 72x6! = 51,840
which is the symmetry group of the 6-dimensional polytope 2_21
with 27 vertices and 27+72 faces
which is also the symmetry group of the 27 line configuration:
The 78 dimensions of E6 correspond to the 78 Tarot cards. Since E6 as used in the D4-D5-E6-E7 physics model represents the two half-spinor representations of Spin(8),
For Spin(n) up to n = 8, here are is their Clifford algebra structure as shown by the Yang Hui (Pascal) triangle and the dimensions of their spinor representations
n Total Spinor Dimension Dimension 0 1 2^0 = 1= 1x1 1 1 1 1 2^1 = 2= 1+1 1 2 1 2 1 2^2 = 4= 2x2 2 = 1+1 3 1 3 3 1 2^3 = 8= 4+4 2 4 1 4 6 4 1 2^4 = 16= 4x4 4 = 2+2 5 1 5 10 10 5 1 2^5 = 32=16+16 4 6 1 6 15 20 15 6 1 2^6 = 64= 8x8 8 = 4+4 7 1 7 21 35 35 21 7 1 2^7 = 128=64+64 8 8 1 8 28 56 70 56 28 8 1 2^8 = 256=16x16 16 = 8+8
Since each row of the Yang Hui (Pascal) triangle corresponds to the graded structure of an exterior algebra with a wedge product, call each row a wedge string. In this pattern, the 28 and the 8 for n = 8 correspond to the 28 gauge bosons of the D4 Lie algebra and to the 8 spacetime (4 physical and 4 internal symmetry) dimensions that are added when you go to the D5 Lie algebra. The 8+8 = 16 fermions that are added when you go to E6, corresponding to spinors, do not correspond to any single grade of the n = 8 Clifford algebra with graded structure 1 8 28 56 70 56 28 8 1 but correspond to the entire Clifford algebra as a whole. The total dimension of the Clifford algebra is given by the Yang Hui (Pascal) triangle pattern of binary expansion (1 + 1)^n, which corresponds to the number of vertices of a hypercube of dimension n. The spinors of the Clifford algebra of dimension n are derived from the total matrix algebra of dimension 2^n with pattern n 0 1 1 2 2 4 3 8 4 16 5 32 6 64 7 128 8 256 This can be expanded to a pattern n 0 1 1 2 1 2 4 2 1 3 8 4 2 1 4 16 8 4 2 1 5 32 16 8 4 2 1 6 64 32 16 8 4 2 1 7 128 64 32 16 8 4 2 1 8 256 128 64 32 16 8 4 2 1 in the same form as the Yang Hui (Pascal) triangle. Call each row a spinor string. For a given row in the binary (1+1)^n Yang Hui (Pascal) triangle the string product of a spinor string and a wedge string (2^N, 2^(N-1), 2^(N-2), ... , 2^(N-J), ... , 4, 2, 1) (1 , N , N(N-1)/2,...,N^k J^(N-k)/(k!(N-k)!)J),...,N(N-1)/2,N,1) gives the rows of the ternary (1+2)^n power of 3 triangle n 0 1 3^0 = 1 1 2 1 3^1 = 3 2 4 4 1 3^2 = 9 3 8 12 6 1 3^3 = 27 4 16 32 24 8 1 3^4 = 81 5 32 80 80 40 10 1 3^5 = 243 6 64 192 240 160 60 12 1 3^6 = 729 7 128 448 672 560 280 84 14 1 3^7 = 2,187 8 256 1024 1792 1792 1120 448 112 16 1 3^8 = 6,561 Just as the binary (1+1)^n triangle corresponds to the I Ching, the ternary (1+2)^n triangle corresponds to the Tai Hsuan Ching. The ternary triangle also describes the sub-hypercube structure of a hypercube. The ternary power of 3 triangle is not only used in representations of the spinors in the D4-D5-E6-E7 model, it was also by Plato in describing cosmogony and music.
has central entry 365, and 365 = 73 x 5 is the whole number of days in a solar year. The corresponding Maya 365-day period is called the Haab. The 8x8 Magic Square and 4x4x4 Magic Cube of the I Ching have sums 260 and 130 = 260/2, and 260 = 13 x 5 x 4 is the number of days in a Maya Tzolkin. The common period of the Maya Haab and Tzolkin is 73 x 5 x 13 x 4 = 18,980 days or 52 Haab. The synodic period of Venus is 584 = 73 x 8. The common period of the Maya Haab and the synodic period of Venus is 73 x 5 x 8 = 37,960 days or 104 Haab. The common period of the Maya Haab and Tzolkin and the synodic period of Venus is 73 x 5 x 8 = 2,929 days or 8 Haab. Since the 8x8 = 4x4x4 = 64, and 584 = 2 x 260 + 64. the synodic period of Venus is naturally expressible in terms of the 8x8 Magic Square and the 4x4x4 Magic Cube. Here is the 9x9x9 Magic Cube:
543 179 616 252 689 397 33 470 106 107 544 180 617 244 690 398 34 471 472 108 545 172 618 245 691 399 35 36 473 100 546 173 619 246 692 400 401 28 474 101 547 174 620 247 693 685 402 29 475 102 548 175 621 248 249 686 403 30 476 103 549 176 613 614 250 687 404 31 477 104 541 177 178 615 251 688 405 32 469 105 542
97 534 170 607 324 680 388 24 461 462 98 535 171 608 316 681 389 25 26 463 99 536 163 609 317 682 390 391 27 464 91 537 164 610 318 683 684 392 19 465 92 538 165 611 319 320 676 393 20 466 93 539 166 612 604 321 677 394 21 467 94 540 167 168 605 322 678 395 22 468 95 532 533 169 606 323 679 396 23 460 96
452 88 525 242 598 315 671 379 15 16 453 89 526 243 599 307 672 380 381 17 454 90 527 235 600 308 673 674 382 18 455 82 528 236 601 309 310 675 383 10 456 83 529 237 602 603 311 667 384 11 457 84 530 238 239 595 312 668 385 12 458 85 531 523 240 596 313 669 386 13 459 86 87 524 241 597 314 670 387 14 451
4 Thanks to Jeff Knox for correcting my error in row 1, col 5, where I had written 231 by mistake.
6 443 160 516 233 589 306 662 370 371 7 444 161 517 234 590 298 663 664 372 8 445 162 518 226 591 299 300 665 373 9 446 154 519 227 592 593 301 666 374 1 447 155 520 228 229 594 302 658 375 2 448 156 521 522 230 586 303 659 376 3 449 157 158 514 231 587 304 660 377 4 450 442 159 515 232 588 305 661 378 5
361 78 434 151 507 224 580 297 653 654 362 79 435 152 508 225 581 289 290 655 363 80 436 153 509 217 582 583 291 656 364 81 437 145 510 218 219 584 292 657 365 73 438 146 511 512 220 585 293 649 366 74 439 147 148 513 221 577 294 650 367 75 440 441 149 505 222 578 295 651 368 76 77 433 150 506 223 579 296 652 369
725 352 69 425 142 498 215 571 288 280 726 353 70 426 143 499 216 572 573 281 727 354 71 427 144 500 208 209 574 282 728 355 72 428 136 501 502 210 575 283 729 356 64 429 137 138 503 211 576 284 721 357 65 430 431 139 504 212 568 285 722 358 66 67 432 140 496 213 569 286 723 359 360 68 424 141 497 214 570 287 724
279 716 343 60 416 133 489 206 643 644 271 717 344 61 417 134 490 207 199 645 272 718 345 62 418 135 491 492 200 646 273 719 346 63 419 127 128 493 201 647 274 720 347 55 420 421 129 494 202 648 275 712 348 56 57 422 130 495 203 640 276 713 349 150 58 423 131 487 204 641 277 714 715 351 59 415 132 488 205 642 278
634 270 707 334 51 407 124 561 197 198 635 262 708 335 52 408 125 562 563 190 636 263 709 336 53 409 126 118 564 191 637 264 710 337 54 410 411 119 565 192 638 265 711 338 46 47 412 120 566 193 639 266 703 339 340 48 413 121 567 194 631 267 704 705 341 49 414 122 559 195 632 268 269 706 342 50 406 123 560 196 633
188 625 261 698 325 42 479 115 552 553 189 626 253 699 326 43 480 116 117 554 181 627 254 700 327 44 481 482 109 555 182 628 255 701 328 45 37 483 110 556 183 629 256 702 329 330 38 484 111 557 184 630 257 694 695 331 39 485 112 558 185 622 258 259 696 332 40 486 113 550 186 623 624 260 697 333 41 478 114 551 187
Andrews, W. S., Magic Squares and Cubes (Dover 1960). Arguelles, Jose, Earth Ascending (3rd ed) (Bear 1996). (Jose Arguelles noticed similar correspondencies between 8x8 Magic Squares, the I Ching, and the Mayan calendar, at least as early as the first edition of Earth Ascending in 1984.) Coxeter, H. S. M., Math. Z. 200 (1988) 3-45. Huang, Kerson and Rosemary, I Ching (Workman 1987). Lau, Kwan, Feng Shui for Today (Tengu 1996). Nylan, Michael, The Canon of Supreme Mystery by Yan Hsiung, A Translation with Commentary of the T'ai hsuan ching (State University of New York Press 1993 - A popular version is entitled The Elemental Changes (Roger Clough has a web page with some notations of errata, such as typos etc.) Schele, Linda and Freidel, David, A Forest of Kings (Quill, William Morrow 1990). Shaughnessy, Edward, I Ching (Ballantine 1996). Walter, Katya, Tao of Chaos (Element 1994). Walters, Derek, Chinese Astrology (Aquarian 1992). Walters, Derek, The Alternative I Ching (Aquarian Press 1987), originally published in 1983 under the title The Tai Hsuan Ching. Wells, David, The Penguin Dictionary of Curious and Interesting Numbers (Penguin 1986). Williams, C. A. S., Chinese Symbolism and Art Motifs (Tuttle 1974). Wong, Eva, Feng Shui (Shambhala 1996). Wong, Eva, Taoism (Shambhala 1997). Yates, Robin D. S., Five Lost Classics: Tao, Huang-Lao, and Yin-Yang in Han China (Ballantine Books 1997).
The I Ching web site of Chris Lofting, which has a lot of very interesting philosophical discussion.
The I Ching web site of Christopher Garrity, which relates the 8x8 I Ching Matrix to a Matrix of the 8 Colors of the SU(3) Color Force: white; red, blue, and green; and their complementary colors.
The T'ai Hsuan Ching website of Roger Clough has a lot of interesting information about the Tai Hsuan Ching.
Michael Nylan and Nathan Sivin have a web page with their 1987 (revised 1995) article entitled The First Neo-Confucianism An Introduction to Yang Hsiung's "Canon Of Supreme Mystery" (T'ai Hsuan Ching, Ca. 4 B.C.).
Tony Smith's Home Page ......