E8 Physics
Model and 26D String Theory
Frank Dodd (Tony) Smith, Jr. - 2012
A
physically realistic Lattice Bosonic String Theory with Strings =
World-Lines
and Monster Group Symmetry
containing gravity
and the Standard Model
can be
constructed consistently with the E8 physics model
248-dim E8
= 120-dim adjoint D8 + 128-dim half-spinor D8
= (28 + 28 + 64) + (64 + 64)
Joseph
Polchinski, in
his books String Theory vols. I and II( Cambridge
1998), says:
"... the closed ... unoriented ... bosonic string ... theory has
the maximal
26-dimensional Poincare invariance ... It is possible to have a
consistent
theory ...[with]... the dilaton ...
the [string-]graviton ...[and]... the tachyon
...[whose]... negative mass-squared means that the no-string 'vacuum'
is
actually unstable ... ".
The dilaton
of E8 Physics sets the Planck scale as the scale for
the 16
dimensions
that are orbifolded fermion particles and anti-particles
and the 4
dimensions of the CP2 Internal Symmetry Space of M4xCP2 spacetime.
The remaining
26-16-4 = 6 dimensions are the
Conformal Physical Spacetime with Spin(2,4)
= SU(2,2)
symmetry that produces M4 Physical Spacetime.
The string-graviton
of E8 Physics is a spin-2 interaction
among strings.
If Strings =
World Lines and World Lines are
past and future histories of particles,
then
string-graviton interactions determine a Cramer Transaction Quantum
Theory
discussed
in quantum-ph/0408109. Roger Penrose in "Road to Reality" (Knopf
2004) says: "... quantum
mechanics ... alternates between ... unitary
evolution U ... and state reduction
R ... quantum state reduction ... is
... objective ... OR ...
it is always a
gravitational phenomenon ... [A] conscious event ... would be ...
orchestrated
OR ... of ... large-scale quantum coherence ... of ... microtubules
...".
String-Gravity
produces
Sarfatti-Bohm
Quantum
Potential
with
Back-Reaction.
It is
distinct from the MacDowell-Mansouri
Gravity of stars and
planets.
The tachyon
produces the instability of a truly empty vacuum state with no strings.
It is
natural, because if our Universe were ever
to be in a state with no strings,
then tachyons
would
create strings = World Lines thus filling our Universe with the
particles and
World-Lines = strings that we see. Something like this is necessary for
particle creation in the Inflationary Era of non-unitary Octonionic
processes.
Our
construction of a 26D String Theory
consistent with E8 Physics uses a structure that is not well-known,
so I will mention it here before we start:
There are 7
independent E8 lattices, each corresponding to one of the 7 imaginary
octionions denoted by iE8, jE8, kE8, EE8, IE8, JE8, and KE8 and related
to both D8 adjoint and half-spinor parts of E8 and with 240 first-shell
vertices. An 8th E8 lattice 1E8 with 240 first-shell vertices related
to the D8 adjoint part of E8 is related to the 7 octonion imaginary
lattices (viXra 1301.0150v2) .
It can act as an effectively independent lattice as part of the basis
subsets
{1E8,EE8} or
{1E8,iE8,jE8,kE8}.
With that in
mind,
here is the construction:
Step 1:
Consider the
26
Dimensions of Bosonic String Theory as the 26-dimensional traceless
part J3(O)o
a
O+
Ov
O+*
b O-
Ov*
O-* -a-b
(where
Ov, O+, and O- are in Octonion space with basis {1,i,j,k,E,I,J,K} and a
and b
are real numbers with basis {1})
of
the 27-dimensional Jordan algebra J3(O) of 3x3 Hermitian Octonion
matrices.
Step 2:
Take a D3
brane to
correspond to the Imaginary Quaternionic associative subspace spanned
by {i,j,k} in the 8-dimenisonal Octonionic
Ov space.
Step 3:
Compactify
the
4-dimensional co-associative subspace spanned by {E,I,J,K}
in
the
Octonionic
Ov
space
as
a CP2 = SU(3)/U(2), with its 4 world-brane
scalars corresponding to the 4 covariant components of a Higgs scalar.
Add this
subspace to
D3, to get D7.
Step 4:
Orbifold the
1-dimensional Real subspace spanned by {1} in the Octonionic Ov space
by the
discrete multiplicative group Z2 = {-1,+1},
with its
fixed points {-1,+1} corresponding to past and future time. This
discretizes
time steps and gets rid of the world-brane scalar corresponding to the
subspace
spanned by {1} in Ov. It also gives our brane a 2-level timelike
structure, so
that its past can connect to the future of a preceding brane and its
future can
connect to the past of a succeeding brane.
Add this
subspace to
D7, to get D8.
D8, our basic
Brane,
looks like two layers (past and future) of D7s.
Beyond D8 our
String
Theory has 26 - 8 = 18 dimensions, of which 25 - 8 have corresponding
world-brane scalars:
¥
8 world-brane
scalars for Octonionic O+
space;
¥
8 world-brane
scalars for Octonionic O-
space;
¥
1 world-brane
scalars for real a space;
and
¥
1 dimension,
for real b space, in which
the D8 branes containing spacelike D3s are stacked in timelike order.
Step 5:
To get rid of
the
world-brane scalars corresponding to the Octonionic O+ space, orbifold
it by
the 16-element discrete multiplicative group Oct16 = {+/-1,+/-i,+/-j,+/-k,+/-E,+/-I,+/-J,+/-K}
to reduce O+ to 16 singular points
{-1,-i,-j,-k,-E,-I,-J,-K,+1,+i,+j,+k,+E,+I,+J,+K}.
¥
Let the 8 O+
singular points {-1,-i,-j,-k,-E,-I,-J,-K}
correspond to the fundamental fermion
particles {neutrino, red up quark, green up quark, blue up quark,
electron, red
down quark, green down quark, blue down quark} located on the past D7
layer of
D8.
¥
Let the 8 O+
singular points {+1,+i,+j,+k,+E,+I,+J,+K}
correspond to the fundamental fermion
particles {neutrino, red up quark, green up quark, blue up quark,
electron, red
down quark, green down quark, blue down quark} located on the future D7
layer
of D8.
The 8
components of
the 8 fundamental first-generation fermion particles = 8x8 = 64
correspond to
the 64 of the
128-dim half-spinor D8 part of
E8.
This gets rid
of the 8
world-brane scalars corresponding to O+, and leaves:
¥
8 world-brane
scalars for Octonionic O-
space;
¥
1 world-brane
scalars for real a space;
and
¥
1 dimension,
for real b space, in which
the D8 branes containing spacelike D3s are stacked in timelike order.
Step 6:
To get rid of
the
world-brane scalars corresponding to the Octonionic O- space, orbifold
it by
the 16-element discrete multiplicative group Oct16 = {+/-1,+/-i,+/-j,+/-k,+/-E,+/-I,+/-J,+/-K}
to reduce O- to 16 singular points
{-1,-i,-j,-k,-E,-I,-J,-K,+1,+i,+j,+k,+E,+I,+J,+K}.
¥
Let the 8 O-
singular points {-1,-i,-j,-k,-E,-I,-J,-K}
correspond to the fundamental fermion
anti-particles {anti-neutrino, red up anti-quark, green up anti-quark,
blue up
anti-quark, positron, red down anti-quark, green down anti-quark, blue
down
anti-quark} located on the past D7 layer of D8.
¥
Let the 8 O-
singular points {+1,+i,+j,+k,+E,+I,+J,+K}
correspond to the fundamental fermion
anti-particles {anti-neutrino, red up anti-quark, green up anti-quark,
blue up
anti-quark, positron, red down anti-quark, green down anti-quark, blue
down
anti-quark} located on the future D7 layer of D8.
The 8
components of
the 8 fundamental first-generation fermion anti-particles = 8x8 = 64
correspond
to the 64 of the
128-dim
half-spinor D8 part of E8.
This gets rid
of the 8
world-brane scalars corresponding to O-, and leaves:
¥
1 world-brane
scalars for real a space;
and
¥
1 dimension,
for real b space, in which
the D8 branes containing spacelike D3s are stacked in timelike order.
Step 7:
Let the 1
world-brane
scalar for real a space correspond to a Bohm-type
Quantum
Potential
acting
on
strings
in
the stack of D8 branes.
Interpret
strings as world-lines in the Many-Worlds,
short strings representing
virtual particles and loops.
Step 8:
Fundamentally,
physics
is
described
on
HyperDiamond
Lattice
structures.
There are 7 independent E8 lattices, each corresponding to one of the 7 imaginary octionions. denoted by iE8, jE8, kE8, EE8, IE8, JE8, and KE8 and related to both D8 adjoint and half-spinor parts of E8 and with 240 first-shell vertices.
An 8th 8-dim lattice 1E8 with 240 first-shell vertices related to the E8 adjoint part of E8 is related to the 7 octonion imaginary lattices.
Give each D8
brane structure based on Planck-scale E8 lattices so that each D8
brane is a superposition/intersection/coincidence of the eight E8
lattices.
( see viXra 1301.0150v2 )
Step 9:
Since
Polchinski says
"... If r D-branes coincide ... there are r^2 vectors, forming the
adjoint
of a U(r) gauge group ...", make the
following
assignments:
¥
a
gauge boson emanating from D8 from its 1E8 and EE8 lattices is a U(2)
ElectroWeak boson thus accounting for the photon and W+, W- and Z0
bosons.
¥
a
gauge boson emanating from D8 from its IE8, JE8, and KE8 lattices is a
U(3)
Color Gluon boson thus accounting for the 8 Color Force Gluon bosons.
The 4+8 = 12
bosons of the Standard Model
Electroweak and Color forces correspond to 12 of the 28 dimensions of
28-dim Spin(8) that corresponds to the 28 of the
120-dim adjoint D8 part of E8.
¥
a
gauge boson emanating from D8 from its 1E8, iE8, jE8, and kE8 lattices
is a
U(2,2) boson for conformal U(2,2) = Spin(2,4)xU(1) MacDowell-Mansouri
gravity
plus conformal structures consistent with the Higgs mechanism and with
observed Dark Energy, Dark Matter, and Ordinary matter.
The 16-dim U(2,2) is a subgroup of 28-dim Spin(2,6) that
corresponds to
the 28 of the
120-dim adjoint
D8 part of E8.
Step 10:
Since
Polchinski says
"... there will also be r^2 massless scalars from the components normal
to
the D-brane. ... the collectives
coordinates ... X^u
... for the embedding of n D-branes in spacetime are now enlarged to
nxn
matrices. This 'noncummutative geometry' ...[may
be]... an
important hint about the nature of spacetime. ...", make the following assignment:
The 8x8
matrices for
the collective coordinates linking a D8 brane to the next D8 brane in
the stack
are needed to connect the eight E8 lattices of the D8 brane to the
eight E8
lattices of the next D8 brane in the stack.
The 8x8 = 64
correspond to the 64 of the 120
adjoint D8
part of E8.
We have now
accounted
for all the scalars
and
have shown
that the
model has the physics content of the realistic E8 Physics model
with
Lagrangian
structure based on E8 = (28
+ 28 + 64) + (64
+ 64)
and AQFT
structure
based on Cl(16) with real Clifford Algebra
periodicity
and generalized Hyperfinite II1 von Neumann factor algebra.
in which Strings are physically interpreted as World-Lines,
can be described by taking the quotient of its 24-dimensional O+, O-, Ov subspace
modulo the 24-dimensional Leech lattice.
Its automorphism group is the largest finite sporadic group, the Monster Group,
whose order is
8080, 17424, 79451, 28758, 86459, 90496, 17107, 57005, 75436, 80000, 00000
=
2^46 .3^20 .5^9 .7^6 .11^2 .13^3 .17.19.23.29.31.41.47.59.71
or about 8 x 10^53.
A Leech lattice construction is described by Robert A. Wilson in his
2009 paper
"Octonions and the Leech lattice":
"... The (real) octonion algebra is an 8-dimensional (non-division)
algebra with an orthonomal basis { 1=ioo , i0 , i1 , i2 , i3 , i4 , i5
, i6 } labeled
by the projective line PL(7) = { oo } u F7
...
The E8 root system embeds in this
algebra ... take the 240 roots to be ...
112 octonions ... +/- it +/- iu for
any distinct t,u
... and ...
128 octonions (1/2)( +/- 1 +/- i0 +/-
... +/- i6 ) which have an odd number of minus signs.
Denote by L the lattice spanned by
these 240 octonions
...
Let s = (1/2)( - 1 + i0 + ... + i6 ) so s is in L ... write R for Lbar
...
...
(1/2) ( 1 + i0 ) L = (1/2) R ( 1 + i0 ) is closed under multiplication
... Denote this ...by A
... Writing B = (1/2) ( 1 + i0 ) A ( 1 + i0 ) ...from ... Moufang laws
... we have
L R = 2 B , and ... B L = L and R B = R ...[ also ]... 2 B = L
sbar
...
the roots of B are
[ 16 octonions ]... +/- it for t
in PL(7)
... together with
[ 112 octonions ]... (1/2) ( +/- 1 +/-
it +/- i(t+1) +/- i(t+3) ) ...for t in F7
... and ...
[ 112 octonions ]... (1/2) ( +/-
i(t+2) +/- i(t+4) +/- i(t+5) +/- i(t+6) ) ...for t in F7
...
the octonionic Leech lattice ...
contains the following 196560 vectors of norm 4 ,
where M is a root of L and j,k are in J = { +/- it | t in PL(7) },
and all permutations of the three coordinates are allowed:
( 2 M, 0 , 0
)
Number:
3x240
=
720
( M sbar, +/- ( M sbar ) j , 0
) Number:
3x240 x 16 = 11520
( ( M s ) j , +/- M k , +/- (M j ) k
) Number: 3x240 x 16 x 16 = 184320
...
The key to the simple proofs above is the observation that LR = 2B and
BL = L:
these remarkable facts appear not to have been noticed before ...
some work ...
by Geoffrey Dixon ...". Geoffrey Dixon says in his book "Division
Algebras, Lattices, Physics, Windmill Tilting" using notation
{e0,e1,e2,e3,e4,e5,e6,e7} for the Octonion basis elements that
Robert A. Wilson denotes by {1=ioo,i0,i1,i2,i3,i4,i5 ,i6}
and I often denote by {1,i,j,k,E,I,J,K}: "...

(spans over integers) ...
Ξeven has 16+224 = 240 elements ... Ξodd has 112+128 = 240 elements ...
E8even does not close with respect to our given octonion multiplication
...[but]...
the set Ξeven[0-a], derived from Ξeven by replacing each occurrence of
e0 ... with ea,
and vice versa, is multiplicatively closed. ...".
Geoffrey Dixon's Ξeven corresponds to B
Geoffrey Dixon's Ξeven[0-a]
corresponds to the seven At
Geoffrey Dixon's Ξodd corresponds to L
Ignoring factors like 2 , j , k , and +/-1 the Leech lattice
structure is:
( L , 0 , 0
)
Number:
3x240
=
720
( B , B , 0
)
Number:
3x240
x
16 = 11520
( L s , L , L
)
Number:
3x240
x
16 x 16 = 184320
( Ξodd , 0 , 0
)
Number:
3x240
=
720
( Ξeven , Ξeven , 0
)
Number:
3x240
x
16 = 11520
( Ξodd s , Ξodd , Ξodd
)
Number:
3x240
x
16 x 16 = 184320
My view is that the E8 domain B is
fundamental
and the E8 domains L and L s are derived from it.
That view is based on analogy with the 4-dimensional 24-cell
and its dual 24-cell. Using Quaternionic coordinates {1,i,j,k}
the 24-cell of 4-space has one Superposition Vertex for each 16-region
of 4-space.
A Dual 24-cell gives a new Superposition Vertex at each edge of the
region.
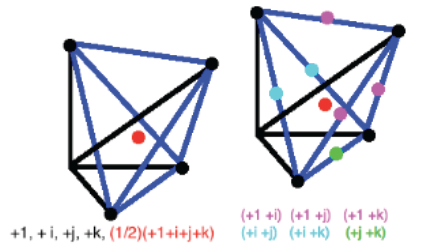
The Initial 24-cell Quantum Operators act with
respect to 4-dim Physical Spacetime.
{1,i,j,k} represent time and 3 space coordinates.
(1/2)(+1+i+j+k) represents
a fundamental first-generation Fermion particle/antiparticle (there is
one for for each of the 16-regions).
The Dual 24-cell Quantum Operators act with respect to 4-dim CP2
Internal Symmetry Space. Since CP2 = SU(3)/SU(2)xU(1),
(+1 +i) (+1 +j) (+1 +k)
are permuted by S3 to form the Weyl Group of Color Force SU(3),
(+i +j) (+i +k) are
permuted by S2 to form the Weyl Group of Weak Force SU(2),
(+j +k) is permuted by S1
to form the Weyl Group of Electromagnetic Force U(1).
The B-type 24-cell is fundamental because it gives Fundamental
Fermions.
The L-type dual 24-cell is derivative because it gives Standard Model
Gauge Bosons.
Robert A.Wilson in "Octonions and the Leech lattice" also said
"... B is not closed under
multiplication ... Kirmse's mistake
...[ but ]... as Coxeter ... pointed out ...
... there are seven non-associative
rings At = (1/2) ( 1 + it ) B ( 1 + it ) ,
obtained from B by swapping 1 with it
... for t in F7 ...".
H. S. M. Coxeter in "Integral Cayley Numbers" (Duke Math. J. 13 (1946)
561-578) said
"... Kirmse ... defines ... an integral domain ... which he calls J1
[Wilson's B] ...[but]...
J1 itself is not closed under multiplication ... Bruck sent ... a
revised description ...[of a]... domain J ... derived from J1 by
transposing two of the i's [imaginary Octonions]...
It is closed under multiplication ... there are ... seven such domains,
since the (7choose2) = 21 possible transpositions fall into 7 sets of
3, each set having the same effect. In each of the seven domains, one
of the ... seven i's ... plays a special role, viz., that one which is
not affected by any of the three transpositions. ...
J contains ... 240 units ... ". J is one of Wilson's seven At and, in
Octonionic coordinates {1,i,j,k,e,ie,je,ke}, is shown below with
physical interpretation color-coded as
8-dim Spacetime Coordinates x 8-dim Momentum Dirac Gammas
Gravity SU(2,2)=Spin(2,4) in a
D4 + Standard Model SU(3)xU(2) in a D4
8 First-Generation Fermion
Particles x 8 Coordinate Components
8 First-Generation Fermion
AntiParticles x 8 Coordinate Components
112 = (16+48=64) + (24+24=48) Root Vectors
corresponding to D8:
±1,
±i,
±j,
±k,
±e, ±ie, ±je, ±ke,
(±1
±i
±e
±ie
)/2
(±1
±j
±e
±je
)/2
(±1
±k
±e
±ke
)/2
(
±j
±k
±je
±ke
)/2
(
±i
±k
±ie
±ke
)/2
(
±i
±j
±ie
±je
)/2
128 = 64 + 64 Root Vectors corresponding to
half-spinor of D8:
(±1
±ie
±je
±ke
)/2
(±1
±j
±k
±ie
)/2
(±1
±i
±k
±je
)/2
(±1
±i
±j
±ke
)/2
(
±i
±j
±k
±e
)/2
(
±i
±e
±je
±ke
)/2
(
±j
±e
±ie
±ke
)/2
(
±k
±e
±ie
±je )/2
The above Coxeter-Bruck J is, in the notation I usually use, denoted
7E8 .
It is one of Coxeter's seven domains (Wilson's seven
{A0,A1,A2,A3,A4,A5,A6})
that I usually denote as { 1E8 , 2E8 , 3E8 , 4E8 , 5E8 , 6E8, 7E8 } .
Since the Leech lattice structure is
( L , 0 , 0
)
Number:
3x240
=
720
( B , B , 0
)
Number:
3x240
x
16 = 11520
( L s , L , L
)
Number:
3x240
x
16 x 16 = 184320
if you replace the structural B with 7E8 and the Leech lattice
structure becomes
( L , 0 , 0
)
Number:
3x240
=
720
( 7E8 , 7E8 , 0
)
Number:
3x240
x
16 = 11520
( L s , L , L
)
Number:
3x240
x
16 x 16 = 184320
and the Leech lattice of E8 26-dim String Theory is the Superposition
of
8 Leech lattices based on each of { B , 1E8 , 2E8 , 3E8 , 4E8 , 5E8 ,
6E8, 7E8 }
just as the D8 branes of E8 26-dim String Theory are each the
Superposition of
the 8 domains { B , 1E8 , 2E8 , 3E8 , 4E8 , 5E8 , 6E8, 7E8 } .
The full
26-dimensional Lattice Bosonic String Theory can be regarded as
an infinite-dimensional Affinization of the Theory of a Single Cell.
James
Lepowsky said in
math.QA/0706.4072:
"... the Fischer-Griess
Monster M ... was
constructed by Griess as a symmetry group (of order about 10^54) of a
remarkable new commutative but very, very highly nonassociative,
seemingly
ad-hoc, algebra B of dimension 196,883. The "structure constants"
of the Griess algebra B were "forced" by expected properties of the
conjectured-to-exist Monster. It was proved by J. Tits that M is
actually the
full symmetry group of B. ...
There should
exist a
(natural) infinite-dimensional Z-graded module for M (i.e.,
representation of
M)
V
= DIRSUM(n=-1,0,1,2,3,...) V_n ...
such
that
...
the graded dimension of the graded vector
space V ...
= ... SUM(n=-1,0,1,2,3,...) ( dim V_n ) q^n
where
J(q)
= q^(-1) + 0 + 196884q + higher-order terms,
the
classical modular function with its constant term set to 0. J(q)
is the suitably normalized generator of the field of SL(2, Z)-modular
invariant
functions on the upper half-plane, with q = exp( 2 pi i tau ) , tau in
the
upper half-plane ...
Conway and
Norton
conjectured ... for every g in M (not just g = 1), the the generating
function
...
the graded trace of the action of g on the
graded
space V ... = ... SUM(n=-1,0,1,2,3,...) ( tr g | V_n ) q^n
should
be the analogous "Hauptmodul" for a suitable discrete subgroup of
SL(2,R), a subgroup having a fundamental "genus-zero property," so
that its associated field of modular-invariant functions has a single
generator
(a Hauptmodul) ... (... the graded dimension is of course the graded
trace of
the identity element g = 1.) The Conway-Norton conjecture subsumed a
remarkable
coincidence that had been noticed earlier - that the 15
primes giving rise to the genus-zero property ... are precisely
the primes dividing the order of the ... Monster ...
the
McKay-Thompson conjecture ... that there should exist a natural ...
infinite-dimensional Z-graded M-module V whose graded dimension is J(q)
... was
( constructively ) proved .... The graded traces of some, but not all,
of the
elements of the Monster - the elements of an important subgroup of M,
namely, a
certain involution centralizer involving the largest Conway sporadic
group Co1
- were consequences of the construction, and these graded traces were
indeed
(suitably) modular functions ... We called this V "the
moonshine module V[flat]"
...
The construction ... needed ... a natural
infinite-dimensional "affinization" of the Griess algebra B acting on
V[flat]
This
"affinization," which was part of the new
algebra of vertex operators, is analogous to, but more subtle than, the
notion
of affine Lie algebra ....
More precisely, the vertex operators were needed for a "commutative
affinization" of a certain natural 196884-dimensional enlargement B' of
B,
with an identity element (rather than a "zero" element) adjoined to
B. This enlargement B' naturally incorporated the Virasoro algebra -
the
central extension of the Lie algebra of formal vector fields on the
circle -
acting on V[flat] ...
The vertex
operators
were also needed for a natural "lifting" of Griess's action of M from
the finite-dimensional space B to the infinite-dimensional structure V[flat], including its algebra of vertex
operators and its
copy of the affinization of B'.
Thus the
Monster was
now realized as the symmetry group of a certain explicit "algebra of
vertex operators" based on an infinite-dimensional Z-graded structure
whose graded dimension is the modular function J(q).
Griess's
construction of B and of M acting on B was
a crucial guide for us, although we did not start by using his
construction;
rather, we recovered it, as a
finite-dimensional "slice" of a new infinite-dimensional construction
using vertex operator considerations. ...
The initally
strange-seeming finite-dimensional Griess algebra was now embedded in a
natural
new infinite-dimensional space on which a certain algebra of vertex
operators
acts ... At the same time, the Monster, a finite group, took on a new
appearance by now being understood in terms of a natural
infinite-dimensional
structure. ... the largest sporadic finite
simple
group, the Monster, was "really" infinite-dimensional ...
The
very-highly-nonassociative Griess algebra, or rather, from our
viewpoint, the
natural modification of the Griess algebra, with an identity element
adjoined,
coming from a "forced" copy the Virasoro algebra, became simply the
conformal-weight-two subspace of an algebra of vertex operators of a
certain
"shape." ...
the
constant term of J(q) is zero, and this choice of constant term, which
is not
uniquely determined by number-theoretic principles, is not traditional
in
number theory. It turned out that the vanishing of the constant term
... was
canonically "forced" by the requirement that the Monster should act
naturally on V[flat] and on an associated
algebra of
vertex operators.
This
vanishing of the
degree-zero subspace of V[flat] is actually
analogous
in a certain strong sense to the absence of vectors in the Leech
lattice of
square-length two; the Leech lattice is a distinguished rank-24 even
unimodular
(self-dual) lattice with no vectors of square-length two.
In addition,
this
vanishing of the degree-zero subspace of V[flat]
and
the
absence
of
square-length-two
elements
of the Leech lattice are in
turn
analogous to the absence of code-words of weight 4 in the Golay
error-correcting code, a distinguished self-dual binary linear code on
a
24-element set, with the lengths of all code-words divisible by 4. In
fact, the
Golay code was used in the original construction of the Leech lattice,
and the
Leech lattice was used in the construction of V[flat]
This was
actually to
be expected ... because it was well known that the automorphism groups
of both
the Golay code and the Leech lattice are (essentially) sporadic finite
simple
groups; the automorphism group of the Golay code is the Mathieu group
M24 and
the automorphism group of the Leech lattice is a double cover of the
Conway
group Co1 mentioned above, and both of these sporadic groups were well
known to
be involved in the Monster ... in a fundamental way....
The Golay
code is actually unique subject to its distinguishing
properties mentioned above ... and the
Leech lattice is unique subject to its distinguishing properties
mentioned
above ... Is V[flat]
unique? If so, unique subject to what? ... this uniqueness is an unsolved problem ...
V[flat]
came to be viewed in retrospect by string theorists as an inherently
string-theoretic structure: the "chiral algebra" underlying the
Z2-orbifold conformal field theory based on the Leech lattice.
The
string-theoretic geometry is this: One takes the torus that
is the quotient of 24-dimensional Euclidean space modulo the Leech
lattice,
and then one takes the quotient of this manifold by the "negation"
involution x -> -x, giving rise to an orbit space called an
"orbifold"&emdash;a manifold with, in
this case, a "conical" singularity. Then one takes the
"conformal field theory" (presuming that it exists mathematically)
based on this orbifold, and from this one forms a "string theory" in
two-dimensional space-time by compactifying a 26-dimensional "bosonic
string" on this 24-dimensional orbifold. The string vibrates in a
26-dimensional space, 24 dimensions of which are curled into this
24-dimensional orbifold ...
Borcherds
used ...
ideas, including his results on generalized Kac-Moody algebras, also
called
Borcherds algebras, together with certain ideas from string theory,
including
the "physical space" of a bosonic string along with the
"no-ghost theorem" ... to prove the remaining Conway-Norton
conjectures for the structure V[flat] ...
What had
remained to prove was ... that ... the conjugacy classes outside the
involution
centralizer - were indeed the desired Hauptmoduls ... He accomplished
this by
constructing a copy of his "Monster Lie algebra" from the
"physical space" associated with V[flat] enlarged to a
central-charge-26
vertex algebra closely related to the 26-dimensional bosonic-string
structure
mentioned above. He transported the known action of the Monster from V[flat] to this copy of the Monster Lie algebra,
and ... he
proved certain recursion formulas ... ... he succeeded in concluding
that all
the graded traces for V[flat] must coincide with the formal series for
the
Hauptmoduls ...
this
vertex operator algebra V[flat] has the following three simply-stated
properties ...
¥
(1) V[flat],
which is an irreducible module for itself ... , is its only irreducible
module,
up to equivalence ... every module for the vertex operator algebra V
[flat] is
completely reducible and is in particular a direct sum of copies of
itself.
Thus the vertex operator algebra V[flat]
has no more
representation theory than does a field! ( I
mean a
field in the sense of mathematics, not physics. Given a field, every
one of its
modules - called vector spaces, of course - is completely reducible and
is a
direct sum of copies of itself. )
¥
(2) dim
V[flat]_0 = 0. This corresponds to the zero constant term of J(q);
while the constant term of the classical modular function is
essentially
arbitrary, and is chosen to have certain values for certain classical
number-theoretic purposes, the constant term must be chosen to be zero
for the
purposes of moonshine and the moonshine module vertex operator algebra.
¥
(3) The
central charge of the canonical
Virasoro algebra in V[flat] is 24. "24" is
the "same 24" so basic in number theory, modular function theory,
etc. As mentioned above, this occurrence of 24 is also natural from the
point
of view of string theory.
These three
properties
are actually "smallness" properties in the sense of conformal field
theory and string theory. These properties allow one to say that V[flat] essentially defines the smallest possible
nontrivial
string theory ... ( These "smallness" properties essentially amount
to: "no nontrivial representation theory," "no nontrivial gauge
group," i.e., "no continuous symmetry," and "no nontrivial
monodromy"; this last condition actually refers to both the first and
third "smallness" properties.)
Conversely,
conjecturally ... V[flat] is the unique
vertex
operator algebra with these three "smallness" properties (up to
isomorphism). This conjecture ... remains unproved. It would be the
conformal-field-theoretic analogue of the uniqueness of the Leech
lattice in
sphere-packing theory and of the uniqueness of the Golay code in
error-correcting code theory ...
Proving this
uniqueness conjecture can be thought of as the "zeroth step" in the
program of classification of (reasonable classes of) conformal field
theories.
M. Tuite has related this conjecture to the genus-zero property in the
formulation of monstrous moonshine.
Up to this
conjecture,
then, we have the following remarkable characterization of the largest
sporadic
finite simple group: The Monster is the
automorphism group of the smallest nontrival string theory that
nature
allows ... Bosonic 26-dimensional
space-time ... "compactified" on 24 dimensions, using the orbifold
construction V[flat] ... or more
precisely, the
automorphism group of the vertex operator algebra with the canonical
"smallness" properties. ...
This
definition of the
Monster in terms of "smallness" properties of a
vertex operator algebra provides a remarkable motivation for the
definition of the precise notion of vertex (operator) algebra. The
discovery of
string theory (as a mathematical, even if not necessarily physical)
structure
sooner or later must lead naturally to the question of whether this
"smallest" possible nontrivial vertex operator algebra V . exists, and the
question of
what its symmetry group (which turns out to be the largest sproradic
finite
simple group) is.
And on the
other hand,
the classification of the the finite simple groups - a mathematical
problem of
the absolutely purest possible sort - leads naturally to the question
of what
natural structure the largest sporadic group is the symmetry group of;
the
answer entails the development of string theory and vertex operator
algebra
theory (and involves modular function theory and monstrous moonshine as
well).
The Monster,
a
singularly exceptional structure - in the same spirit that the Lie
algebra E8
is "exceptional," though M is far more "exceptional" than
E8 - helped lead to, and helps shape, the very general theory of vertex
operator algebras. (The exceptional nature of structures such as E8,
the Golay
code and the Leech lattice in fact played crucial roles in the
construction of V[flat] ...
V[flat]
is defined over the field of real numbers, and in fact over the field
of
rational numbers, in such a way that the Monster preserves the real and
in fact
rational structure, and that the Monster preserves a rational-valued
positive-definite symmetric bilinear form on this rational structure.
...
the
"orbifold" construction of V[flat] ...[has
been]... interpreted in terms of algebraic quantum field theory,
specifically,
in terms of local conformal nets of von Neumann algebras on the circle
...
the
notion of vertex operator algebra is actually the
"one-complex-dimensional
analogue" of the notion of Lie algebra. But at the same time that it is
the "one-complex-dimensional analogue" of the notion of Lie algebra,
the notion of vertex operator algebra is also the "one-complex-
dimensional analogue" of the notion of commutative associative algebra
(which again is the corresponding "one-real-dimensional" notion). ...
This analogy with the notion of commutative associative algebra comes
from the
"commutativity" and "associativity" properties of the
vertex operators ... in a vertex operator algebra
...
The
remarkable and
paradoxical-sounding fact that the notion of vertex operator algebra
can be,
and is, the "one-complex-dimensional analogue" of BOTH the notion of
Lie algebra AND the notion of commutative associative algebra lies
behind much
of the richness of the whole theory, and of string theory and conformal
field
theory.
When
mathematicians
realized a long time ago that complex analysis was qualitatively
entirely
different from real analysis (because of the uniqueness of analytic
continuation, etc., etc.), a whole new point of view became possible.
In vertex
operator algebra theory and string theory, there is again a fundamental
passage
from "real" to "complex," this time leading from the
concepts of both Lie algebra and commutative associative algebra to the
concept
of vertex operator algebra and to its theory, and also leading from
point
particle theory to string theory. ...
While a
string sweeps
out a two-dimensional (or, as we've been mentioning,
one-complex-dimensional)
"worldsheet" in space-time, a
point particle of course sweeps out a one-real-dimensional
"world-line" in space-time, with time playing the role of the
"one real dimension," and this "one real dimension" is
related in spirit to the "one real dimension" of the classical
operads that I've briefly referred to - the classical operads
"mediating" the notion of associative algebra and also the notion of
Lie algebra (and indeed, any "classical" algebraic notion), and in
addition "mediating" the classical notion of braided tensor category.
The "sequence of operations performed one after the other" is related
(not perfectly, but at least in spirit) to the ordering
("time-ordering") of the real line.
But as we
have emphasized,
the "algebra" of vertex operator algebra theory and also of its
representation theory (vertex tensor categories, etc.) is "mediated"
by an (essentially) one-complex-dimensional
(analytic
partial) operad (or more precisely, as we have mentioned, the
infinite-dimensional analytic structure built on this). When one needs
to
compose vertex operators, or more generally, intertwining operators,
after the
formal variables are specialized to complex variables, one must choose
not
merely a (time-)ordered sequencing of them,
but
instead, a suitable complex number, or more generally, an analytic
local
coordinate as well, for each of the vertex operators.
This process,
very
familiar in string theory and conformal field theory, is a reflection
of how
the one-complex-dimensional operadic structure "mediates" the
algebraic operations in vertex operator algebra theory.
Correspondingly,
"algebraic"
operations
in
this
theory
are
not instrinsically
"time-ordered"; they are instead controlled intrinsically by the
one-complex-dimensional
operadic structure. The "algebra" becomes intrinsically geometric.
"Time," or
more precisely, as we discussed above,
the one-real-dimensional world-line, is
being replaced
by a one-complex-dimensional world-sheet.
This is the
case, too,
for the vertex tensor category structure on suitable module categories.
In
vertex operator algebra theory, "algebra" is more concerned with
one-complex-dimensional geometry than with one-real-dimensional time.
...".