Frank Dodd (Tony) Smith, Jr. - November
2011
Below the energy level of
ElectroWeak Symmetry Breaking
the Higgs mechanism gives mass to particles.
According to a Review on the Kobayashi-Maskawa mixing matrix by
Ceccucci, Ligeti, and Sakai in the 2010 Review of Particle Physics
(note that I have changed their terminology of CKM matrix to the
KM terminology that I prefer because I feel that it was Kobayashi
and Maskawa, not Cabibbo, who saw that 3x3 was the proper matrix
structure):
"... the charged-current W± interactions couple to the ...
quarks with couplings given by ...
Vud
Vus
Vub
Vcd
Vcs Vcb
Vtd
Vts Vtb
This Kobayashi-Maskawa (KM) matrix is a 3 × 3 unitary matrix.
It
can be parameterized by three mixing angles and the CP-violating KM
phase ...
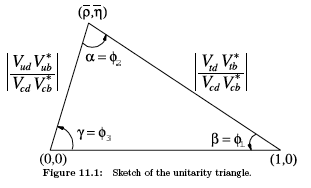
The most commonly used unitarity triangle arises from
Vud Vub∗ + Vcd Vcb∗ + Vtd Vtb∗ = 0, by dividing each
side by the
best-known one, Vcd Vcb∗
... ¯ρ + i¯η = −(Vud Vub∗)/(Vcd Vcb∗) is phase-convention-
independent ...
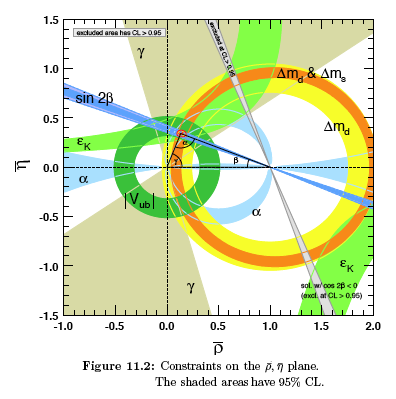
... sin 2β = 0.673 ± 0.023 ... α = 89.0 +4.4 −4.2 degrees
... γ = 73 +22 −25 degrees ...
The sum of the three angles of the unitarity triangle, α + β + γ = (183
+22 −25) degrees,
is ... consistent with the SM expectation. ...
The area... of ...[the]... triangle...[is]... half of the Jarlskog
invariant, J,
which is a phase-convention-independent measure of CP violation,
defined by Im Vij Vkl Vil∗ Vkj∗ = J SUM(m,n) ε_ikm
ε_jln
...
The fit results for the magnitudes of all nine KM elements are ...
0.97428 ±
0.00015
0.2253
±
0.0007
0.00347
+0.00016
−0.00012
0.2252 ±
0.0007
0.97345
+0.00015
−0.00016
0.0410
+0.0011
−0.0007
0.00862 +0.00026 −0.00020 0.0403
+0.0011−0.0007
0.999152 +0.000030−0.000045
and the Jarlskog invariant is J = (2.91 +0.19-0.11) × 10−5. ...".
Above the energy level of ElectroWeak
Symmetry Breaking particles are massless.
Kea (Marni Sheppeard) proposed that in the Massless Realm the mixing
matrix might be democratic.
In Z. Phys. C - Particles and Fields 45, 39-41 (1989) Koide said: "...
the mass matrix ... MD ... of the type ... 1/3 x m x
1 1 1
1 1 1
1 1 1
... has name... "democratic" family mixing ... the ... democratic ...
mass matrix can be diagonalized
by the transformation matrix A ...
1/sqrt(2)
-1/sqrt(2)
0
1/sqrt(6) 1/sqrt(6)
-2/sqrt(6)
1/sqrt(3)
1/sqrt(3) 1/sqrt(3)
as A MD At =
0 0 0
0 0 0
0 0 m
...".
Up in the Massless Realm you might just say that there is no mass
matrix,
just a democratic mixing matrix of the form 1/3 x
1 1 1
1 1 1
1 1 1
with no complex stuff and no CP violation in the Massless Realm.
When go down to our Massive Realm by ElectroWeak Symmetry Breaking
then you might as a first approximation use m = 1
so that all the mass first goes to the third generation as
0 0 0
0 0 0
0 0 1
which is physically like the Higgs being a T-Tbar quark condensate.
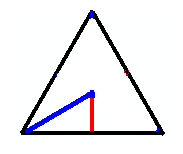
Consider a 3-dim Euclidean space of
generations:
The case of mass only going to one generation
can be represented as a line or 1-dimensional simplex
in which the blue mass-line covers the entire black simplex line.
If mass only goes to one other generation
that can be represented by a red line extendng to a second dimension
forming a small blue-red-black triangle
that can be extended by reflection to form six small triangles
making up a large triangle.
Each of the six component triangles has 30-60-90 angle structure:
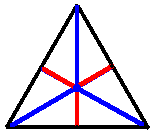
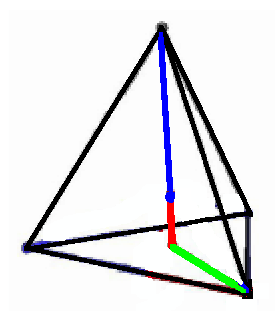
If mass goes on further to all three generations
that can be represented by a green line extending to a third dimension
If you move the blue line from the top vertex to join the green vertex
you get a small blue-red-green-gray-gray-gray tetrahedron
that can be extended by reflection to form 24 small tetrahedra
making up a large tetrahedron.
Reflection among the 24 small tetrahedra corresponds
to the 12+12 = 24 elements of the Binary Tetrahedral Group.
The basic blue-red-green triangle of the basic small tetrahedron
has the angle structure of the K-M Unitary Triangle.
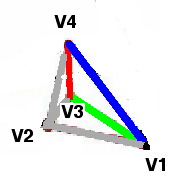
Using data from R. W. Gray's "Encyclopedia Polyhedra: A Quantum Module"
with lengths
V1.V2 = (1/2 ) EL ≡ Half of the regular Tetrahedron's edge length.
V1.V3 = ( 1 / sqrt(3) ) EL ≅ 0.577 350
269 EL
V1.V4 = 3 / ( 2 sqrt(6) ) EL ≅ 0.612
372 436 EL
V2.V3 = 1 / ( 2 sqrt(3) ) EL ≅ 0.288 675 135 EL
V2.V4 = 1 / ( 2 sqrt(2) ) EL ≅ 0.353 553 391 EL
V3.V4 = 1 / ( 2 sqrt(6) ) EL ≅ 0.204
124 145 EL
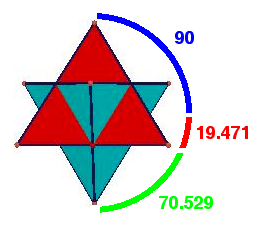
the Unitarity Triangle angles are:
β = V3.V1.V4 = arccos( 2 sqrt(2) / 3
) ≅ 19.471 220 634 degrees so sin 2β = 0.6285
α = V1.V3.V4 = 90 degrees
γ = V1.V4.V3 = arcsin( 2 sqrt(2) / 3
) ≅ 70.528 779 366 degrees
which is substantially consistent with the 2010 Review of Particle
Properties
sin 2β = 0.673 ± 0.023 so β = 21.1495 degrees
α = 89.0 +4.4 −4.2 degrees
γ = 73 +22 −25 degrees
and so also consistent with the Standard Model expectation.
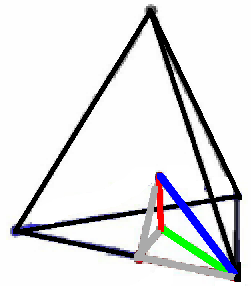
The constructed Unitarity Triangle angles can be seen on the Stella
Octangula
configuration of two dual tetrahedra (image from
gauss.math.nthu.edu.tw):
In my E8 Physics model the Kobayashi-Maskawa parameters are determined
in terms of
the sum of the masses of the 30 first-generation fermion particles and
antiparticles,
denoted by
Smf1 = 7.508 GeV,
and the similar sums for second-generation and third-generation
fermions,
denoted
by Smf2 = 32.94504 GeV and Smf3 = 1,629.2675 GeV.
The reason for using sums of all fermion masses (rather than sums of
quark masses
only) is that all fermions are in the same spinor representation of
Spin(8), and the
Spin(8) representations are considered to be fundamental.
The following formulas use the above masses to calculate
Kobayashi-Maskawa
parameters:
phase angle d13 = gamma = 70.529 degrees
sin(theta12) = s12 = [me+3md+3mu]/sqrt([me^2+3md^2+3mu^2]+
+ [mmu^2+3ms^2+3mc^2]) = 0.222198
sin(theta13) = s13 = [me+3md+3mu]/sqrt([me^2+3md^2+3mu^2]+
+ [mtau^2+3mb^2+3mt^2]) = 0.004608
sin(*theta23 = [mmu+3ms+3mc]/sqrt([mtau^2+3mb^2+3mt^2]+
+ [mmu^2+3ms^2+3mc^2])
sin(theta23) = s23 = sin(*theta23) sqrt( Sigmaf2 / Sigmaf1 ) =
0.04234886
The factor sqrt( Smf2 /Smf1 ) appears in s23 because an s23 transition
is to the
second generation and not all the way to the first generation, so that
the end
product of an s23 transition has a greater available energy than s12 or
s13
transitions by a factor of Smf2 / Smf1 .
Since the width of a transition is proportional to the square of the
modulus of the
relevant KM entry and the width of an s23 transition has greater
available energy
than the s12 or s13 transitions by a factor of Smf2 / Smf1
the effective magnitude of the s23 terms in the KM entries is increased
by the
factor sqrt( Smf2 /Smf1 ) .
The Chau-Keung parameterization is used, as it allows the K-M matrix to
be
represented as the product of the following three 3x3 matrices:
1
0
0
0
cos(theta23)
sin(theta23)
0
-sin(theta23)
cos(theta23)
cos(theta13)
0
sin(theta13)exp(-i
d13)
0
1
0
-sin(theta13)exp(i
d13)
0
cos(theta13)
cos(theta12)
sin(theta12)
0
-sin(theta12)
cos(theta12)
0
0
0
1
The resulting Kobayashi-Maskawa parameters for W+ and W- charged weak
boson
processes, are:
d
s
b
u 0.975
0.222
0.00249
-0.00388i
c -0.222
-0.000161i 0.974
-0.0000365i
0.0423
t 0.00698 -0.00378i
-0.0418
-0.00086i
0.999
The matrix is labelled by either (u c t) input and (d s b) output, or,
as above, (d s b)
input and (u c t) output.
For Z0 neutral weak boson processes, which are suppressed by the GIM
mechanism of cancellation of virtual subprocesses, the matrix is
labelled by either
(u c t) input and (u'c't') output, or, as below, (d s b) input and
(d's'b') output:
d
s
b
d' 0.975
0.222
0.00249
-0.00388i
s' -0.222
-0.000161i 0.974
-0.0000365i
0.0423
b' 0.00698 -0.00378i
-0.0418
-0.00086i
0.999
Since neutrinos of all three generations are massless at tree level,
the lepton sector
has no tree-level K-M mixing.