Here are some approaches from other points of view:
The E6-E7-E8 structures are based
on the Freudenthal-Tits Magic Square,
which shows relationships between
division algebras and matrix algebras.
In particular:
Division algebras define the rows of the Magic Square;
Jordan algebras define the columns of the Magic Square;
and
Lie algebras define the entries of the Magic Square.
The Jordan algebras are Hermitian matrices with
a symmetric product.
The Lie algebras are anti-Hermitian matrices with
an antisymmetric product.
The Magic Square includes ALL the exceptional Lie algebras,
but only some of the A, B, C, and D series Lie algebras.
There don't seem to be many references in standard textbooks.
I first read about it in
the article Jordan Algebras and their Applications,
by Kevin McCrimmon, Bull. AMS 84 (1978) 612-627, at pp. 620-621
and in
the unpublished 1976 Caltech notes of Pierre Ramond,
who I think learned about it from Feza Gursey at Yale.
Freudenthal wrote about it in Adv. Math. 1 (1964) 143, and
Tits in Indag. Math. 28 (1966) 223-237.
It is: (here I use Q for quaternion, and I follow McCrimmon
except that I correct a misprint of A6 that should (I think) be D6,
and I will also say that McCrimmon writes it as 4x5 instead of 4x4,
so that it is rectangle instead of square - other authors omit
the first column of McCrimmon's figure, and they get a 4x4 square,
but they don't have G2 as the derivation algebra of octonions O.)
R J3(R) J3(C) J3(Q) J3(O)
R 0 A1 A2 C3 F4
C 0 A2 A2+A2 A5 E6
Q A1 C3 A5 D6 E7
O G2 F4 E6 E7 E8
The columns are labelled
by Jordan algebras J = R, J3(R), J3(C), J3(Q), J3(O)
(where J3(K) is the algebra of 3x3 Hermitian matrices over K)
The rows are labelled
by composition algebras A = R, C, Q, O
It is a 4x5 rectangle, but the right 4 columns make a 4x4 square.
The 4x5 Magic Square entries are Lie algebras L formed
by the rule:
L = Der(A) + (A0xJ0) + Der(J)
where Der means derivation, + is direct sum, x is tensor product,
A0 are the pure imaginary elements of A, R0=S0, C0=S1, Q0=S3, O0=S7,
(here Sn means the algebra of tangent vectors to an n-dim sphere, and
S0,S1,S3 are Lie algebras and S7 is a Malcev algebra), and
J0 are the elements of trace zero of the Jordan algebra J.
(McCrimmon shows what the Lie products of such elements are,
on page 620 of his article in Bull. AMS).
Further, notice that
A1 is SU(2), A2 is SU(3), A5 is SU(6),
C3 is Sp(3) (denoted by some people Sp(6)),
D6 is SO(12) (same Lie algebra as Spin(12), and
G2, F4, E6, E7, and E8 are the exceptional Lie algebras.
The corresponding exceptional Lie groups are the subject
of the book Lectures on Exceptional Lie Groups by J. F. Adams,
published posthumously by Un. of Chicago Press in 1996,
edited by Zafer Mahmud and Mamoru Mimura.
To try to make the magic squares a little clearer,
here is the Magic Square with the dimensions
of the Lie algebras as entries:
R J3(R) J3(C) J3(Q) J3(O)
R 0 3 8 21 52
C 0 8 16 35 78=52+1x26
Q 3 21 35 66 133=52+3x26+3
O 14 52 78 133 248=52+7x26+14
R J3(R) J3(C) J3(Q)
R 0 3 8 21
C 0 8 16 35=21+1x14
Q 3 21 35 66=21+3x14+3
O 14 52 78 133=21+7x14+14
R J3(R) J3(C)
R 0 3 8
C 0 8 16=8+1x8
Q 3 21 35=8+3x8+3
O 14 52 78=8+7x8+14
R J3(R)
R 0 3
C 0 8=3+1x5
Q 3 21=3+3x5+3
O 14 52=3+7x5+14
To help a little more, consider the dimension of
3x3 matrices with entries Aij such that Aij = Aji*
(where * denotes conjugate)
If the entries of Aij are of dimension k
then the diagonal Aii are real, and
the matrix dimension is 3k + 3,
and if trace = sum of diagonals = 0, the dimension is 3k + 2.
Therefore:
for reals: 3x1 + 2 = 5;
for complex: 3x2 + 2 = 8;
for quaternion: 3x4 + 2 = 14;
for octonion: 3x8 + 2 = 26.
As for the first column,
which is rectangle part, not really part of the 4x4 square:
R
R 0 (no imaginary part)
C 0 (imaginary part dissipates)
Q 3 (imaginary part stable) 3 is dim of SU(2)
O 14=7+7 (imaginary part expands) 14 is dim of G2
Geoffrey Dixon shows how to construct F4, E6, E7, and E8 from a slightly different point of view:
To get from Geoffrey Dixon's construction to my construction,
use the fibrations S7 = Spin(8) / Spin(7) and S7 = Spin(7) / G2
to break the 28 of Spin(8) into 14 + 7 + 7 of G2, S7, and S7,
and add the two 7's to his 3x7, 6x7, 12x7, and 24x7
to get my 5x7, 8x7, 14x7, and 26x7.
John Baez writes This Weeks Finds in Math Physics on the WWW. His Week 64 describes E6; his Week 90 describes E8; and his Week 91 describes triality. The Freudenthal-Tits Magic Square can be formulated in the terms of his description of E8: Start with D4 = Spin(8): 28 = 28 + 0 + 0 + 0 + 0 + 0 + 0 Add spinors and vector to get F4: 52 = 28 + 8 + 8 + 8 + 0 + 0 + 0 Now, "complexify" the 8+8+8 part of F4 to get E6: 78 = 28 + 16 + 16 + 16 + 1 + 0 + 1 Then, "quaternionify" the 8+8+8 part of F4 to get E7: 133 = 28 + 32 + 32 + 32 + 3 + 3 + 3 Finally, "octonionify" the 8+8+8 part of F4 to get E8: 248 = 28 + 64 + 64 + 64 + 7 + 14 + 7 This way shows you that the "second" Spin(8) in E8 breaks down as 28 = 7 + 14 + 7 which is globally like two 7-spheres and a G2, one S7 for left-action, one for right-action, and a G2 automorphism group of octonions that is needed to for "compatibility" of the two S7s. the 3+3+3 of E7, the 1+0+1 of E6, and the 0+0+0 of F4 and D4 are the quaternionic, complex, and real analogues of the 7+14+7.
In MAGIC SQUARES OF LIE ALGEBRAS, math.RA/0001083, C.H. Barton and A. Sudbery say: "... This paper is an investigation of the relation between Tit's magic square of Lie algebras and certain Lie algebras of 3 x 3 and 6 x 6 matrices with entries in alternative algebras. By reformulating Tit's definition in terms of trialities (a generalisation of derivations), we give a systematic explanation of the symmetry of the magic square. We show that when the columns of the magic square are labelled by the real division algebras and the rows by their split versions, then the rows can be interpreted as analogues of the matrix Lie algebras su(3), sl(3) and sp(6) defined for each division algebra. We also define another magic square based on 2 x 2 and 4 x 4 matrices and prove that it consists of various orthogonal or (in the split case) pseudo-orthogonal Lie algebras. ...
... Tits ... showed ... the so-called magic square of Lie algebras of 3 x 3 matrices whose complexifications are
R C H O R A1 A2 C3 F4 C A2 A2xA2 A5 E6 H C3 A5 B6 E7 O F4 E6 E7 E8
The striking properties of this square are (a) its symmetry and (b) the fact that four of the five exceptional Lie algebras occur in its last row. ... The fifth exceptional Lie algebra, G2, can be included by adding a extra row corresponding to the Jordan algebra R . ...
... most exceptional Lie algebras are related to the exceptional Jordan algebra of 3 x 3 hermitian matrices with entries from the octonions, O. ... this relation yields descriptions of certain real forms of the complex Lie algebras
In math.AG/9810140, J. M. Landsberg and Laurent Manivel say: "... This is the first paper in a series establishing new relations between the representation theory of complex simple Lie groups and the algebraic and differential geometry of their homogeneous varieties. In this paper we determine the varieties of linear spaces on rational homogeneous varieties, provide explicit geometric models for these spaces, and establish basic facts about the local differential geometry of rational homogeneous varieties. Let G be a complex simple Lie group, P a maximal parabolic subgroup. The space of lines on G / P in its minimal homogeneous embedding was determined ...[ by Cohen and Cooperstein ]... in terms of Lie incidence systems. There is a dichotomy between the cases for which the simple root associated to P is short or not: for non-short roots, the space of lines on G / P is G-homogeneous and can be described using ideas of Tits; for short roots, it is not G-homogeneous. ... We present a refinement of their result ... (for a parabolic subgroup P which does not need to be maximal), that each connected component of the space of lines consists of exactly two G-orbits. ... We explain how to determine the higher dimensional linear spaces associated to non-short roots using Tits methods. For short roots, we provide explicit descriptions of the spaces we study, especially in the exceptional cases where we use Cayley's octonions. In all cases, each connected component of the variety of linear spaces on a G / P is quasi-homogeneous; more precisely, it is the union of a finite number of G-orbits. ...
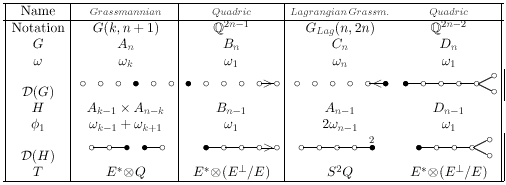
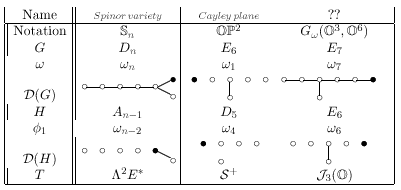
... Here is a table of the G-minuscule varieties: there are four infinite series and two exceptional spaces.


... Here E and Q are the tautological and quotient vector bundles on the Grassmannian or their pullbacks to the varieties in question. S+ is the half spin representation of D5, and J3(O) is the space of 3 x 3 O-Hermitian matrices, the representation V_w1 for E6 ... G_w( O3,O6 ) may be interpreted as the space of O3 's in O6 that are null for an O-Hermitian symplectic form ...
... As an algebraic variety, G2 / P1 is a familiar space, G2 / P1 = Q5 in P6 . ... G2 is not really an exceptional group, because it is defined by a generic form. ... The ... interpretation can be understood in terms of folding Dynkin diagrams:
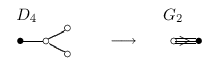
This indicates that G2 / P1 should be be understandable in terms of D4 / P1 = Q6 , and in fact it is a generic hyperplane section. Im O in O should be thought of as the traceless elements, where the trace of an element is its "real" part and we call the hyperplane section { tr = 0 } . ...
... J3(O) ... a Jordan algebra ... There is a well-defined determinant on J3(O ), which is defined by same expression as the classical determinant in terms of traces:
... F4 / P4 = OP2_0 . ... The description [of] ... F4 in GL(J3(O)) ... [as F4 = { g in E6 | g+ = g- } ... is motivated by folding of Dynkin diagrams:

... Note that F4 is generated by SO3 and Spin8 ... This defines an automorphism of the Jordan algebra J3( O)_0 because of the triality principle. ...
... E6 is the subgroup of GL( J 3(O )) = GL(27, C ) preserving det. The notion of rank one matrices is also well defined and the Cayley plane, E6 / P1 = OP2 in P(J3(O)) is the projectivization of the rank one elements, with ideal the 2 x 2 minors ... Since alpha_1 is not short, all linear spaces on OP2 are described by Tits geometries. In particular, E6/ P3 is the space of lines on OP2 and E6 / P2 is the space of P5 's on OP2 ...
In math.AG/9902102, J. M.Landsberg and Laurent Manivel say: "... Complex simple Lie algebras were classified by Cartan and Killing 100 years ago. Their proof proceeds by reducing the question to a combinatorical problem: the classification of irreducible root systems, and then performing the classification. We present a new proof of the classification via the projective geometry of homogeneous varieties. Our proof is constructive: we build a homogeneous space X in PN from a smaller space Y in Pn via a rational map Pn -> PN defined using the ideals of the secant and tangential varieties of Y. Our proof has three steps.
... Our proof can be translated into a combinatorical argument: the construction consists of two sets of rules for adding new nodes to marked Dynkin diagrams. As a combinatorical algorithm, it is less efficient than the standard proof ...
... minuscule representations define algebraic structures that are cousins of Clifford algebras ... the raising and lowering action corresponds to Clifford multiplication. ...
In math.AG/9908039, J. M.Landsberg and L. Manivel say: "... We connect the algebraic geometry and representation theory associated to Freudenthal's magic square. We give unified geometric descriptions of several classes of orbit closures, describing their hyperplane sections and desingularizations, and interpreting them in terms of composition algebras. In particular, we show how a class of invariant quartic polynomials can be viewed as generalizations of the classical discriminant of a cubic polynomial. ...
... Freudenthal associates to each group in the square a set of preferred homogeneous varieties (k-spaces for each group in the k-th row). These spaces have the same incidence relations with the corresponding varieties for the groups in the same row. He calls the geometries associated to the groups of the rows respectively, 2-dimensional elliptic, 2-dimensional plane projective, 5-dimensional symplectic and metasymplectic. The distinguished spaces are called respectively, spaces of points, lines, planes and symplecta. To avoid confusion, we will use the terminology F-points, F-planes etc. ... While Freudenthal was interested in the synthetic/axiomatic geometry of the spaces, we are primarily interested in the spaces as subvarieties of a projective space. ...
The Severi varieties ... the projective planes over the composition algebras ... have the unusual property that a generic hyperplane section of a Severi variety is still homogeneous. Putting the resulting varieties into a chart we have:
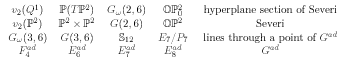
... These varieties are homogeneous spaces of groups whose associated Lie algebras are:
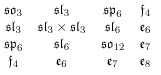
This chart is called Freudenthal's magic square of semi-simple Lie algebras.
The magic square was constructed by Freudenthal and Tits as follows: Let A denote a complex composition algebra (i.e. the complexification of R , C , the quaternions H or the octonions O ). For a pair ( A ; B ) of such composition algebras, the corresponding Lie algebra is
... To deduce the first line of the magic square from the second one we use the folding of a root system. ... Here is a chart summarizing the representations arising from folding:
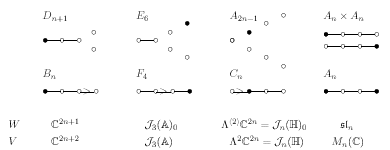
... the notations are explained ...[ in the paper ]...".
In math.AG/0107032, J. M.Landsberg and L. Manivel say: "... we thought it might be interesting to parametrize the exceptional series by a = dim CA , where A is respectively the complexification of 0, R, C, H, O for the last five algebras in the exceptional series (so a = 0, 1, 2, 4, 8). ... The construction we use highlights the triality principle, since we put a natural Lie algebra structure on the direct sum
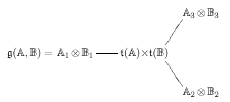
where t( A ) is a certain triality algebra associated to A . ... If A is a real Cayley algebra, it is a classical fact that T( A ) is an algebraic group of type D4. ... we get the following types for the Lie algebra t( A ) of T( A ) ...
t( R ) t( C ) t( H ) t( O ) 0 R2 so3 x so3 x so3 so8
... For B = O , our construction gives the last line of Freudenthal square. ... Consider the case of e8, i.e., A = O . ... Now we make a few observations on the weights of Ai. ... The weight structure is as follows:
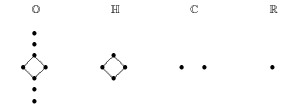
...".
Here are some more references: the book Nonassociative Algebras in Physics, by the Estonians Jaak Lohmus, Eugene Paal, and Leo Sorgsepp, Hadronic Press (1994) p. 58 and the book Division Algebras by Geoffrey Dixon, Kluwer (1994) chapter 8 and the article Division Algebras ... by A. Sudbery J. Phys. A: Math. Gen. 17 (1984) 939-955
......